有向图游戏与 SG 函数

有向图游戏是一个经典的博弈游戏——实际上，大部分的公平组合游戏都可以转换为有向图游戏。
在一个有向无环图中，只有一个起点，上面有一个棋子，两个玩家轮流沿着有向边推动棋子，不能走的玩家判负。

By : OI Wiki

mex 函数

$mex(S)$ ：不属于集合 S 的最小非负整数
例如 $mex(\{0, 1, 2, 4\}) = 3$ 、$mex(\emptyset) = 0$

SG 函数

对于状态 $x$ 和它的所有 $k$ 个后继状态 $y_1, y_2, \ldots, y_k$，定义 $\operatorname{SG}$ 函数：

$SG(x) = mex\{SG(y_1), SG(y_2), SG(y_3), ..., SG(y_k)\}$

什么时候结束游戏：
定义没有后继状态的为必败态，也就是 $\operatorname{SG}$函数为 $mex(\emptyset)$ 的状态，此时 $\operatorname{SG}$函数的值一定为 $0$

一个简单的巴什博弈问题：
有 $n$ 个石子，小 A 先取，小 B 后取，可以取一颗或者两颗石子，不能不取，最后取的人失败，两人都非常聪明，问谁获胜

Sameple Inpute --> 5

此问题符合对有向图游戏的定义

如果将每个状态视为一个节点，可以转化为一个博弈图

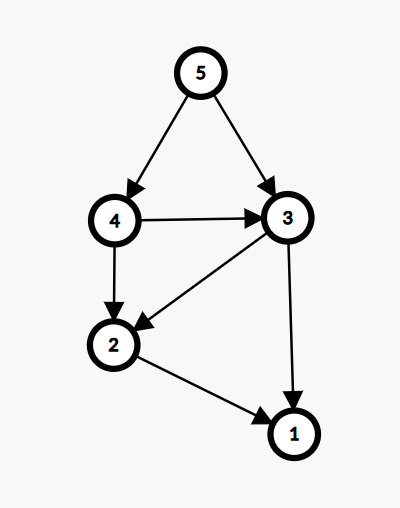
联系上方说过的对必败态的定义，$SG(1) = 0$

并且由此可以递归的得到所有点的 $SG$值

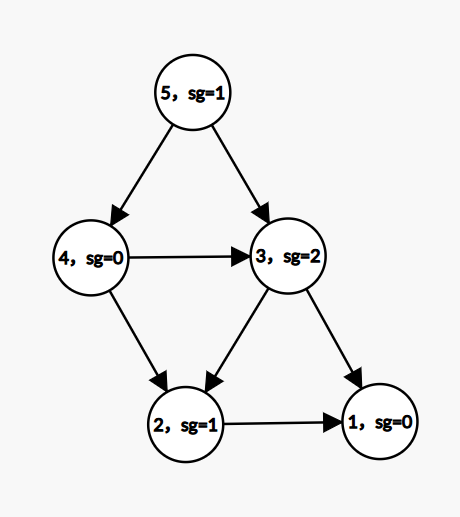
然后惊奇的发现，在这个博弈图中，$sg$ 等于 $0$ 时小A败， $sg$ 不等于 $0$ 时小A胜

推广一下，就是 $n$ 余 $3$ 不等于 $1$ 的时候小 A 胜，否则小 B 胜

if (n % 3 == 1) cout << B << endl;
else cout << A << endl;

链接：https://www.zhihu.com/question/445147447/answer/1740176817

其它例题
https://codeforces.com/contest/1033/problem/C

SG定理

定义

例题 >>> POJ2311 Cutting Game

参考：G60 有向图游戏 SG函数【博弈论】董晓
在这道题中，每次操作会造成两个状态，比如一个 4 * 3 的纸张可以被剪为 1 * 3 和 3 * 3 的、2 * 3 和 2 * 3的等状态

我们把每个 $a * b$ 的纸张看作一个节点，用 $(a, b)$ 表示
$SG$值被定义为 $SG((a, b)) = mex\{S_1, S_2, ..., S_k\}$
用 $S_i$ 来表示博弈图中 $(a, b)$ 子节点代表的$SG$值

$S_i = sg[x][b] \oplus sg[a - x][b]$ 或 $sg[a][y] \oplus sg[a][b - y] $

我们看到最先剪出 $(1, 1)$ 的人获胜，所以在本题中，将没有后继状态的 $(1, 1)$ 设置为必败态不合适
可以看出 $(1, n)$ 与 $(n, 1)$ 对于先取的人来说一定是必胜态
那么对应的，剪出 $(1, n)$ 与 $(n, 1)$ 的一定是必败态
所以本题中的必败态（也就是边界）设置为 $(2, 2)$、$(2, 3)$、$(3, 2)$、$(3, 3)$
因为这些状态一定能剪出必胜态
再递归的得到每个节点的$SG$值

点击查看代码

#include <bits/stdc++.h>

using namespace std;

void solve(int w, int h) {
    vector<vector<int>> sg(w + 1, vector<int> (h + 1, -1));

    sg[1][1] = 0;
    auto get = [&](auto self, int x, int y) {
        if (~sg[x][y]) return sg[x][y];

        set<int> S;

        for (int i = 2; i <= x - 2; i ++) {
            S.insert(self(self, i, y) ^ self(self, x - i, y));
        }

        for (int i = 2; i <= y - 2; i ++) {
            S.insert(self(self, x, i) ^ self(self, x, y - i));
        }

        for (int i = 0; ; i ++) {
            if (!S.count(i)) {
                return sg[x][y] = sg[y][x] = i;
            }
        }
    };

    cout << (get(get, w, h)? "WIN" : "LOSE") << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int w, h;
    while (cin >> w >> h) {
        solve(w, h);
    }

    return 0;
}

例题：CF768E
这个也是一道可以用sg函数来解决的题
我们很容易发现，给的数都小于60，并且这些堆的最多取的次数是一个可以计算出来的
具体来说，$(1 + k) \times k / 2 \leq x$，最大的 $k$ 就是 $x$ 能被取的最多的次数
每一堆的SG值是多少呢？
此时这道题转换为了一个朴素的nim游戏，可以证明 SG(x) = x

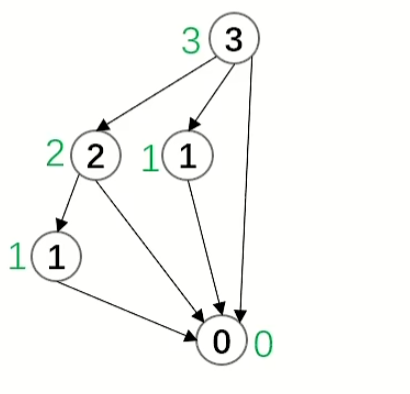
于是，可以将所有数异或起来，注意，此题问的后手必胜还是必败，若为0则胜，非0则败
因此，这道题其实就是一个nim游戏模板题，加上一点推导。

小凯取石子

参考

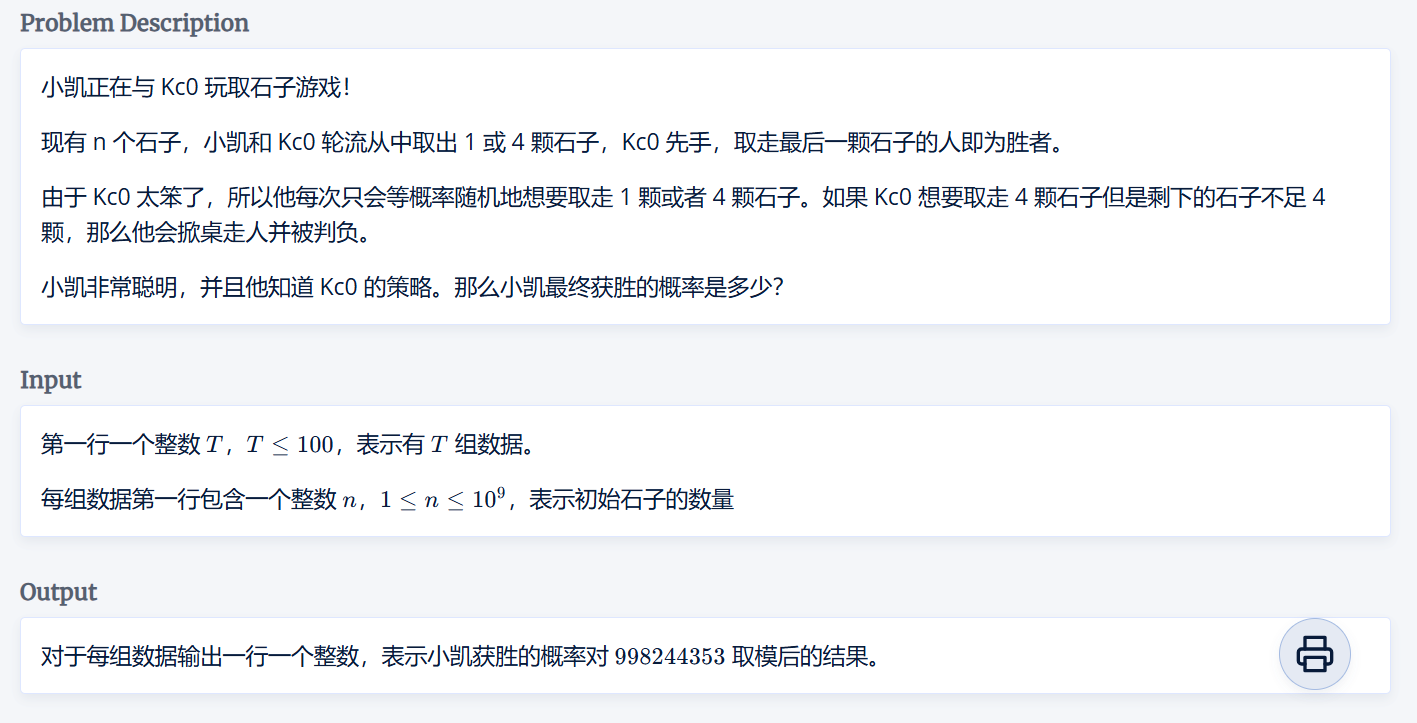
首先如果将概率之类的提问放到一边，计算只能取 $1$ 个或 $4$ 个，这种问题对应的 $sg$数
得到（从 $0$ 开始）： $0, 1, 0, 1, 2,| 0, 1, 0, 1, 2,| 0...$ （存在一个长度为 $5$ 的循环节）
可以假设Kc0取完 $1$ 个石子和取完 $4$ 个石子后，再计算答案
当$sg$值不为 $0$ 的时候，无论之后Kc0选什么小凯一定赢
依据这个，让$n$足够大再看 $n$%$5$ 各个值的情况
$n$%$5$$=0$ 从$1$和$4$来，一定为 $1$
$n$%$5$$=1$ 从$0$和$2$来，有$\frac{1}{2}$的概率一定赢，另外$\frac{1}{2}$由之前的概率递推来
$n$%$5$$=2$ 从$1$和$3$来，一定为 $1$
$n$%$5$$=3$ 从$2$和$4$来，有$\frac{1}{2}$的概率一定赢，另外$\frac{1}{2}$由之前的概率递推来
$n$%$5$$=4$ 从$0$和$3$来，有$\frac{1}{2}$的概率一定赢，另外$\frac{1}{2}$由之前的概率递推来

计算一到五小凯赢的概率 $P_1 = \frac{1}{2}$, $P_2 = 1$, $P_3 = \frac{3}{4}$, $P_4 = \frac{1}{4}$, $P_5 = 1$
之后可以推导出一个式子$P_i = \frac{1}{2} \times max(P_{i - 2}, P_{i - 5}) + \frac{1}{2} \times max(P_{i - 5}, P_{i - 8})$
然后经过推导与找规律，得到答案