Helga Hufflepuff's Cup CodeForces - 855C
Helga Hufflepuff's Cup CodeForces - 855C
题意：给一棵n个节点的树，要给每一个节点一个附加值，附加值可以为1-m中的一个整数。要求只能有最多x个节点有附加值k。如果某个节点的附加值是k，那么与其直接相连的点的附加值都必须小于k。求给整棵树的点赋附加值时满足要求的总方案数。
方法：
http://blog.csdn.net/ssimple_y/article/details/78081586
ans[i][j][k]表示以i节点为根的子树上选j个最高值且k满足条件（k=0表示i选比k小的值，k=1表示i选值为k，k=2表示i选比k大的值）时有多少种方法。显然，可以以任何一个节点为根开始dp。
对于每一个节点，计算其结果的方法要用一个小的dp。
t[i][j][p]表示（当前节点的）前i个子结点在情况p下选j个（p为0或1或2）的方案数。设第i子结点为xx。
在开始之前，由于即使一个子节点也不考虑，k=0,1,2时分别也有k-1,1,m-k种方法，也就是子节点的方案数还都要再分别乘以k-1,1,m-k，要先赋到t数组中。
$t[i][j][0]=sum\{t[i-1][j-y][0]*(ans[xx][y][0]+ans[xx][y][1]+ans[xx][y][2])\}$
$t[i][j][1]=sum\{t[i-1][j-y][1]*(ans[xx][y][0])\}$
$t[i][j][2]=sum\{t[i-1][j-y][2]*(ans[xx][y][0]+ans[xx][y][2])\}$
最后对于每个节点u，其ans[u][j][k]就等于t[u的子节点数量][j][k]。
当然，可以使用滚动数组优化t。
1 #include<cstdio> 2 #include<cstring> 3 #define md 1000000007 4 typedef long long LL; 5 struct Edge 6 { 7 LL to,next; 8 }edge[200100]; 9 LL k,m,n,x,anss; 10 LL f1[100100],n_e; 11 LL ans[100100][11][3]; 12 bool vis[100100]; 13 void m_e(LL a,LL b) 14 { 15 edge[++n_e].to=b; 16 edge[n_e].next=f1[a]; 17 f1[a]=n_e; 18 edge[++n_e].to=a; 19 edge[n_e].next=f1[b]; 20 f1[b]=n_e; 21 } 22 void dfs(LL u) 23 { 24 vis[u]=true; 25 LL kk,xx,j,q,ii=0; 26 LL t[2][11][3];//滚动数组 27 memset(t[0],0,sizeof(t[0])); 28 t[0][0][0]=k-1; 29 t[0][1][1]=1; 30 t[0][0][2]=m-k; 31 for(kk=f1[u];kk!=0;kk=edge[kk].next) 32 { 33 if(!vis[edge[kk].to]) 34 { 35 ii^=1; 36 memset(t[ii],0,sizeof(t[ii])); 37 xx=edge[kk].to; 38 dfs(xx); 39 memset(t[ii],0,sizeof(t[ii])); 40 for(j=0;j<=x;j++) 41 for(q=0;q<=x;q++) 42 { 43 if(j<q) break; 44 t[ii][j][0]=(t[ii][j][0]+t[ii^1][j-q][0]*(ans[xx][q][0]+ans[xx][q][1]+ans[xx][q][2]))%md; 45 t[ii][j][1]=(t[ii][j][1]+t[ii^1][j-q][1]*ans[xx][q][0])%md; 46 t[ii][j][2]=(t[ii][j][2]+t[ii^1][j-q][2]*(ans[xx][q][0]+ans[xx][q][2]))%md; 47 } 48 } 49 } 50 memcpy(ans[u],t[ii],sizeof(ans[u])); 51 } 52 int main() 53 { 54 LL a,b,i,j; 55 scanf("%I64d%I64d",&n,&m); 56 for(i=1;i<n;i++) 57 { 58 scanf("%I64d%I64d",&a,&b); 59 m_e(a,b); 60 } 61 scanf("%I64d%I64d",&k,&x); 62 dfs(1); 63 for(i=0;i<=x;i++) 64 for(j=0;j<3;j++) 65 anss=(anss+ans[1][i][j])%md; 66 printf("%I64d",anss); 67 return 0; 68 }
实际实现中，可以每计算完一个子节点的所有t值，就将其赋到ans[u]上，在计算下一个节点时，例如要访问t[i-1][j-y][2]，就相当于这种方法的ans[u][j-y][2]。这样可以避免每个子节点都要多开一个t数组。
1 #include<cstdio> 2 #include<cstring> 3 #define md 1000000007 4 typedef long long LL; 5 struct Edge 6 { 7 LL to,next; 8 }edge[200100]; 9 LL k,m,n,x,anss; 10 LL f1[100100],n_e; 11 LL ans[100100][11][3]; 12 LL t[11][3]; 13 bool vis[100100]; 14 void m_e(LL a,LL b) 15 { 16 edge[++n_e].to=b; 17 edge[n_e].next=f1[a]; 18 f1[a]=n_e; 19 edge[++n_e].to=a; 20 edge[n_e].next=f1[b]; 21 f1[b]=n_e; 22 } 23 void dfs(LL u) 24 { 25 vis[u]=true; 26 LL kk,xx,j,q; 27 ans[u][0][0]=k-1; 28 ans[u][1][1]=1; 29 ans[u][0][2]=m-k; 30 for(kk=f1[u];kk!=0;kk=edge[kk].next) 31 { 32 if(!vis[edge[kk].to]) 33 { 34 xx=edge[kk].to; 35 dfs(xx); 36 memset(t,0,sizeof(t)); 37 for(j=0;j<=x;j++) 38 for(q=0;q<=x;q++) 39 { 40 if(j<q) break; 41 t[j][0]=(t[j][0]+ans[u][j-q][0]*(ans[xx][q][0]+ans[xx][q][1]+ans[xx][q][2]))%md; 42 t[j][1]=(t[j][1]+ans[u][j-q][1]*ans[xx][q][0])%md; 43 t[j][2]=(t[j][2]+ans[u][j-q][2]*(ans[xx][q][0]+ans[xx][q][2]))%md; 44 } 45 for(j=0;j<=x;j++) 46 for(q=0;q<3;q++) 47 ans[u][j][q]=t[j][q]; 48 } 49 } 50 } 51 int main() 52 { 53 LL a,b,i,j; 54 scanf("%I64d%I64d",&n,&m); 55 for(i=1;i<n;i++) 56 { 57 scanf("%I64d%I64d",&a,&b); 58 m_e(a,b); 59 } 60 scanf("%I64d%I64d",&k,&x); 61 dfs(1); 62 for(i=0;i<=x;i++) 63 for(j=0;j<3;j++) 64 anss=(anss+ans[1][i][j])%md; 65 printf("%I64d",anss); 66 return 0; 67 }
错误记录：
（第二份代码）
曾经忘了写40行，导致数组越界访问WA。
曾经按照第一份代码的做，却没有每一次dfs单独开一个t数组，导致WA。
官方题解：
http://codeforces.com/blog/entry/54750
http://codeforces.com/blog/entry/54750?#comment-387718
This problem can be solved using precomputation of dp table dp[base][mask][len]. This stores the number of integers in base b and length len that forms the given mask in their representation. The mask is defined as having i - th bit as 1, if the digit i - 1 occurs odd number of times in the representation.
Using this precomputed dp array, we can easily calculate the answer for the queries, by converting l - 1 and r to the given base b, then adding the total integers less than equal to r with mask = 0 and subtracting those less than l with mask = 0.
Now, to find the number of integers less than equal to l - 1 with mask = 0, we first add all the integers with mask = 0 who have length less than length of l - 1 in base b representation. If length of l - 1 in base b is lb, this value can be calculated as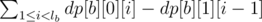 
. The second term is subtracted to take into account the trailing zeros.
Now, we need to calculate the number of integers with length = lb and value ≤ l - 1 and mask = 0. Let the number l - 1 in base brepresentation be l0, l1... llb. Then, if we fix the first digit of our answer, x from 0 to l0 - 1, we can simply calculate the mask for remaining digits we need as 2x and thus adding dp[b][2x][len - 1] to answer.
Now, if we fix the first digit as l0 only, we can simply perform the same operation for the second digit, selecting value of second digit, yfrom 0 to l1 - 1, and thus adding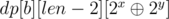 
to answer. And, we can move forward to rest of the digits in the same way.
The overall complexity of the solution will be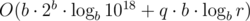 
let's say we want to calculate dp[v][j][x] (means the number of ways of getting x number of k type nodes in the subtree rooted at v, where type(v)=j) how to calculate this — let's assume f(v, j, x) has the same definition as dp[v][j][x].
say we have n children of node v. so essentially what we need to find is the number of ways to distribute x among these n children.
here we can use a dp. (for convenience I'll call nodes of type k as special node) Now, to do this computation at node v, we will form another DP dp1. We say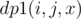 
as the number of ways to choose a total of x special nodes from subtrees defined by v1, v2, ..., vi i.e. from first i nodes. The recurrence can be defined as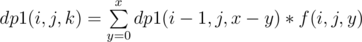 
, i.e. we are iterating over y assuming that subtree of vi contributes y special nodes and rest x-y special nodes have been contributed by previous i-1 nodes. So, finally dp[v][j][x] = dp1(n, j, x)
In the editorial solution this dp1 is denoted by a and b array. you wont find i in the editorial's dp1 state, i can be avoided by using two arrays a and b. we store dp1(i, , ) in b array, and after its calculation it is added to a array, so this will become dp1(i - 1, , ) for the next iteration.
