洛谷P4980 【模板】Polya定理
1、置换
置换简单来说就是对元素进行重排列,如下图所示。置换是[1,n]到[1,n]的一一映射。
举个直观的例子,将正方形绕其中心逆时针旋转90度,可以看成是正方形四个顶点的一个置换。关于置换、置换群的具体理论,请参考其他资料,此处有个大致印象就好。下面描述几个结论。
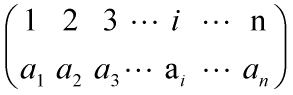
(1)置换可以分解成若干循环,方法为:连边1->a1,2->a2,…,i->ai,…,n->an,任取一个元素,顺着有向边走,直到回到出发点,即形成一个环,剩余元素如法炮制。
(2)如果一个状态经过置换 f 后跟原来相同,即S[1] = S[a1], S[2] = S[a2], …, S[n] = S[an]。则称该状态为 f 的不动点。
(3)题目中常常出现“本质不同的方案数”,一般是指等价类的数目,题目定义一个等价关系,满足等价关系的元素属于同一等价类。等价关系通常是一个置换集合F,如果一个置换能把其中一个方案映射到另一个方案,则二者是等价的。
2、burnside引理
对于一个置换f,若一个染色方案s经过置换后不变,称s为f的不动点。将f的不动点数目记为C(f),则可以证明等价类数目为所有C(f)的平均值。
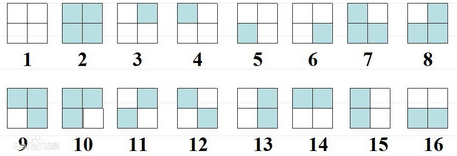
如上图(图片来自百度百科“burnside引理”)所示,对于四个置换{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°},其不动点数分别为16, 2, 4, 2。所以等价类数目为(16+2+4+2)/4 = 6。
3、polya定理
polay定理实际上是burnside引理的具体化,提供了计算不动点的具体方法。
假设一个置换有k个循环,易知每个循环对应的所有位置颜色需一致,而任意两个循环之间选什么颜色互不影响。因此,如果有m种可选颜色,则该置换对应的不动点个数为m^k。用其替换burnside引理中的C(f),得到等价类数目为:
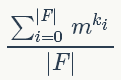
其中|F|表示置换的数目,ki表示第i个置换包含的循环个数。
对于此题,把染好色的环从某处断开看成一个序列,置换是:循环右移0位,循环右移1位,..,循环右移n-1位。(并不明白为什么要把循环右移0位放进去,先咕咕咕了)这样就使得同一个环染色方法的不同表示方法属于同一个等价类。
用burnside引理,得到等价类数目是对于各个置换的不动点数目的平均值。
就是,总的环染色方法数目$=\frac{\sum_{i=0}^{n-1}循环右移i位后不变的序列染色方法数目}{n}$。(把统计环染色方法数转化为统计序列染色方法数)
对于此题而言,置换分解成循环的实际操作举例:
循环右移0位分解成1(->1),2(->2),..,n(->n)这n个
循环右移1位分解成1->2->3->..->n(->1)这1个
循环右移2位,当n是奇数时分解成1->3->5->..->n->2->4->..->n-1(->1)这1个;当n是偶数时分解成1->3->5->..->n-1(->1),2->4->..->n(->2)这2个
......
可以发现,对于此题,循环右移i位的置换,可以分解成gcd(i,n)个循环
polya:一种序列染色方案a是置换A的不动点,那么A的同一个循环中的所有位置显然都需要有相同的颜色,A的不同循环中的位置的颜色互不影响,那么置换A的不动点个数就是颜色种类数的循环个数次方
因此此题最终答案是$\frac{\sum_{i=0}^{n-1}n^{gcd(i,n)}}{n}$
好像不能直接算,可以化简成$\frac{\sum_{j|n}n^j\varphi(\frac{n}{j})}{n}$,就可以算了
这个$\varphi$的话,可以发现对于每个n,会涉及的所有$\varphi(i)$都满足i是n的因子,而且根据线性筛的递推方法分解质因数后递归(记忆化)一下算仍然只会涉及到n的因子;也可以先线性筛一小部分,总之怎么搞都行
错误记录:calc_phi错了
卡常记录:
(不开优化时)将直接计算上限sqrt(x)换成每次判断i*i<=x会更快;
尽管是64位机子,把某一些特定的longlong换成int能快2/3;
似乎递归+记忆化算phi没有直接暴力算快

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 #include<cmath> 6 using namespace std; 7 #define fi first 8 #define se second 9 #define mp make_pair 10 #define pb push_back 11 typedef long long ll; 12 typedef unsigned long long ull; 13 int T,n,ans; 14 int prime[20011],len,phi[100011]; 15 char nprime[100011]; 16 const int md=1000000007; 17 ll poww(ll a,ll b) 18 { 19 ll ans=1; 20 for(;b;b>>=1,a=a*a%md) 21 if(b&1) 22 ans=ans*a%md; 23 return ans; 24 } 25 int calc_phi(int n) 26 { 27 if(n<=100000) return phi[n]; 28 int ans=n; 29 for(int i=1;i<=len&&prime[i]*prime[i]<=n;++i) 30 if(n%prime[i]==0) 31 { 32 ans-=ans/prime[i]; 33 while(n%prime[i]==0) n/=prime[i]; 34 } 35 if(n>1) ans-=ans/n; 36 return ans; 37 } 38 int calc(int x) 39 { 40 return poww(n,x)*calc_phi(n/x)%md; 41 } 42 int main() 43 { 44 int i,j; 45 phi[1]=1; 46 for(i=2;i<=100000;++i) 47 { 48 if(!nprime[i]) prime[++len]=i,phi[i]=i-1; 49 for(j=1;j<=len&&i*prime[j]<=100000;++j) 50 { 51 nprime[i*prime[j]]=1; 52 if(i%prime[j]==0) {phi[i*prime[j]]=phi[i]*prime[j];break;} 53 else phi[i*prime[j]]=phi[i]*(prime[j]-1); 54 } 55 } 56 scanf("%d",&T); 57 while(T--) 58 { 59 ans=0; 60 scanf("%d",&n); 61 for(i=1;i*i<n;++i) 62 if(n%i==0) 63 { 64 ans+=calc(i); 65 if(ans>=md) ans-=md; 66 ans+=calc(n/i); 67 if(ans>=md) ans-=md; 68 } 69 if(i*i==n) 70 { 71 ans+=calc(i); 72 if(ans>=md) ans-=md; 73 } 74 printf("%lld\n",ans*poww(n,md-2)%md); 75 } 76 return 0; 77 }
upd20190305
发现貌似不了解更完善的定义,在一些题目上会遇到奇怪的问题...
证明?先咕咕咕
来自wikipedia
在数学中,群是由一个集合以及一个二元运算所组成的,符合下述四个性质(称为“群公理”)的代数结构。这四个性质是封闭性、结合律、单位元和对于集合中所有元素存在逆元素。
在集合论中,一个集合的置换是从该集合映至自身的双射。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号