MobileNets总结

Google在2017年上半年发表了一篇关于可以运行在手机等移动设备上的神经网络结构——MobileNets。MobileNets是基于深度可分离卷积（depthwise separable convolution）而设计的轻量级深度神经网络。这文章也介绍了两个超参数可以很好的平衡延时与精度，这两个超参数可以使人更方便地选出自己想要的网络结构。MobileNets的结构能用在图片分类、人脸识别、目标检测等上面。论文的mxnet代码已经开源，tensorflow的相关代码也开源了。

深度可分离卷积（depthwise separable convolution）

在上一篇博客中——ShuffleNet总结中已经说明过卷积的计算了，与这里卷积相关计算有一点不同的是：这论文中长度为\(n\)方阵计算的复杂度直接设为\(n^2\)，而我在前一篇博客中设为\(n^3\)，实际上能优化到\(n^{2.376}\)，加上openmp等多核多线程技术，方阵计算复杂度为\(n^2\)是合理的。

论文中的主要的思想是将一个标准卷积（standard convolution）分解成两个卷积，一个是深度卷积（depthwise convolution），这个卷积应用在每一个输入通道上；另一个是\(1 \times 1\)的逐点卷积（pointwise convolution），这个卷积合并每一个深度卷积的输出。

分解

为什么标准卷积能分解，怎么分解？先来看下论文给出的分解方法。如图一所示：

图1 标准卷积的分解

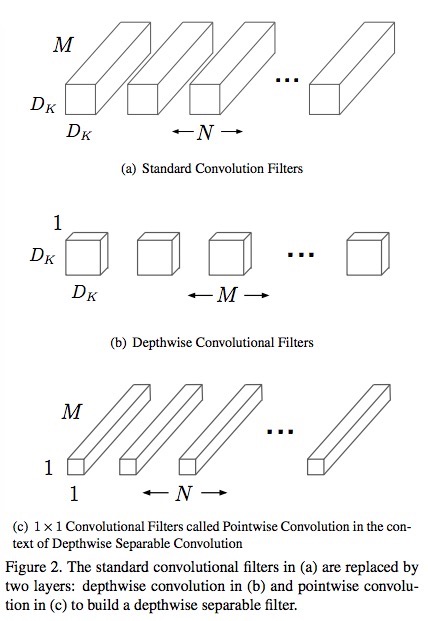
事实上标准卷积的分解可以用矩阵乘法来理解。在上一篇博客中——ShuffleNet总结卷积的计算时，如果卷积核\(K\)为\(D_K \times D_K \times M \times N\)，输入的\(D_F \times D_F \times M\)张量\(F\)（也叫Feature）,输出的\(D_F \times D_F \times N\)张量\(G\)（这里都采用了论文中的符号，\(D_K\)为卷积核的长与宽，\(M\)是是输入的通道数，\(N\)输出通道数，\(D_F\)是Feature的长与宽），先要将\(F\)转换成一个\((M \times D_K \times D_K) \times (D_F \times D_F)\)矩阵（就是im2col），卷积核\(K\)转换为\(N \times(M \times D_K \times D_K)\)。

卷积核这个矩阵可以分解成两个矩阵\(DW\)与\(PW\)的乘积，其中\({DW}\)代表depthwise convolution，\({PW}\)代表pointwise convolution。\(DW\)的shape为如图1b)所示的\(M \times (1 \times D_k \times D_k)\)，\(DP\)的shape为如图1c)所示的\(N \times (M \times 1 \times 1)\)，所以这两个相乘的shape刚好是卷积核\(K\)的shape：

\[K_{N \times(M \times D_K \times D_K)}={PW}_{N \times (M \times 1 \times 1)} \times {DW}_{M \times (1 \times D_k \times D_k)} \tag{1.1} \]

标准卷积计算

可以证明分解出来的两个卷积核与一个标准卷积核是等价的。标准卷积下的计算方法以下：

\[G_{N \times (D_F \times D_F)} = K_{N \times(M \times D_K \times D_K)} \times F_{(M \times D_K \times D_K) \times (D_F \times D_F)} \tag{1.2} \]

分解后的计算

分解成两个卷积后，先与第一个卷积核\(DW\)卷积，由于这个卷积核作用于每一个输入的通道，实现上就是分组了，一共分成了M组，这个需要循环计算M次：

\[{G1}_{M \times (D_F \times D_F)} = {DW}_{M \times(1 \times D_K \times D_K)} \times F_{(M/M \times D_K \times D_K) \times (D_F \times D_F)} \tag{1.3} \]

得到的\({G1}\)再转换成一个\((M \times 1 \times 1) \times (D_F \times D_F)\)矩阵\({G2}\)，再通过与\({PW}\)卷积可得：

\[{G3}_{N \times (D_F \times D_F)} = {PW}_{N \times(M \times 1 \times 1)} \times {G2}_{(M \times 1 \times 1) \times (D_F \times D_F)} \tag{1.4} \]

分解前后单元网络结构对比如图2所示：

图2 分解前后的对比图

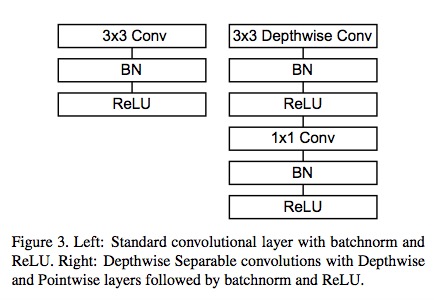
计算复杂度

对于标准卷积来说，根据式(1.2)可以看到计算量为：

\[Cost_{std} = D_K \times D_K \times M \times N \times D_F \times D_F \tag{1.5} \]

对于分解后的卷积，根据式(1.3)与式(1.4)可以看到计算量为：

\[Cost_{sep} = D_K \times D_K \times M \times D_F \times D_F + M \times N \times D_F \times D_F\tag{1.6} \]

分解前后的计算量之比是：

\[p = \frac{Cost_{sep}}{Cost_{std}} = \frac{1}{N} + \frac{1}{D_K^2} \tag{1.7} \]

可以看到前后的计算量是小了很多的。

MobileNets结构

经过上面的说明可以看得MoblieNets的结构如图3所示：

图3 MobileNets的网络结构

两个超参数

这两个超参数也是相当容易理解的，一个是减小输出通道数\(N\)，一个是减少输入图片的大小（退出是分辨率resolution）。

Width Multiplier \(\alpha\)

如果上面输出的通道数都是原来的\(\alpha\)倍，那么我们可以知道计算量由式(1.6)变为：

\[Cost_{sep}^\alpha = D_K \times D_K \times \alpha M \times D_F \times D_F + \alpha M \times \alpha N \times D_F \times D_F\tag{1.8} \]

由于\(D_K\)一般比\(N\)小很多，所以计算量与参数量都大约是\(\alpha =1\)（MobileNets的基准线）时的\(\alpha^2\)倍。\(\alpha\)一般取值为0.25，0.5，0.75和1。比如的结果如图4所示。

Resolution Multipliter \(\rho\)

这个用于控制输入图片的大小，输入的图片越小，后面的feature也会相于地变小，所以能减小计算量，但是并不能减小参数量，因为这个对于卷积核的大小没有影响，计算计算量由式(1.8)变为：

\[Cost_{sep}^{\alpha\rho} = D_K \times D_K \times \alpha M \times \rho D_F \times \rho D_F + \alpha M \times \alpha N \times \rho D_F \times \rho D_F\tag{1.9} \]

可以明显地看到，计算量为原来的\(\rho^2\)倍，如果以224大小为基准线，那么输入大小一般建议取为192、160与128。具体结果如图4所示。

图4 两个超参数对准确率、计算量与参数量的影响。

结语

MobileNets基以上面几种技术，训练出来的网络能很好地用于各类视觉任务，比如目标检测、分类等。

【防止爬虫转载而导致的格式问题——链接】：
http://www.cnblogs.com/heguanyou/p/8100246.html