OO第一单元总结 —— 多项式求导
OO第一单元总结 —— 多项式求导
一、代码分析
第一次作业
度量分析
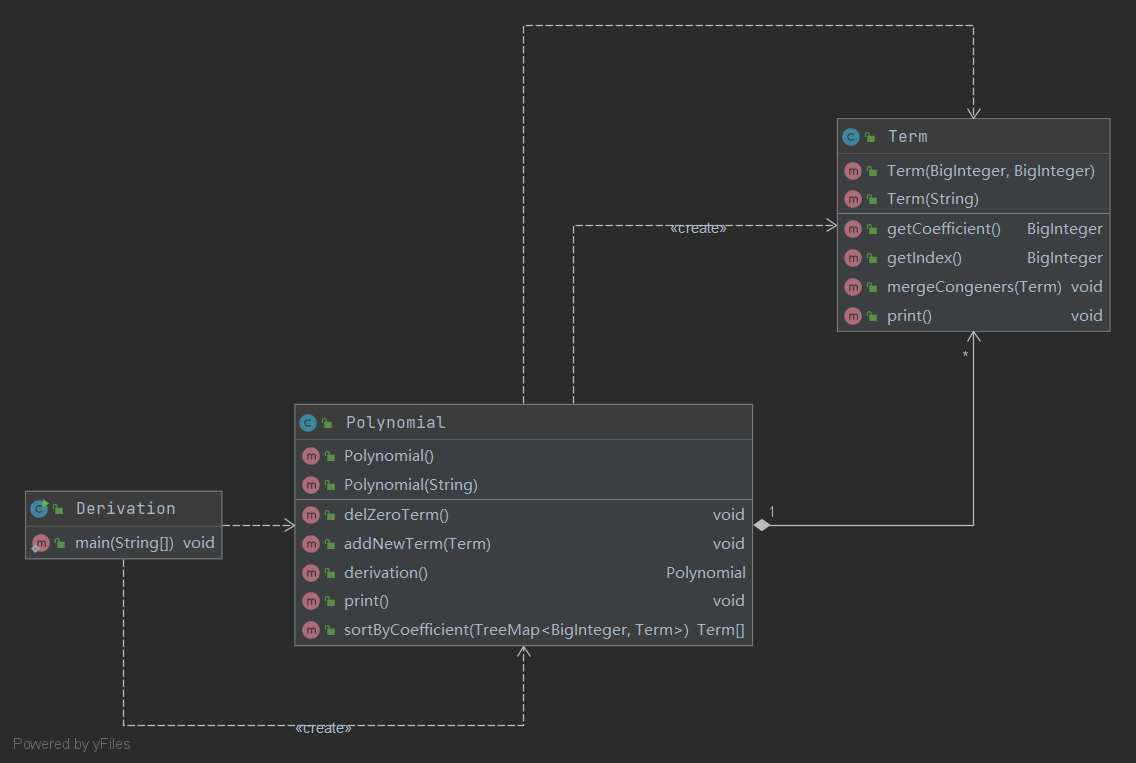
UML图
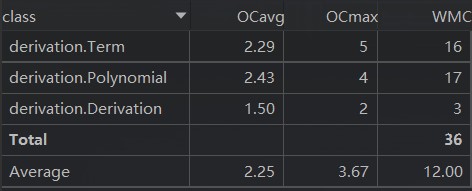
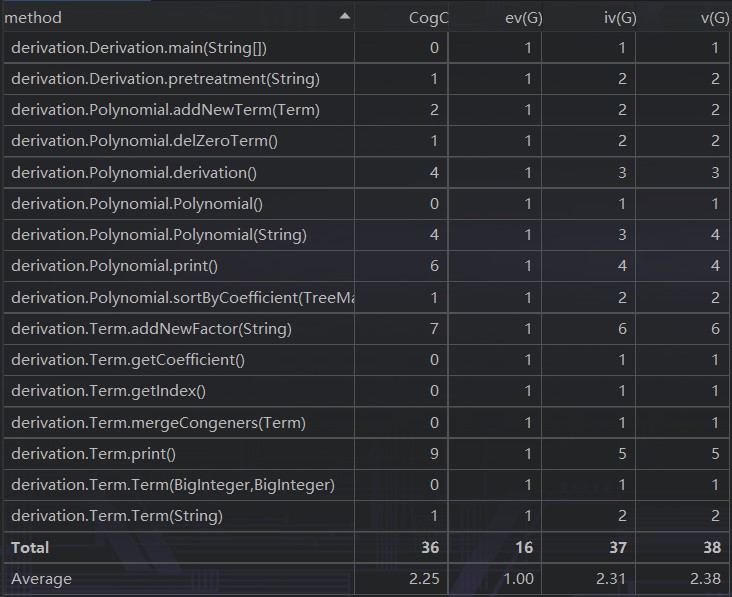
类与方法的复杂度
思路分析
程序主要包括以下五个步骤:
-
输入
从标准输入读入一行字符串,随后通过
pretreatment()函数进行初步处理,便于后续操作。处理过程全部通过
String类下的replace()方法实现,其主要操作有:消除空白字符
清除多余的
+和-(主要针对多个符号相连的情况)区分相同符号
连接因子的
*与表示指数的**(将后者替换为^)连接项的
-与其他位置的-(将后者替换为~)清除
*和^后面多余的+经过处理后,字符串内的
+和-均为连接项的符号,*均为连接项内因子的符号。 -
识别表达式
在经过之前的处理后,可以很容易的使用
String类下的split()函数将字符串拆解为因子,并将因子组合成的项储存在以指数为关键字的TreeMap中,同时自动完成了合并同类项的操作。 -
求导
通过循环操作对
TreeMap中的所有元素一一求导,并将结果添加到新的TreeMap中。采用和识别表达式时相同的方法,使得在完成求导的同时也完成了合并同类项的操作。
-
优化
本次作业中优化幅度最大的便是合并同类项的操作,已在求导的过程中实现。
除此之外,在逐项输出时,可以优先输出系数为正的项,从而有一定几率减少输出一个负号。
-
输出
循环逐项输出。
设计分析
本次作业中共使用了三个类:
-
Derivation
主类,负责数据的读入、控制程序按流程进行。
-
Polynomial
从多项式的层次对数据进行处理,主要包括识别、求导,以及合并同类项。
定义了一个
TreeMap用于存储项:private final TreeMap<BigInteger, Term> terms; -
Term
从项的层次对数据进行处理,主要包括项的识别和求导。
定义了两个
BigInteger变量分别用于保存项的系数和指数。
本次作业思路并不复杂,从上述统计数据可以看出程序结构也较为简单,但因为在编写程序时没有进行全面、深入地思考,最终编写的程序仍带有较明显的面向过程的特点,设计的三个类也几乎没有起到层次化的作用,只是简单地将一个面向过程的程序拆分到了三个文件里,这是此次作业中出现的最重要的问题。
其次,过度依赖于String类下的split()函数,借此绕开了十分生疏的正则表达式,即使到了第一单元的三次作业全部结束时也依旧如此,这部分知识有待后续加强学习。
BUG分析
整个过程中一共出现了两个较为严重的BUG
-
无法识别三个相连的
+或-公测中测找到的BUG
原因:在读完指导书后并没有想到三个符号居然可以连在一起ORZ,采用的以
replace和split为核心的数据处理方式也恰好无法处理这样的结构。下次一定120%认真读指导书 -
系数相同的项被吞掉
互测时被hack的BUG,其实在最后一次提交之后自己立刻就发现了,不过没时间改了QAQ
以后再也不压着DDL提交了为了实现“先输出正系数项以防止
-开头性能-1”而选择将所有项按系数重新排序逆序输出,却因过于激动选择了把所有项加入到一个以系数为关键字的TreeMap自动排序的方法,忽略了TreeMap不能存储键值相同的元素。这么严重的BUG强测居然也没测出来下次一定好好学习各类容器的用法
两个BUG都可以看做是逻辑问题,程序也较为简单,因而在复杂度方面没有太大差异。
第二次作业
度量分析
UML图
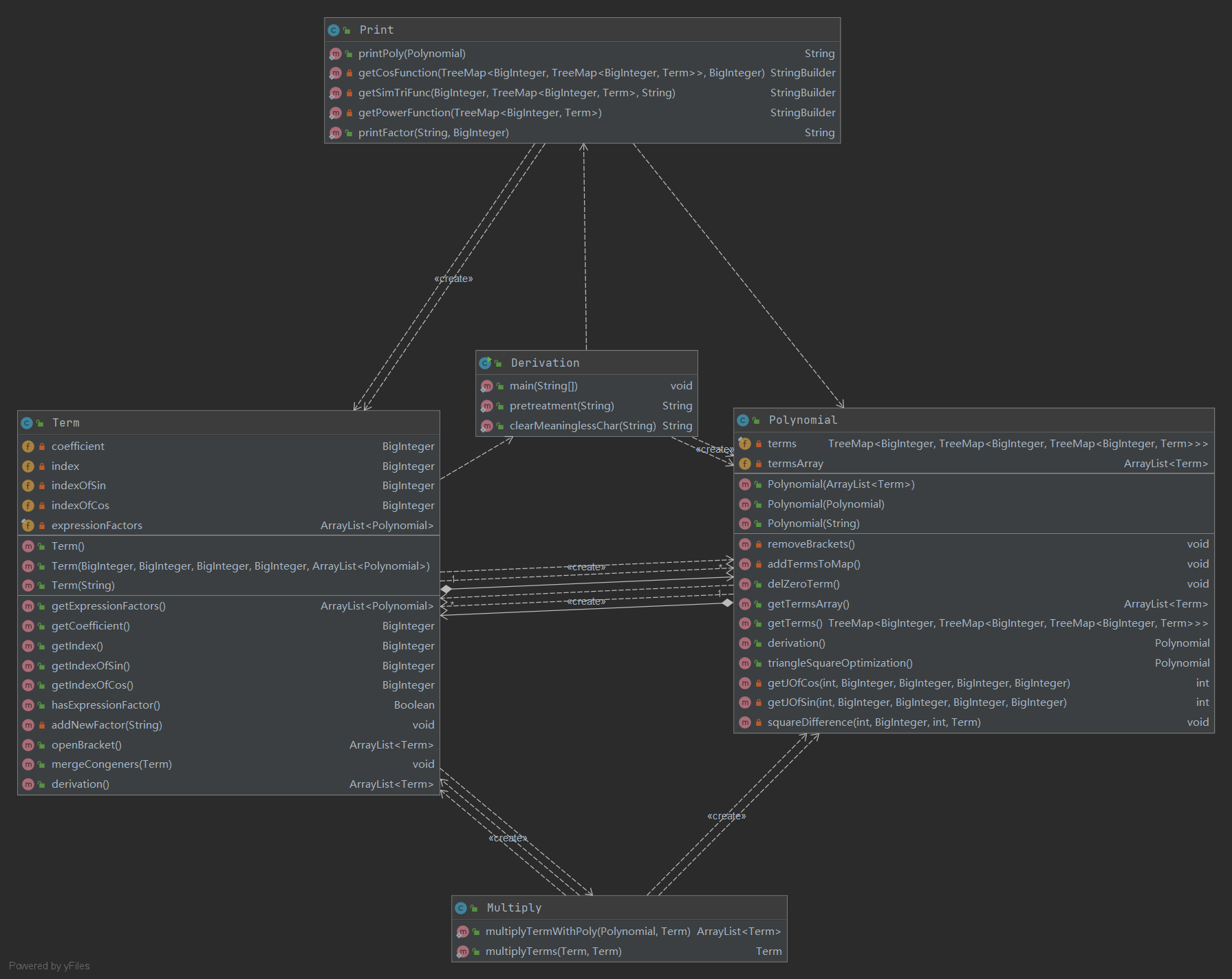
类与方法的复杂度
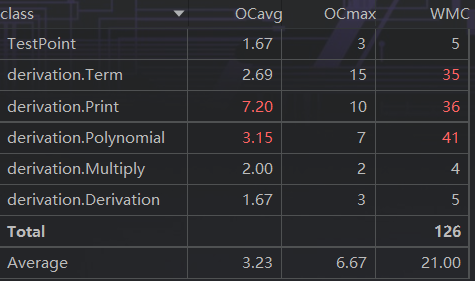
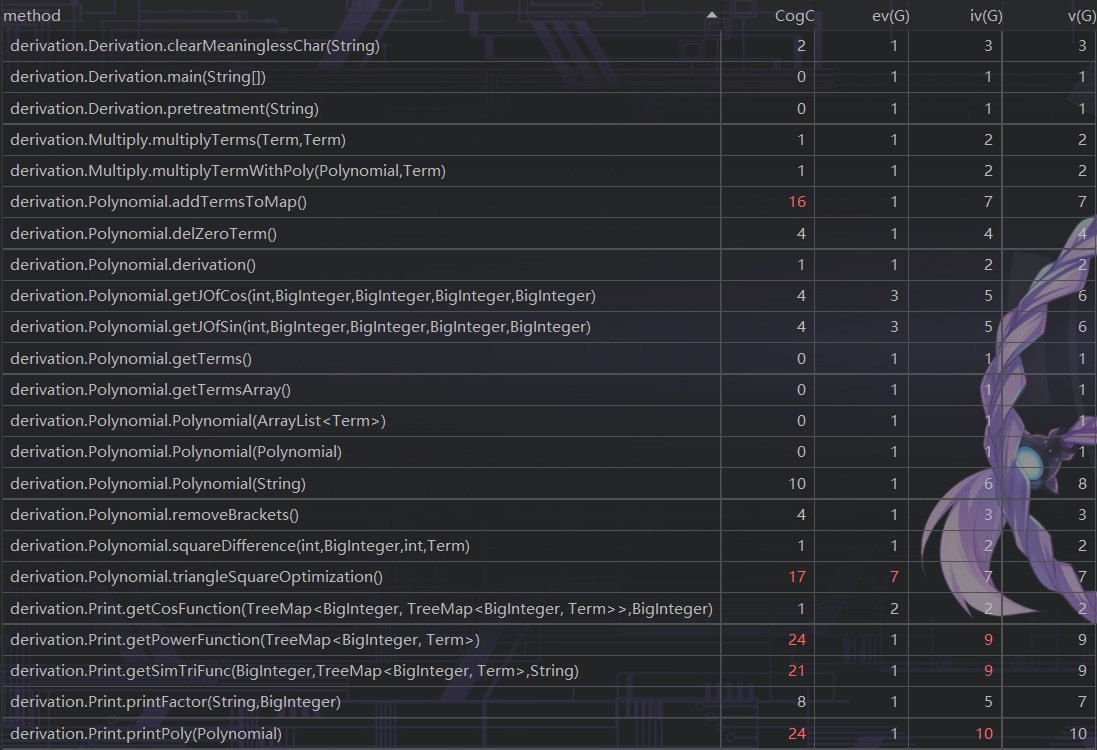
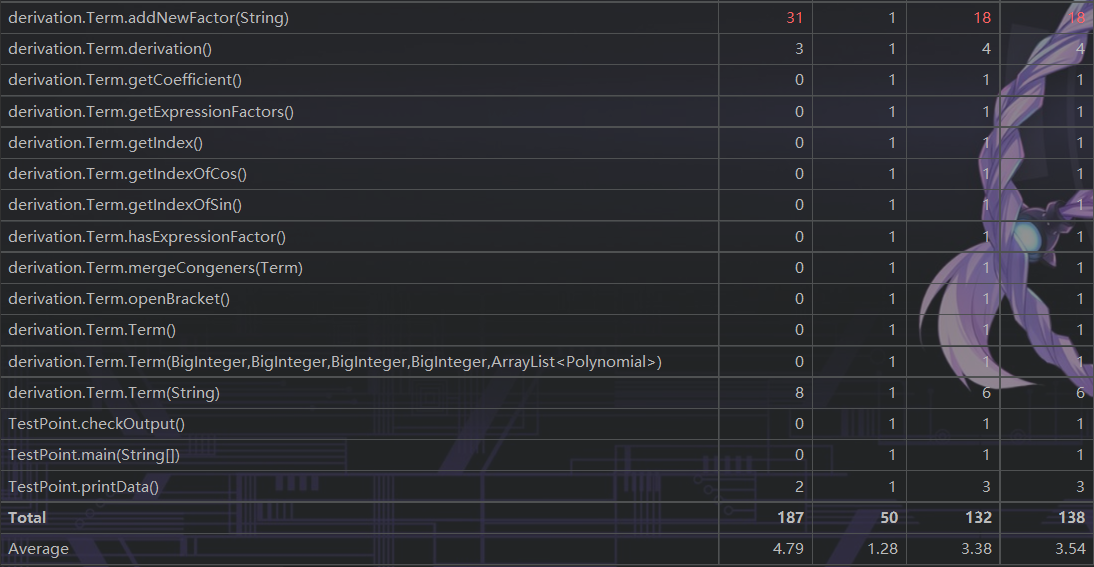
思路分析
程序依旧由第一次作业的五个步骤构成,只是为了适应新增的内容进行了部分调整。
-
输入
在预处理步骤中为了应对新情况进行了补充:
将
sin(x)和cos(x)分别替换为了s和c。去除了多项式首位和左括号后首位的
+。经过处理后,依旧满足字符串内的
+和-均为连接项的符号,*均为连接项内因子的符号,只不过新增了可以嵌套的表达式因子;此外,三角函数包含的括号已被消去,此时括号全部为表达式因子的标志。 -
识别表达式
放弃使用
String类下的split()函数,改为使用循环遍历进行拆分。拆项时对括号进行标记,将防止遇到表达式因子内部的
+或-将其错误地拆开。拆解因子时遇到括号便识别为表达式因子,进行递归识别,并将结果返回为一个多项式对象,存储在该项内定义的
ArrayList中。为了便于求导
因为懒得重写选择在识别结束后将括号全部打开,消除所有的表达式因子。 -
求导
加入了三角函数后,对每一个不同类型的因子依旧具有固定的求导方式。
对项进行求导时改为循环遍历每一个因子进行求导。
-
优化
增加了针对三角函数的平方和差的优化。
按照
sin、cos、幂函数的顺序组织三级TreeMap储存各项,并借此进行合并同类项等操作。 -
输出
循环逐项输出,增加了对超过两个元素的容器输出时加括号的判定。
设计分析
本次作业使用了五个类。
-
Derivation、Polynomial、Term
这三个类承担的功能不变,只是适应新的需求增添了部分方法。
调整了数据结构的设计:表达式中项的存储由单级
TreeMap改为了多级,关键字分别为sin、cos、和幂函数的指数:private final TreeMap<BigInteger, TreeMap<BigInteger, TreeMap<BigInteger, Term>>> terms; private ArrayList<Term> termsArray;同时为了适应后续操作,增加了一个便于直接遍历的
ArrayList。 -
Print
由五个静态方法构成,集中实现了对表达式的输出功能。
-
Multiply
由两个静态方法构成,主要负责进行项与项、项与多项式(表达式因子)之间的乘法。
在第二次作业中,因为懒得重构没有找到正确的方法,还是继续勉强地延续了第一次作业的整体结构与思路。
由于还陷在面向过程的编程思维中,虽然在识别表达式上没有遇到过多的阻碍,但在进行求导及组织数据结构时还是十分困难。从统计数据中也可以看出,几个数据并不十分美观的方法都集中在数据的存储和最后的输出上,复杂的数据结构所引起的复杂的逻辑最终还是成为了这种编程思维下无法忽视的困难。
此外,虽然本次作业中新增了两个类,但却并没有将面向对象编程的思维蕴含在内,只是将部分相似的功能简单的组合在了一起。现在看来。更应该做的是将Term类进行细化与拆分,并将字符串的判断识别作为统一的工厂类独立出来,而将乘法、输出等方法分别加入到各个类之中。
BUG分析
整个过程中出现了一个较为严重的BUG
-
输出结果加括号时出现"Format error"
按照预先设计的逻辑,遍历三级
TreeMap,当最高级只含有一个元素时不加括号,含有多个元素时用+或-连接并加括号;而另一方面,当最低级只含有一个常系数元素-1时,选择直接将符号提前,省略1*。if (item.size() == 1) { if (item.containsKey(BigInteger.ZERO)) { // sin(x)^n*(power function) TreeMap<BigInteger, Term> midItem = item.get(BigInteger.ZERO); sinFunc.append(getSimTriFunc(indexOfSin, midItem, "sin(x)")); } else { sinFunc.append(printFactor("sin(x)", indexOfSin)).append("*").append(getCosFunction(item, item.firstKey())); } }这就导致了在项的中间会出现
-cos(x)的格式错误。修改时没有过多考虑优化,选择对所有情况都加上括号,将其变为表达式因子。
从统计数据可以看出,出现BUG的位置恰好就是逻辑复杂、结构混乱的位置,而这些特点也确实加大了寻找问题的难度,但也正是这样的编程思路导致了如此繁琐的逻辑,从而增大了出现逻辑错误的几率。
第三次作业
UML图
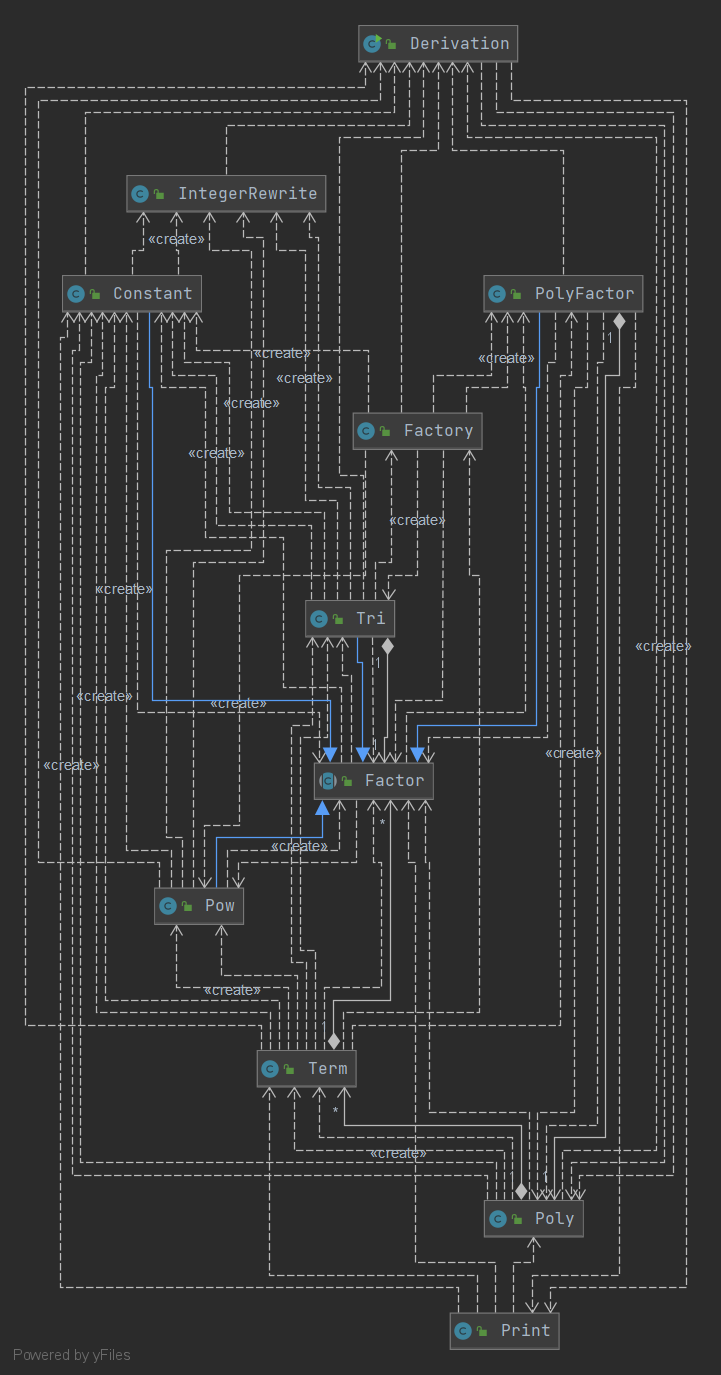
类与方法的复杂度
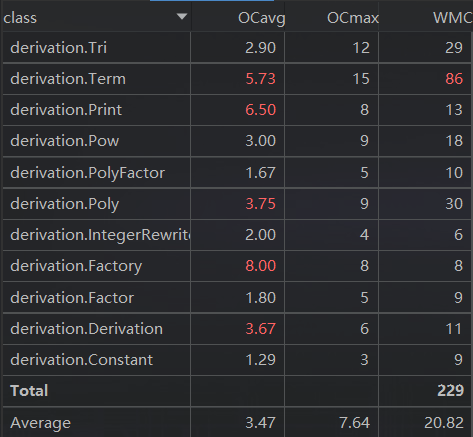
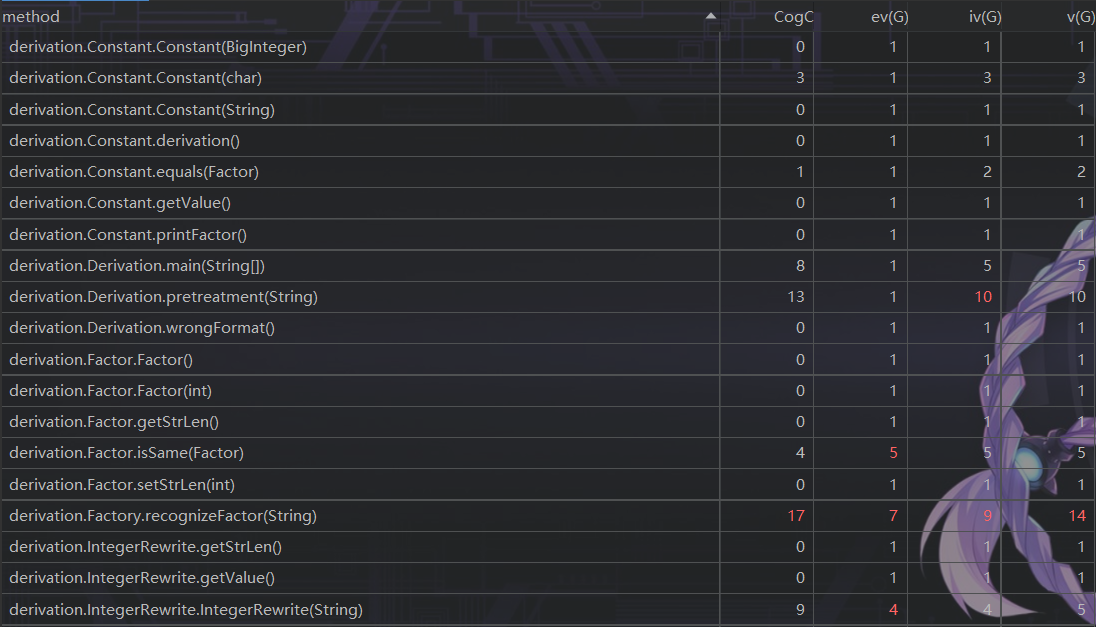
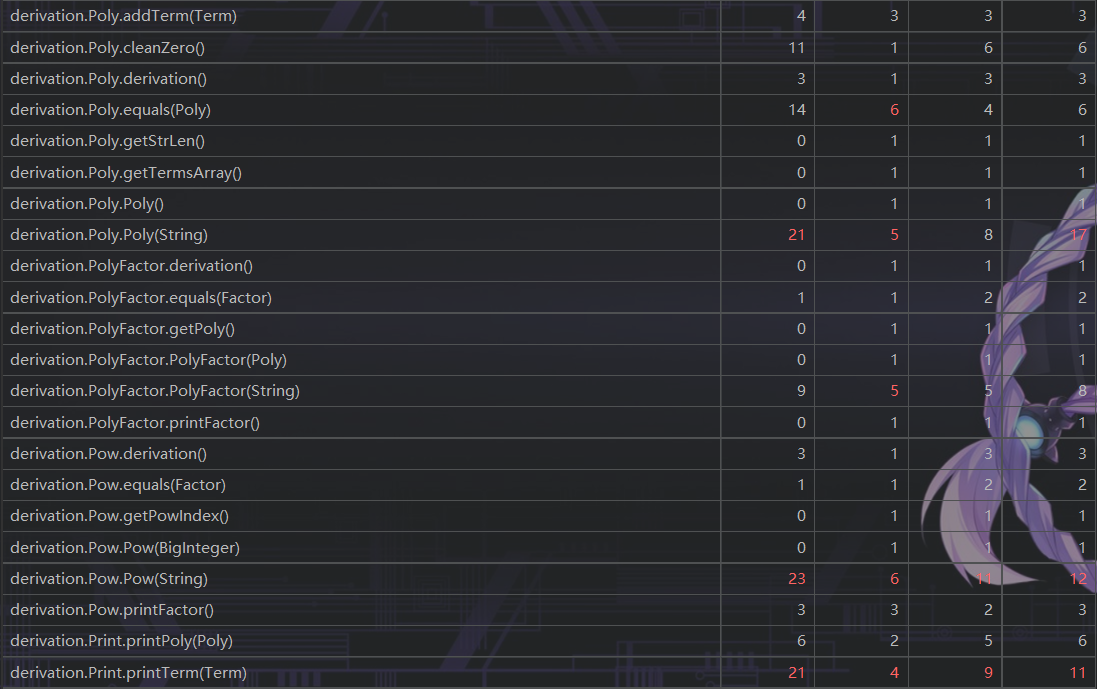
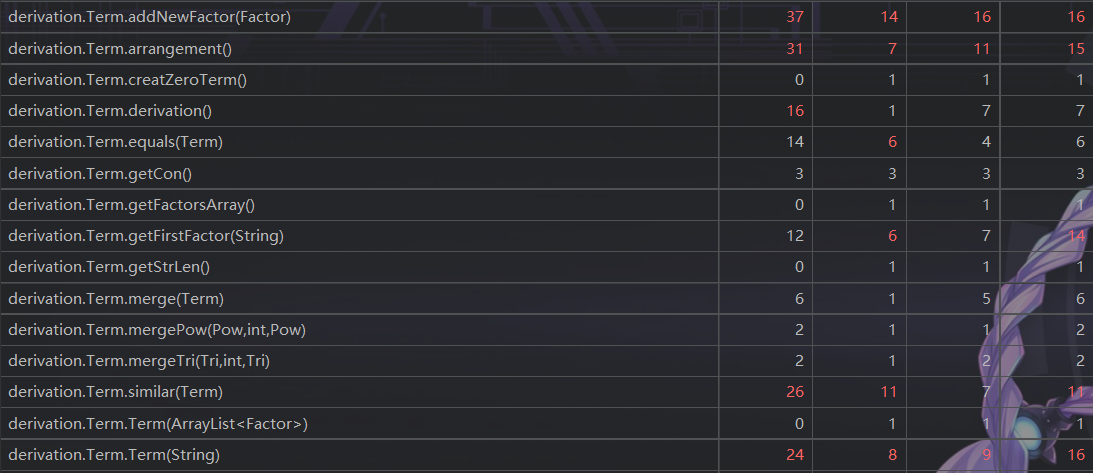

思路分析
解决问题的过程整体上没有较大的变化。
-
输入
为了识别格式问题,取消了预处理步骤。
只在判断
sin和cos关键字后将其替换为了s和c。 -
识别表达式
依旧使用循环遍历的方法,但不再拆分,而是逐一识别。
-
求导
不再选择将括号全部拆开再进行求导,而是增加了对表达式因子的求导。
-
优化
只考虑了合并同类项的优化,即对除常系数因子外全部相同的项进行合并。
-
输出
依旧是逐项循环输出。
设计分析
本次作业选择了重构,使用了十一个类。
-
Derivation、Print
依旧实现了这两个类,功能没有较大变化。
-
Poly、Term
分别实现了多项式和项,包括了构造、合并、求导等基础方法。
根据需要也实现了判断相等的方法。
内部均以
ArrayList为容器组织数据。 -
Factor
抽象类,负责定义不同因子的基本方法。
-
Constant、Pow、Tri、PolyFactor
分别实现了四种不同的因子,同时
Tri内部又以boolean类型变量来区分sin和cos。内部包括了构造、查询方法,也实现了求导和比较。
-
IntegerRewrite
为了识别带符号整数,重写了一个类,包含了整数的识别、查询等方法。
-
Factory
只包含了一个静态方法,用于识别各类元素,识别后转到对应的构造方法。
因为一些原因,我直到周六晚23:00才翻开指导书下次不敢了,对着之前写的代码发呆半小时后,毅然决然地决定从新建文件夹开始重写。。。最后因为时间紧急,外加通宵的DeBuff,写出来的东西很混乱。。。
不过基本的功能都已经实现,而且着重以面向对象的思维进行了尝试,但从统计数据可以看出,仍有部分类和方法复杂度过高,推测是因为还可以将类的功能进一步划分,面向对象还不是很彻底。
BUG分析
不要通宵写代码
一路上的各种笔误就不一一列举了,直接说一个找了好长时间的逻辑混乱的问题吧。
在将因子加入项中时,如果遇到只含有一项的表达式因子,选择将该表达式内的因子一一加入项中,而不是直接将表达式因子加入项中。
case "PolyFactor" :
ArrayList<Term> termsArray = ((PolyFactor)indexFactor).getPoly().getTermsArray();
if (termsArray.size() == 1) {
ArrayList<Factor> factorArrayList = termsArray.get(0).getFactorsArray();
factorsArray.remove(index);
for (Factor item : factorArrayList) {
addNewFactor(item);
}
return true;
} else {
index++;
}
其中index是遍历项的所有因子时的计步变量,处理方法是将其所有因子加入项中的ArrayList内后按索引删除表达式因子。
但在将因子加入项中时,如果遇到常数系数,则遍历已有的因子,再次遇到常数系数时,则生成一个值为二者之积的新常数系数因子加入项中,并将原来的常数系数因子按索引删除。
if (newFactor instanceof Constant) {
for (index = 0; index < size; index++) {
Factor indexFactor = factorsArray.get(index);
if (indexFactor instanceof Constant) {
BigInteger value = ((Constant) indexFactor).getValue().multiply(((Constant) newFactor).getValue());
Constant merge = new Constant(value);
factorsArray.remove(index);
addNewFactor(merge);
return;
}
}
}
这样一来,当加入的表达式因子中只有一项,且项中含有常数因子,而原项中恰好也有常数因子且在表达式因子之前时,就会导致将表达式因子中的常数因子加入项中时会删除原项中的常数因子,从而使得上一级的index所指的位置不再是应该被删除的表达式因子,最终导致结果错误。
这也许就是面向过程的思维模式导致的过于复杂的结构所具有的隐患。
这个故事告诉我们不要再神志不清的时候写代码
更不要在神志不清的时候Debug
二、发现BUG的策略
三周的尝试中我主要采用了两种方法,但并没有让我找到什么十分有效的途径。。。
-
读代码
最初采用的方式,感觉效率较低,而且很容易误判
对耐心是极大的挑战。
-
生成随机数据测试
方便快捷,省时省力
但是要想真正找到BUG还是要手动构造一些有针对性的数据
wtcl
三、重构经历
在距离第三次作业DDL不到24h的时候选择了重构,根本原因还是若要修改原来的代码使其满足新的要求的话,实在是太复杂了!
下一次绝对要提早做决定
还是不要有下一次了
在重构之前的代码(第二次作业)中,只包含了五个类,其中有两个是完全由静态方法组成的没有道理的强行分类,只有简单的多项式->项的二级关系。在编写代码时始终考虑的是正在处理的字符串此时的状态,以及期望得到的下一步状态,仍然陷在面向过程的思维模式中。
重构之后的代码包含了十一个类,相比之前,对每一类因子都建立了单独的类,并都继承自一个抽象类,对带符号整数也建立了专门的类加以处理,使得在处理数据是的逻辑清晰了很多,各方法之间的嵌套与调用变得十分自然。
但还是有部分类与方法略显复杂冗长,依旧没有完全摆脱面向过程编程的思维,有待进一步提高。
四、心得体会
- 要学会分析与拆解,敏锐地察觉到对象之间的层次关系,从原子级的对象垒起整座大厦,这样的代码逻辑清晰,可扩展性也好
- 下次一定好好学习正则表达式,下次一定
不要把作业拖到最后一天再写更不要通宵到神志不清还在写代码- 最后,感谢各路兄弟们的鼎力相助,也祝大家日有所进,学有所成~
2021-03-28



 浙公网安备 33010602011771号
浙公网安备 33010602011771号