dsu on tree

dsu on tree 是一种能够高效处理子树信息的算法。
具体流程：

• 首先遍历一遍树，预处理出每个点的重儿子。

• 第二次遍历时：

  • 先遍历轻儿子，不保留轻儿子子树内的信息。
  • 遍历重儿子，保留子树内信息。
  • 此时数据结构中保留的是节点重儿子内的信息，此时再次将轻儿子的信息加入数据结构中，然后将这个节点的信息加入到数据结构中，此时该节点子树信息被完整保存在数据结构中。
  • 计算答案。
  • 如果需要删除该子树的信息，就删除。

每个轻子树遍历后删除子树信息是为了防止本子树内的信息错误地保留到其他子树中，而重儿子总是最后遍历，故无需删除。

【模板】点分治

dsu on tree 不仅限于能处理子树内信息，也可以处理一些跨子树信息。
对于一条路径，我们考虑在 LCA 处计算贡献。那么一条路径的构成就是：

• 选取一个点 \(u\) 作为 LCA；
• 在 \(u\) 的一个子树中选取一个点 \(x\)；
• 在 \(u\) 的令一个子树中选取一个点 \(y\)。

由于 \(x,y\) 不在 \(u\) 的同一个子树中，所以 \(u\) 必然是 \(x,y\) 的 LCA。
以下讲解统计的方法：
记录每个点到根的距离 \(dis\)，则 \(x,y\) 之间的路径的长度可以表示为 \(dis_x+dis_y-2\cdot dis_u\)，我们要令

\[dis_x+dis_y-2\cdot dis_u=k \]

移项：

\[dis_x=k+2\cdot dis_u-dis_y \]

在 dsu on tree 过程中，我们保留了重儿子的信息，我们可以按照如下流程操作：

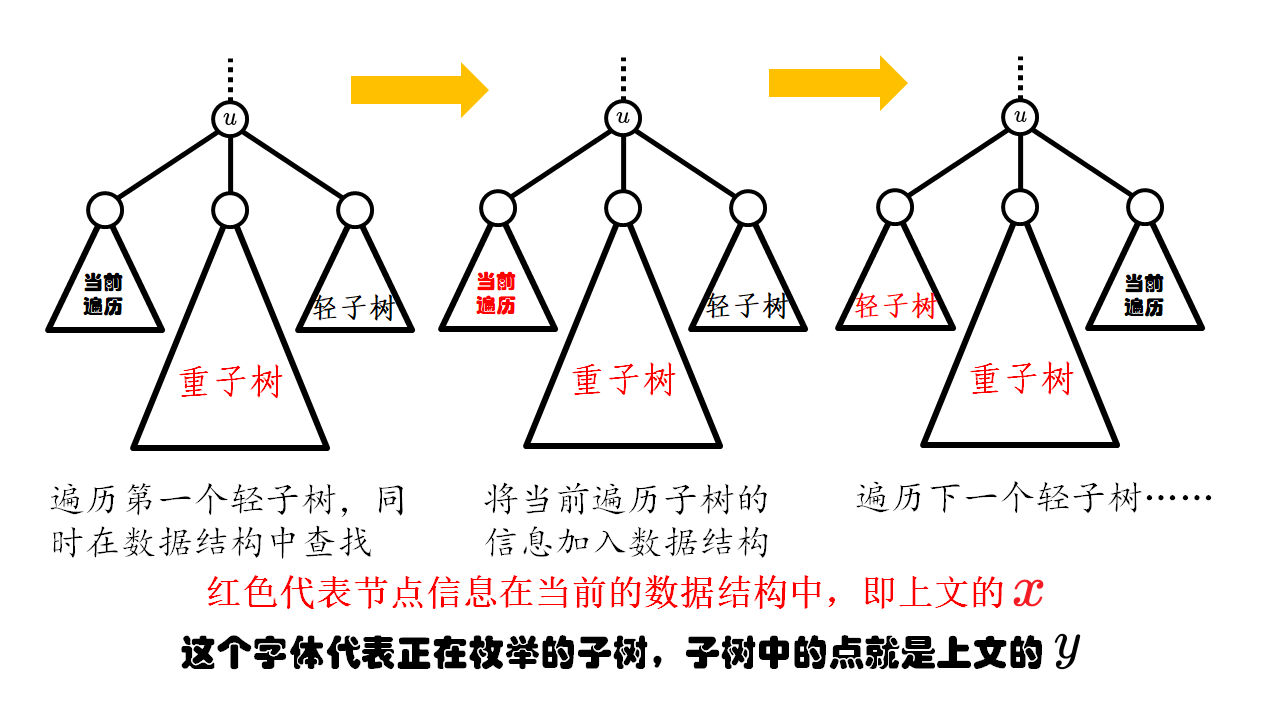
• 首先枚举一个轻子树内的所有点 \(y\)，计算出 \(dis_x=k+2\cdot dis_u-dis_y\)，并在数据结构中查找 \(dis_x\) 是否存在。因为此时数据结构中保留的都是其他子树的信息。
• 计算完毕后将这个轻子树内所有节点的 \(dis_y\) 加入数据结构中，使得其能对以后其他子树的计算产生贡献。

这里的查询只需检查某值是否存在，所以直接用 bool 数组维护信息即可。本题的 \(dis\) 最大达到了 \(10^8\)，可以用 std::bitset 来节省空间。
时间复杂度 \(O(nm\log n)\)。

#include<iostream>
#include<vector>
#include<bitset>
using namespace std;
typedef long long ll;
constexpr int N=1e4+10,V=1e8+10,M=110;
int n,m;
struct edge{int v,w;};
vector<edge> e[N];
int siz[N],son[N],dis[N],k[M];
bool ans[M];
bitset<V> b;
int dfn[N],idfn[N],dfncnt;
void dfs1(int u,int fa){
    dfn[u]=++dfncnt;
    idfn[dfncnt]=u;
    siz[u]=1;
    for(auto [v,w]:e[u]){
        if(v==fa) continue;
        dis[v]=dis[u]+w;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(siz[v]>siz[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int fa,bool keep){
    for(auto [v,w]:e[u]){
        if(v==fa||v==son[u]) continue;
        dfs2(v,u,0);
    }
    if(son[u]) dfs2(son[u],u,1);
    for(auto [v,w]:e[u]){
        if(v==fa||v==son[u]) continue;
        for(int i=1;i<=m;i++){
            if(ans[i]) continue;
            for(int j=dfn[v];j<dfn[v]+siz[v];j++){
                ll d=k[i]+2LL*dis[u]-dis[idfn[j]];
                if(d>=0&&d<=1e8&&b[d]) ans[i]=1;
            }
        }
        for(int i=dfn[v];i<dfn[v]+siz[v];i++)
            b.set(dis[idfn[i]]);
    }
    for(int i=1;i<=m;i++){
        if(ans[i]) continue;
        int d=k[i]+dis[u];
        if(d<=1e8&&b[d]) ans[i]=1;
    }
    b.set(dis[u]);
    if(!keep)
        for(int i=dfn[u];i<dfn[u]+siz[u];i++)
            b.reset(dis[idfn[i]]);
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1,u,v,w;i<n;i++){
        cin>>u>>v>>w;
        e[u].push_back({v,w});
        e[v].push_back({u,w});
    }
    for(int i=1;i<=m;i++) cin>>k[i];
    dfs1(1,0);
    dfs2(1,0,0);
    for(int i=1;i<=m;i++)
        cout<<(ans[i]?"AYE\n":"NAY\n");
    return 0;
}