近期题目合集
abc_405e
简单组合计数。形式化地说,A 必须在 C 左边,A 必须在 D 左边,B 必须在 D左边,不难发现应对 C 进行分割,左半部分与 B 重合,而右半部分与 D 重合。如图
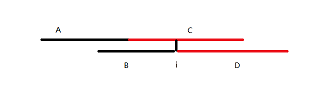
枚举 C 中的断点 \(i\),答案即为
预处理阶乘和逆元可以做到 \(O(n)\)。
【模板】通信题
通信题真好玩。
我们只能使用不大于 \(2^{20}\) 的非负整数存储状态。注意到这个数刚好比 \(10^6\) 略大。这给我们对每一位附上不同权值提供了方便。考虑利用异或运算的性质,给每一位附上当前字符下标的权值(下标从 \(1\))开始,然后求其异或和。将 \(S\) 和 \(T\) 的结果异或起来即得答案。注意下标一定从 \(1\) 开始,否则第一位的值无论如何都是 \(0\)。
communication.cpp
#include<iostream>
using namespace std;
int Alice(string S){
int res=0;
for(int i=0;i<S.length();i++)
res^=(i+1)*(S[i]-'0');
return res;
}
int Bob(string T,int X){
int res=0;
for(int i=0;i<T.length();i++)
res^=(i+1)*(T[i]-'0');
return X^res;
}
『MdOI R1』Group
二分答案。
注意到,对 \(a\) 进行排序,则我们可以选中其中一段连续的区间,计算它的方差。而两侧的值直接设为区间的平均值,不产生贡献。这样是最优策略。在检查合法性时直接从 \(1\) 到 \(n\) 枚举区间就好了,预处理前缀和和前缀平方和可做到 \(O(1)\) 求方差。
二分时,\(l\) 必须从 \(1\) 开始。
code
#include<cstdio>
#include<algorithm>
#include<cmath>
template<typename T>
void read(T &x){
bool f=0;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
if(f)
x=~x+1;
return;
}
template<typename T,typename...Args>
void read(T &x,Args &...args){
read(x);
read(args...);
return;
}
typedef long long ll;
const int N=2e5+10;
int n,a[N],l,r;
ll m,sum[N][2];
bool check(int len){
for(int l=1,r=l+len-1;r<=n;l++,r++){
ll s=sum[r][0]-sum[l-1][0];
double p=1.0*s/len;
double res=len*p*p;
res-=2*s*p;
res+=sum[r][1]-sum[l-1][1];
if(res<=m)
return 1;
}
return 0;
}
int main(){
read(n,m);
for(int i=1;i<=n;i++)
read(a[i]);
std::sort(a+1,a+1+n);
for(int i=1;i<=n;i++){
sum[i][0]=sum[i-1][0]+a[i];
sum[i][1]=sum[i-1][1]+1ll*a[i]*a[i];
}
l=1,r=n;
while(l<=r){
int mid=(l+r)/2;
if(check(mid))
l=mid+1;
else
r=mid-1;
}
printf("%d",n-r);
return 0;
}
[NOIP 2014 提高组] 飞扬的小鸟
\(dp_{i,j}\) 表示在 \((i,j)\) 所用的最少点击屏幕数,显然有朴素转移方程
时间复杂度 \(O(nm^2)\)。
考虑优化,复杂度瓶颈在于 \(k\) 的枚举。我们发现,可以使用类似完全背包的处理,从 \(dp_{i,j-(k-1)\times x_{i-1}}\) 转移到 \(dp_{i,j-k\times x_{i-1}}\) 而不必从 \(dp_{i-1}\) 转移。时间复杂度 \(O(nm)\)。
注意要先处理点击屏幕的情况,否则可能出现同一横坐标既向下又向上的情况。
code
#include<cstdio>
#include<cstring>
template<typename T>
void read(T &x){
bool f=0;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
if(f)
x=~x+1;
return;
}
template<typename T,typename...Args>
void read(T &x,Args &...args){
read(x);
read(args...);
return;
}
template<typename T>
T Min(const T &a,const T &b){
return a<b?a:b;
}
template<typename T,typename...Args>
T Min(const T &a,const T &b,const Args &...args){
return Min(Min(a,b),args...);
}
#define inf 0x3f3f3f3f
const int N=10010,M=1010;
int n,m,k,x[N],y[N],dp[N][M],cnt,res;
struct node{
int l,h;
}c[N];
int main(){
memset(dp,0x3f,sizeof(dp));
read(n,m,k);
for(int i=0;i<n;i++)
read(x[i],y[i]);
for(int i=1,p;i<=k;i++){
read(p);
read(c[p].l,c[p].h);
}
for(int i=1;i<=m;i++)
dp[0][i]=0;
for(int i=1;i<=n;i++){
for(int j=x[i-1]+1;j<=m;j++)
dp[i][j]=Min(dp[i][j],dp[i-1][j-x[i-1]]+1,dp[i][j-x[i-1]]+1);
for(int j=m-x[i-1];j<=m;j++)
dp[i][m]=Min(dp[i][m],dp[i-1][j]+1,dp[i][j]+1);
for(int j=1;j+y[i-1]<=m;j++)
dp[i][j]=Min(dp[i][j],dp[i-1][j+y[i-1]]);
if(c[i].h){
cnt++;
for(int j=1;j<=c[i].l;j++)
dp[i][j]=inf;
for(int j=c[i].h;j<=m;j++)
dp[i][j]=inf;
}
bool f=1;
for(int j=1;j<=m;j++)
if(dp[i][j]!=inf){
f=0;
break;
}
if(f){
printf("0\n%d\n",cnt-1);
return 0;
}
}
res=inf;
for(int i=1;i<=m;i++)
res=Min(res,dp[n][i]);
printf("1\n%d\n",res);
return 0;
}
邦邦的大合唱站队
状压 DP,每一位表示一种乐队。预处理前缀和计算长度。代码实现也很简单。(很久没有独立想出过 DP 题了)
code
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
template<typename T>
T Min(const T &a,const T &b){
return a<b?a:b;
}
const int N=1e5+10;
int n,m,a,dp[1<<21],sum[N][30],len[1<<21];
vector<int> t[30];
#define lowbit(x) x&-x
int main(){
memset(dp,0x3f,sizeof(dp));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a);
sum[i][a-1]++;
for(int j=0;j<m;j++)
sum[i][j]+=sum[i-1][j];
}
for(int i=1,bitcnt;i<(1<<m);i++){
bitcnt=0;
for(int j=0;j<m;j++)
if(i>>j&1){
bitcnt++;
len[i]+=sum[n][j];
}
t[bitcnt].push_back(i);
}
dp[0]=0;
for(int i=1;i<=m;i++)
for(int p:t[i])
for(int j=p;j;j^=lowbit(j)){
int k=lowbit(j);
dp[p]=Min(dp[p],dp[p^k]+len[p]-len[p^k]-(sum[len[p]][__lg(k)]-sum[len[p^k]][__lg(k)]));
}
printf("%d",dp[(1<<m)-1]);
return 0;
}
可持久化并查集
用可持久化数组实现。使用按秩合并但不使用路径压缩。注意修改 \(fa\) 与修改 \(dep\) 都要新建版本。
code
#include<cstdio>
template<typename T>
void read(T &x){
bool f=0;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
if(f)
x=~x+1;
return;
}
template<typename T,typename...Args>
void read(T &x,Args &...args){
read(x);
read(args...);
return;
}
template<typename T>
void Swap(T &a,T &b){
T c=a;
a=b;
b=c;
return;
}
const int N=1e5+10,M=2e5+10;
struct Tree{
int ls,rs,fa,dep;
}tree[N*50];
int nodetot,root[M],n,m;
void build(int &u,int l,int r){
u=++nodetot;
if(l==r){
tree[u].fa=l;
tree[u].dep=1;
return;
}
int mid=(l+r)/2;
build(tree[u].ls,l,mid);
build(tree[u].rs,mid+1,r);
return;
}
void modify_fa(int old,int &u,int l,int r,int x,int k){
u=++nodetot;
tree[u]=tree[old];
if(l==r){
tree[u].fa=k;
return;
}
int mid=(l+r)/2;
if(x<=mid)
modify_fa(tree[old].ls,tree[u].ls,l,mid,x,k);
else
modify_fa(tree[old].rs,tree[u].rs,mid+1,r,x,k);
return;
}
void modify_dep(int old,int &u,int l,int r,int x){
u=++nodetot;
tree[u]=tree[old];
if(l==r){
tree[u].dep++;
return;
}
int mid=(l+r)/2;
if(x<=mid)
modify_dep(tree[old].ls,tree[u].ls,l,mid,x);
else
modify_dep(tree[old].rs,tree[u].rs,mid+1,r,x);
return;
}
int query_fa(int u,int l,int r,int x){
if(l==r)
return tree[u].fa;
int mid=(l+r)/2;
if(x<=mid)
return query_fa(tree[u].ls,l,mid,x);
else
return query_fa(tree[u].rs,mid+1,r,x);
}
int query_dep(int u,int l,int r,int x){
if(l==r)
return tree[u].dep;
int mid=(l+r)/2;
if(x<=mid)
return query_dep(tree[u].ls,l,mid,x);
else
return query_dep(tree[u].rs,mid+1,r,x);
}
int find(int ver,int x){
int fx=query_fa(root[ver],1,n,x);
if(fx==x)
return x;
return find(ver,fx);
}
void merge(int ver,int x,int y){
x=find(ver-1,x);
y=find(ver-1,y);
if(x==y){
root[ver]=root[ver-1];
return;
}
int depx=query_dep(root[ver-1],1,n,x),depy=query_dep(root[ver-1],1,n,y);
if(depx>depy)
Swap(x,y);
modify_fa(root[ver-1],root[ver],1,n,x,y);
if(depx==depy)
modify_dep(root[ver],root[ver],1,n,y);
return;
}
int opt,a,b;
int main(){
read(n,m);
build(root[0],1,n);
for(int i=1;i<=m;i++){
read(opt);
if(opt==1){
read(a,b);
merge(i,a,b);
}
else if(opt==2){
read(a);
root[i]=root[a];
}
else{
read(a,b);
root[i]=root[i-1];
if(find(i,a)==find(i,b))
printf("1\n");
else
printf("0\n");
}
}
return 0;
}
[PA 2024] Modernizacja Bajtocji
挺喜欢这道题,但出在模拟赛里我就不喜欢了。
显然需要维护连通块,连通块内出现环了就说明都有电脑了,连通块是树形的就无法确定。然而这里有一个删除操作。并查集不好进行删除,我们发现被删的点留在连通块内无影响,则考虑对每个人维护 \(id\),删除即为更新 \(id\)。
code
#include<iostream>
using namespace std;
template<typename T>
void Swap(T &a,T &b){
T c=a;
a=b;
b=c;
return;
}
const int N=1.3e6+10;
int fa[N],siz[N];
int find(int x){
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
int n,m,id[N],have[N],cnt;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
fa[i]=i,siz[i]=1,id[i]=i;
cnt=n;
while(m--){
char op;
cin>>op;
int a,b;
if(op=='?'){
cin>>a;
a=id[a];
int p=find(a);
if(siz[p]==1)
cout<<have[p];
else if(have[p])
cout<<1;
else
cout<<'?';
}
else if(op=='+'){
cin>>a>>b;
a=id[a],b=id[b];
int p=find(a),q=find(b);
if(p==q)
have[p]=1;
else{
fa[q]=p;
siz[p]+=siz[q];
have[p]|=have[q];
}
}
else{
cin>>a;
int a1=a;
a=id[a];
int p=find(a);
siz[p]--;
id[a1]=++cnt;
fa[cnt]=cnt;
siz[cnt]++;
}
}
return 0;
}
【模板】最长公共子序列
好早以前欠的一道题,现在补上。
朴素 DP \(O(n^2)\),但这题可以转化为求最长上升子序列。将序列 \(P_1\) 视为是“有序的”,按照 \(P_1\) 的排序规则在 \(P_2\) 中求最长上升子序列,显然这就是答案。实现方面的话开个桶就行。
最长上升子序列 \(O(n\log n)\) 求法:
设 \(dp_i\) 表示到第 \(i\) 个数时的答案,\(t_i\) 表示 \(dp_i\) 对应的序列最大值,显然有 \(dp_i=\max_{j<i \land t_j<b_i} dp_j\),我们可以用树状数组维护前缀 \(\max\),实现 \(O(n\log n)\) 的时间复杂度。
code
#include<cstdio>
template<typename T>
void read(T &x){
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return;
}
template<typename T>
T Max(const T &a,const T &b){
return a<b?b:a;
}
const int N=1e5+10;
int n,a[N],b[N],dp[N],ans;
int tree[N];
#define lowbit(x) x&-x
void modify(int x,int k){
for(;x<=n;x+=lowbit(x))
tree[x]=Max(tree[x],k);
return;
}
int query(int x){
int res=0;
for(;x;x^=lowbit(x))
res=Max(tree[x],res);
return res;
}
int main(){
read(n);
for(int i=1,t;i<=n;i++)
read(t),a[t]=i;
for(int i=1;i<=n;i++){
read(b[i]);
dp[i]=query(a[b[i]])+1;
modify(a[b[i]],dp[i]);
ans=Max(ans,dp[i]);
}
printf("%d\n",ans);
return 0;
}
[CQOI2017] 小Q的棋盘
也是模拟赛的史,可以树形 DP,但我选择贪。
优先走最长链,如果还有剩余步数就需要每两步访问一个新节点。
code
#include<cstdio>
#include<vector>
using namespace std;
template<typename T>
void read(T &x){
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return;
}
template<typename T,typename...Args>
void read(T &x,Args &...args){
read(x);
read(args...);
return;
}
template<typename T>
T Max(const T &x,const T &y){
return x<y?y:x;
}
template<typename T>
T Min(const T &x,const T &y){
return x<y?x:y;
}
const int N=114;
int v,n,maxdep;
vector<int> e[N];
void dfs(int u,int fa,int dep){
maxdep=Max(maxdep,dep);
for(int v:e[u]){
if(v==fa)
continue;
dfs(v,u,dep+1);
}
return;
}
int main(){
read(v,n);
for(int i=1,a,b;i<v;i++){
read(a,b);
a++,b++;
e[a].push_back(b);
e[b].push_back(a);
}
dfs(1,0,1);
if(n<=maxdep-1)
printf("%d\n",n+1);
else
printf("%d\n",Min(v,maxdep+(n-maxdep+1)/2));
return 0;
}
SZA-Cloakroom
很巧妙的一道 DP。显然可以将物品和询问离线下来分别按时间排序。设 \(dp_k\) 表示总价值为 \(k\) 的物品能拿走的最后的时间。转移
表示新加入物品 \(j\),我们能否凑出 \(k\) 决定于最早被取走的那个物品的时间,所以取 \(\min\),而我们显然希望这个值越晚越好,所以取 \(\max\),则只要 \(dp_k>m_i+s_i\) 就说明合法。
初始状态所有 \(dp\) 均为 \(-\inf\),表示均不合法。\(dp_0\) 为 \(\inf\) 表示不选任何物品总是可行的。
code
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1010,M=1e6+10;
struct node{
int c,a,b;
bool operator<(const node &x)const{
return a<x.a;
}
}t[N];
struct query{
int m,k,s,id;
bool operator<(const query &x)const{
return m<x.m;
}
}q[M];
template<typename T>
inline T Max(const T &x,const T &y){
return (x<y?y:x);
}
template<typename T>
inline T Min(const T &x,const T &y){
return (x<y?x:y);
}
int n,p,dp[100010],ans[M];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
cin>>t[i].c>>t[i].a>>t[i].b;
sort(t+1,t+1+n);
cin>>p;
for(int i=1;i<=p;i++)
cin>>q[i].m>>q[i].k>>q[i].s,q[i].id=i;
sort(q+1,q+1+p);
memset(dp,0xcf,sizeof(dp));
dp[0]=2e9;
for(int i=1,j=1;i<=p;i++){
for(;t[j].a<=q[i].m&&j<=n;j++)
for(int k=100000;k>=t[j].c;k--)
dp[k]=Max(dp[k],Min(dp[k-t[j].c],t[j].b));
ans[q[i].id]=dp[q[i].k]>(q[i].m+q[i].s);
}
for(int i=1;i<=p;i++)
printf(ans[i]?"TAK\n":"NIE\n");
return 0;
}
abc_288f
设 \(dp_i\) 表示前 \(i\) 位的答案,有朴素的转移
化简:
可以维护前缀和实现 \(O(n)\)。
code
#include<cstdio>
#define mod 998244353
typedef long long ll;
const int N=2e5+10;
int n,x;
ll sum,dp;
int main(){
scanf("%d %1d",&n,&x);
dp=sum=x;
for(int i=2;i<=n;i++){
scanf("%1d",&x);
dp=(dp*10%mod+sum*x%mod+x)%mod;
sum=(sum+dp)%mod;
}
printf("%lld\n",dp);
return 0;
}
小 a 和 uim 之大逃离
我们事实上只关注二者的差,所以无需分别记录状态。\(dp_{i,j,t,0/1}\) 表示在 \((i,j)\),二者之差为 \(t\),当前应为小 a/uim 走。转移很朴素,看代码吧。
code
#include<cstdio>
#define mod 1000000007
const int N=810;
int n,m,k,a[N][N],dp[N][N][20][2],ans;
int main(){
scanf("%d%d%d",&n,&m,&k);
k++;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
dp[i][j][a[i][j]%k][0]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int t=0;t<=k;t++){
dp[i][j][t][0]=(dp[i][j][t][0]+dp[i-1][j][(t-a[i][j]+k)%k][1])%mod;
dp[i][j][t][0]=(dp[i][j][t][0]+dp[i][j-1][(t-a[i][j]+k)%k][1])%mod;
dp[i][j][t][1]=(dp[i][j][t][1]+dp[i-1][j][(t+a[i][j])%k][0])%mod;
dp[i][j][t][1]=(dp[i][j][t][1]+dp[i][j-1][(t+a[i][j])%k][0])%mod;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans=(ans+dp[i][j][0][1])%mod;
printf("%d\n",ans);
return 0;
}
[SDOI2010] 地精部落
\(dp_{j,0/1}\) 表示前 \(i\) 个数中最后一个是第 \(j\) 大的数的升/降序方案数。
code
#include<iostream>
using namespace std;
const int N=4210;
int n,p,dp[N][2],sum[N][2];
int main(){
cin>>n>>p;
sum[1][0]=sum[1][1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
dp[j][0]=sum[j-1][1]%p;
dp[j][1]=(sum[i-1][0]-sum[j-1][0]+p)%p;
}
for(int j=1;j<=i;j++){
sum[j][0]=(dp[j][0]+sum[j-1][0])%p;
sum[j][1]=(dp[j][1]+sum[j-1][1])%p;
}
}
cout<<(sum[n][0]+sum[n][1])%p<<'\n';
return 0;
}
[SCOI2009] 游戏
神仙题,转化太难想了。观察题目给的实例,发现转化关系可分为 \(3\) 组,不难看出每组的周期应为该组内元素数量,总排数即为各组的元素数的 \(\operatorname{lcm}\) 再加 \(1\)。接下来想如何不重地枚举所有对应关系。考虑使用质因数分解。使用类似完全背包的写法,这样就保证了所有方案的枚举。
code
#include<cstdio>
const int N=1010;
typedef long long ll;
int n,prime[N],e[N],tot;
ll dp[N],res;
int main(){
scanf("%d",&n);
if(n==1){
printf("1\n");
return 0;
}
for(int i=2;i<=n;i++){
if(!e[i])
prime[e[i]=++tot]=i;
for(int j=1;j<=e[i]&&prime[j]*i<=n;j++)
e[prime[j]*i]=j;
}
dp[0]=1;
for(int i=1;i<=tot;i++)
for(int j=n;j>=prime[i];j--)
for(int k=prime[i];k<=j;k*=prime[i])
dp[j]+=dp[j-k];
for(int i=1;i<=n;i++)
res+=dp[i];
printf("%lld\n",res+1);
return 0;
}
[LnOI2019] 真正的 OIer 从不女装
我们发现,女装只有零次和无数次。所以将 \(k>0\) 的情况视为 \(k=1\)。线段树维护区间最长连续段、包含最左/右端最长连续段。
code
#include<cstdio>
#include<algorithm>
using std::max;
using std::min;
template<typename T>
inline void read(T &x){
bool f=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
if(f) x=~x+1;
}
template<typename T,typename...Args>
void read(T &x,Args &...args){read(x);read(args...);}
constexpr int N=2e5+10;
int n,m;
struct Seg{
int maxn,maxl,maxr,tag,vall,valr,len;
Seg(int maxn=0,int maxl=0,int maxr=0,int tag=0,int vall=0,int valr=0,int len=0):
maxn(maxn),maxl(maxl),maxr(maxr),tag(tag),vall(vall),valr(valr),len(len){}
friend Seg operator+(const Seg &a,const Seg &b){
if(!a.len) return b;
if(!b.len) return a;
Seg res;
res.maxn=max(a.maxn,b.maxn);
res.maxl=a.maxl,res.maxr=b.maxr;
res.vall=a.vall,res.valr=b.valr;
res.len=a.len+b.len;
if(a.valr==b.vall){
res.maxn=max(res.maxn,a.maxr+b.maxl);
if(a.maxl==a.len) res.maxl+=b.maxl;
if(b.maxr==b.len) res.maxr+=a.maxr;
}
return res;
}
}tree[N<<2];
#define ls (u<<1)
#define rs (u<<1|1)
void build(int u,int l,int r){
if(l==r){
int val;
read(val);
tree[u]=Seg(1,1,1,0,val,val,1);
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
tree[u]=tree[ls]+tree[rs];
}
inline void push_down(int u){
if(!tree[u].tag) return;
int lenl=tree[ls].len,lenr=tree[rs].len,val=tree[u].tag;
tree[ls]=Seg(lenl,lenl,lenl,val,val,val,lenl);
tree[rs]=Seg(lenr,lenr,lenr,val,val,val,lenr);
tree[u].tag=0;
}
void modify(int u,int l,int r,int x,int y,int k){
if(x<=l&&y>=r){
int len=tree[u].len;
tree[u]=Seg(len,len,len,k,k,k,len);
return;
}
push_down(u);
int mid=(l+r)>>1;
if(x<=mid) modify(ls,l,mid,x,y,k);
if(y>mid) modify(rs,mid+1,r,x,y,k);
tree[u]=tree[ls]+tree[rs];
}
Seg query(int u,int l,int r,int x,int y){
if(x<=l&&y>=r) return tree[u];
Seg res;
push_down(u);
int mid=(l+r)>>1;
if(x<=mid) res=res+query(ls,l,mid,x,y);
if(y>mid) res=res+query(rs,mid+1,r,x,y);
return res;
}
int x,y,k;
int main(){
read(n,m);
build(1,1,n);
while(m--){
char ch=getchar();
while(ch!='R'&&ch!='Q') ch=getchar();
read(x,y,k);
if(ch^'Q') modify(1,1,n,x,y,k);
else if(k==0)
printf("%d\n",query(1,1,n,x,y).maxn);
else{
Seg temp=query(1,1,n,x,y);
int res=temp.maxn;
if(temp.vall==temp.valr) res=max(res,temp.maxl+temp.maxr);
printf("%d\n",min(res,temp.len));
}
}
return 0;
}
[NOIP 2004 提高组] 合并果子 加强版
传统做法中堆的 \(O(n\log n)\) 复杂度太高了,我们使用两个队列,先桶排,然后按顺序插入队列 \(q_1\) 中,之后每合并一次就将结果插入队列 \(q_2\) 中,容易发现,\(q_1\) 和 \(q_2\) 都具有单调性,所以每次只需从两个队列的队头取出 \(2\) 个最小的数即可。时间复杂度 \(O(n)\)。注意读入的常数。
使用这种思路,做 [NOIP 2016 提高组] 蚯蚓。
code
#include<cstdio>
#include<queue>
using namespace std;
#ifdef __linux__
#define getchar getchar_unlocked
#endif
template<typename T>
void read(T &x){
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return;
}
typedef long long ll;
const int M=1e5+10;
int n,a,b[M];
queue<ll> q1,q2;
ll sum;
ll get_min(){
if(q1.empty()){
ll x=q2.front();
q2.pop();
return x;
}
if(q2.empty()){
ll x=q1.front();
q1.pop();
return x;
}
if(q1.front()<q2.front()){
ll x=q1.front();
q1.pop();
return x;
}
ll x=q2.front();
q2.pop();
return x;
}
int main(){
read(n);
for(int i=1;i<=n;i++)
read(a),b[a]++;
for(int i=1;i<=1e5;i++)
while(b[i]--)
q1.push(i);
for(int i=1;i<n;i++){
ll x=get_min(),y=get_min();
q2.push(x+y);
sum+=x+y;
}
printf("%lld\n",sum);
return 0;
}
多人背包
也是很久以前的题,之前好几次想写都觉得太抽象写不了,今天静下心来想一想其实并不难。
\(dp_{j,k}\) 表示容量为 \(j\) 时的第 \(k\) 优解。我们直接双指针枚举选或不选当前物品,枚举出当前的前 \(k\) 优,将它们存入队列中然后直接转移。时间复杂度 \(O(nvk)\),空间复杂度 \(O(vk)\)。
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
int k,v,n,a[210],b[210],dp[5010][60],temp[60];
ll ans;
int main(){
memset(dp,0xcf,sizeof(dp));
cin>>k>>v>>n;
for(int i=1;i<=n;i++)
cin>>a[i]>>b[i];
dp[0][1]=0;
for(int i=1;i<=n;i++)
for(int j=v;j>=a[i];j--){
int p1=1,p2=1,cnt=0;
while(cnt<=k){
if(dp[j][p1]>dp[j-a[i]][p2]+b[i])
temp[++cnt]=dp[j][p1++];
else
temp[++cnt]=dp[j-a[i]][p2++]+b[i];
}
for(int t=1;t<=k;t++)
dp[j][t]=temp[t];
}
for(int i=1;i<=k;i++)
ans+=dp[v][i];
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号