算法学习(17):哈希函数和哈希表的实现
哈希函数和哈希表的实现
哈希函数的特点
- 输入域无穷:例如可以输入任意长度的字符;输出域有限:如16位16进制的数
- same in -> same out 无随机性
- 哈希碰撞
- 相似输入也会导致输出比较离散;达到一定数量时这些输出在输出域上是较为均匀分布的
由第四条可以推出,所有输出mod m后,这些输出在0~m-1上也是均匀分布的,这是一个比较重要的推论
某个大文件存有40亿个无符号整数(0~232-1范围,大概是43亿),如果只提供1G内存,怎么返回出现次数最多的数
经典解法(不可行)
遍历这40亿个整数,加进哈希表里,key值存放遍历到的整数,value存这个整数出现的次数,每出现一次value+1,如果不考虑索引空间的浪费,这样每条记录两个int占空间8字节,最坏的情况是40亿数字各不相同,则共占8*40亿≈32G,空间就不够用。
第二种方法(正确解)
哈希表内存的使用与整数的种类相关,利用上面第四条性质的推论,将每个数字计算出的哈希值mod 100,这样不同种类的数字就会较为均匀地分布在0~99范围内,在外存里准备100个小文件,把不同种类的数字存进对应的小文件中,相同的数由于计算到的哈希值一样,mod之后的值也一样,所以会进相同的小文件。在使用的时候每次只调用一个小文件,然后进行上面的经典解法的步骤统计当前小文件中出现次数最多的数字,这样内存就是(32/100) G,不到1G,统计完当前文件释放掉内存,继续去统计下一个小文件里的数字,统计完100个小文件就能得出出现次数最多的数字
经典哈希表的设计原理
结构原理:先准备长度为m的空间,将需要储存的内容调用哈希函数计算出一个哈希值,然后将这个哈希值mod m,得出的结果r就会在0~m-1范围内,将要储存的内容就存储在长度为k的空间的第r个位置,存储的方式是单链表形式,下一次另外的内容又计算出r,就通过单链表连在上次存在r位置的内容的后面。由于mod m之后的值是均匀分布的,所以每个位置链表的长度也都大概相同。在查找的时候,怎么存的就怎么找,找到在m中的位置后遍历单链表找。但是大量加入储存内容,单链表的长度就会越来越长,这时候就需要扩容。设置一个变量k统计单链表的长度,一旦有一条单链表超过这个长度(由于其他链表的长度都差不多,所以它们也都逼近k),则触发扩容逻辑。假设扩容成2m,原来储存在m长度空间里的内容都重新计算哈希值,然后mod 2m,存在新空间里。如果有N条数据,扩容操作的时间复杂度是O(logN),移动数据的时间复杂度是O(N),整体的时间复杂度是O(NlogN),加了N个数据代价是O(NlogN),单个数据的代价是O(logN)。
既然单个数据的代价是O(logN),那为什么还说哈希表的增删改查是O(1)呢,原因有以下两点:
- 当把单链表长度阈值K定的较大,可以极大的降低扩容代价,把时间复杂度从O(logN)降低成常数级别
- java和jvm等一些虚拟机语言可以利用离线扩容技术不占用用户在线时间,进一步降低哈希表使用代价
所以说哈希表在使用的时候可以认为是O(1),而不是理论上。
在具体各个语言在实现哈希表的方法中,还有不同的改进方法进一步降低使用代价,比如开放地址法等
设计RandomPool结构
设计一种结构,在该结构中有如下三个功能:
- insert(key):将某个key加入到该结构,做到不重复加入
- delete(key):将原本在结构中的某个key移除
- getRandom():等概率随即返回结构中的任何一个key
要求三种方法的时间复杂度都是O(1)
准备一个int型变量,储存size,准备两个哈希表,第一个key是储存的数据,value是索引(0~size-1),另一个哈希表刚好相反。
- insert(key)方法就是第一张表插入要储存的数据,value是size+1,另一张表相反,最后size++。
- getRandom()方法是利用系统提供的随机函数,产生一个0~size-1之间的随机数,返回以这个随机数为索引的数据。
- delete(key)先查询key值是否存在,如果不存在就不做操作;如果存在,则把最后加入的一条索引为size-1的数据的索引改为要删除那条数据的索引,另一张表则是把要删除的数据的索引对应的value改为索引为size-1的数据,size--。这样可以保证索引是连续的,中间不会产生间隔,导致无法取0~size-1之间随机数返回随机值。
C++代码实现:
class RandomPool
{
public:
RandomPool()
{
m_Size = 0;
}
void insert(string str)
{
m_StringMap.insert(make_pair(str, m_Size));
m_IndexMap.insert(make_pair(m_Size, str));
m_Size++;
}
void Delete(string str)
{
if (m_StringMap.count(str) == 0)
{
return;
}
int index = m_StringMap.at(str);
string temp = m_IndexMap.at(m_Size - 1);
m_StringMap.at(temp) = index;
m_IndexMap.at(m_Size - 1) = str;
m_StringMap.erase(str);
m_IndexMap.erase(index);
}
string getRandom()
{
srand((unsigned)time(NULL));
int randomIndex = rand() % m_Size;
return m_IndexMap.at(randomIndex);
}
private:
unordered_map<string, int> m_StringMap;
unordered_map<int, string> m_IndexMap;
int m_Size;
};
布隆过滤器
位图
什么是位图
位图BitMap,每一位是一个bit,由0和1组成,各代表一个状态。位图可以用int数组来表示,假设数组的长度是n,一个int类型是4字节,32bit,这样就可以代表32*n位的位图,可以极大的节省内存空间
C++实现位图的各种操作
int arr[10] = { 0 }; //32bit * 10 -> 320 bits 的位图
//arr[0] 可以代表 0~31位的信息
//arr[1] 可以代表 32~63位的信息
//arr[0] 可以代表 64~95位的信息
//…………
int i = 178; //准备拿到第178位的信息
int numIndex = i / 32; //找到第178位在数组中数字的下标
int bitIndex = i % 32; //找到第178位在数组中数字所代表的32里的第几位
//拿到第178位的信息
int status = (arr[numIndex] >> bitIndex) & 1;
//把第178位的状态改成1
arr[numIndex] = arr[numIndex] | (1 << bitIndex);
//把第178位的状态改成0
arr[numIndex] = arr[numIndex] & (~(1 << bitIndex));
什么是布隆过滤器
布隆过滤器(Bloom Filter)是由 Bloom 于 1970 年提出的。我们可以把它看作由二进制向量(或者说位数组)和一系列随机映射函数(哈希函数)两部分组成的数据结构。
布隆过滤器的原理
取一个长度为 m bit的数组,初始值都是0,它在计算机里占用m/8大小的字节,将需要添加的数据用k个不相关的哈希函数计算出k个哈希值,然后每一个哈希值都 mod m,得出在数组中的位置,把这k个位置的状态都改为1。查找一条数据是否被过的时候,把这条数据也用之前的k个哈希函数计算k个哈希值,mod m找到k个位置,然后看这k个位置状态是否都为1,如果全都是1,那么就添加过这条数据,如果有一个位置不是1,那么就没有添加过这条数据。在添加数据的过程中如果数据量过大,m不够大,肯定会有不同的数据计算出一样的位置,这就会产生误差,没有被添加过的数据可能会被误报为添加过。
布隆过滤器的优缺点
优点:
- 相比于我们平时常用的的 List、Map 、Set 等数据结构,它占用空间更少并且效率更高,
缺点:
- 其返回的结果是有误差,没有被添加过的数据可能会被误报为添加过(添加过而被误报为没有添加过的误差情况是不会出现的,这是由布隆过滤器的原理决定的)。理论情况下添加到集合中的元素越多,误报的可能性就越大。但是这种误差的概率可以由优化过后的设计而降低。
- 存放在布隆过滤器的数据不容易删除。
布隆过滤器失误率分析
P代表失误率,m代表数组长度,k代表哈希函数个数
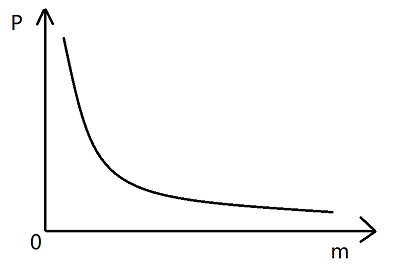
如上图,k不变,随着m的增大,P是越来越小的,但是边际效益是递减的
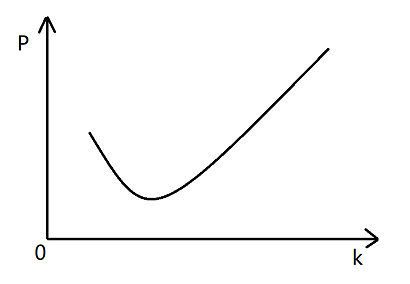
如上图,m不变,随着k的增大,一开始p是越来越小的,但是k一旦超过一定量,p又会越来越大
适用场景
- 判断给定数据是否存在:比如判断一个数字是否存在于包含大量数字的数字集中(数字集非常大)、 防止缓存穿透(判断请求的数据是否有效避免直接绕过缓存请求数据库)等等、邮箱的垃圾邮件过滤、黑名单功能等等。
- 去重:比如爬给定网址的时候对已经爬取过的 URL 去重。
模型适用条件
- 涉及不删除操作
- 允许一定概率的误差
最佳的m与k的计算公式以及实际失误率的计算公式
首先需要两个值,样本数量n(与单个样本的大小无关)和允许的失误率P
- m = -((n*lnP)/(ln2)2) 向上取整
- k = ln2*(m/n) 向上取整
- P真 = 1 - e-(n*k真)/m真
当m与k真求出来并向上取整后,如果有比求出来的m更大的内存空间可以提供,则m还可以更大,取m真,可以利用第三个公式求出真实的失误率,比预计允许的失误率还要低。
一致性哈希问题
当服务器需要储存数据时,如果用的是分布式服务器,会涉及到数据怎么维持的问题,底层服务器怎么组织的问题。
经典的组织方式
假设有三台服务器,当得到一条需要储存的数据时,将它的key利用哈希函数计算出哈希值,然后 mod 3,算出是几就存到哪一台服务器上。利用key查询的时候也是计算出哈希值然后 mod 3找出存放在哪台机器上。这种方式可以做到数据种类在三台数据服务器上均匀分布。高频率查询的key、中频查询的key、低频查询的key种类上在三台服务器上都是均分的,所以也做到了负载均衡。一定要选择种类多的key做数据划分的依据,比如:人名、身份证号,不要用国家、性别等种类少的,像性别这种只有两个的甚至会让一台服务器完全不用,这样负载就不均衡了。
虽然这种方式可以做到数据种类在服务器上均匀分布,且负载均衡,但是在增加或减少服务器数量的时候,所有服务器上的所有数据都要重新计算哈希值再mod上新的服务器数量来转移数据,这样数据迁移的代价太大了
一致性哈希
如下图,假设一种哈希算法的输出域是0~232-1,他们收尾相接形成一个环,现在有四台服务器node1到node4,用这四台服务器各自的可以区分开来的数据段来计算哈希值,计算出来的四条哈希值就落在环的四个点上。需要储存的数据根据它的key计算出一个哈希值,顺时针旋转找到距离这个哈希值最近的服务器,把这条数据储存到这台服务器上,这样就可以找到每一条数据的归属。
假设现在需要增加一台服务器,它计算出的哈希值就在node1和node2之间,那么在数据迁移的时候就只需要把原来由node2负责的node1到新加的node5这一段的数据迁移到node5上即可,同样的如果想减少一台服务器,例如node5,只需要把node1到node5这一段的数据迁移到node2上即可,这样数据迁移的代价就会肉眼可见得小得多。
但是这样同时又引出了两个问题
- 服务器台数太少,不能保证均匀地分布在这个环上
- 一旦增加或减少服务器的数量,立刻会有服务器的负载变低或变高,导致负载不均衡
这时虚拟节点技术就可以同时解决上面的两个问题。
假设每台服务器分配1000个虚拟节点
- 不是由4台服务器自己去抢位置了,而是由这4000个节点去抢,这样节点数够多,就能保证均匀地分布在环上
- 节点都可以找到自己所属的服务器,服务器也可以找到具体的某个节点,所以不同服务器的节点之间数据的转移是很容易实现的。当增加服务器时,这台增加的服务器也有自己的若干个节点均匀地分布在环上,这样可以保证均匀地从每台服务器上夺取数量相近的数据;而减少服务器时,这台服务器的节点又能把自己的数据均匀地迁移到每台服务器的节点上。这样就做到了负载均衡
同时一致性哈希搭配虚拟节点技术还能做到管理负载,假设node1这台服务器的性能比其他服务器都强,可以给它分配2000个节点,而node4这台服务器性能较差,就可以只分配500个节点。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号