Word2Vec的前世今生

自然语言处理-词向量模型-Word2Vec

致谢：

https://blog.csdn.net/MR_kdcon/article/details/123171180

https://www.bilibili.com/video/BV1A7411u7zh/

自然语言处理，一个比较基础的工作是词的表示方法，目前用的最多的就是Word Embedding,也就是Word2Vec技术生成的词的表示方式，如果想了解Word2Vec，不得不先提一提简单的One-hot（独热）编码、基于窗口的共现矩阵和分布式（稠密）表示方法（Distributed Representation）。

One-hot编码

拿”hello world“为例，如下图所示。

简单解释独热：只有一位是1，其余是0，热力图表示，就是那一位是独热的。

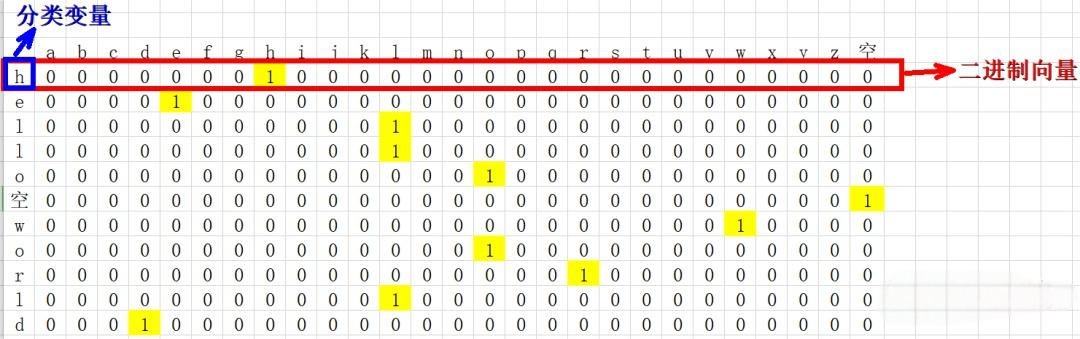
所以，One-hot编码是对于一个包含 n 个不同类别的分类变量，one-hot 编码会创建 n 个二进制特征（或称为“哑变量”），其中每个特征对应一个类别。对于每个样本，如果它属于第 i 个类别，则第 i 个二进制特征的值为 1，其余 n−1 个特征的值为 0。

以上把字母或者单词映射为一串数或者一串向量的过程其实是文本向量化的过程，所以Word2Vec技术也是进行文本向量化的工具，既然One-hot比较简单，但是为什么还会诞生Word2Vec，其实我们从上面图片可以观察到，随着字母或者词的数量的增多，向量化的特征维度也会越来越高，每个向量多余的0会越来越多，并且向量化的目的之一是求余弦相似度，也就是需要就两个向量的点积形式，如果采用One-hot编码，会造成任何两个向量的余弦相似度都是0，也就是任何两个词相似性都为0， 这显然是不合理的，必须要保证相近的词的向量的相似度相对高，这些都造成了One-hot编码的不适用，但是确实简单清楚，总结一下One-hot的缺点就是：

  1. 维度灾难
  2. 稀疏性大
  3. 语义鸿沟

SVD（基于窗口的共现矩阵）

基于窗口的共现矩阵，共现共现，就是共同出现，窗口就是和相邻几个词进行计算。

例如：

  1. I enjoy flying.
  2. I like NLP.
  3. I like deep learning.

如下就是基于窗口的共现矩阵（Window based Co-occurrence Matrix），窗口为2, 首先共现矩阵肯定是对称的，并且维度是\(|C| \times |C|\)，\(|C|\) 是语料库的所有词的数量。

I和like由第2句和第3句话可得，共同出现两次；

like和NLP由第2句可知，共同出现一次；

I和NLP，没有出现过为0；

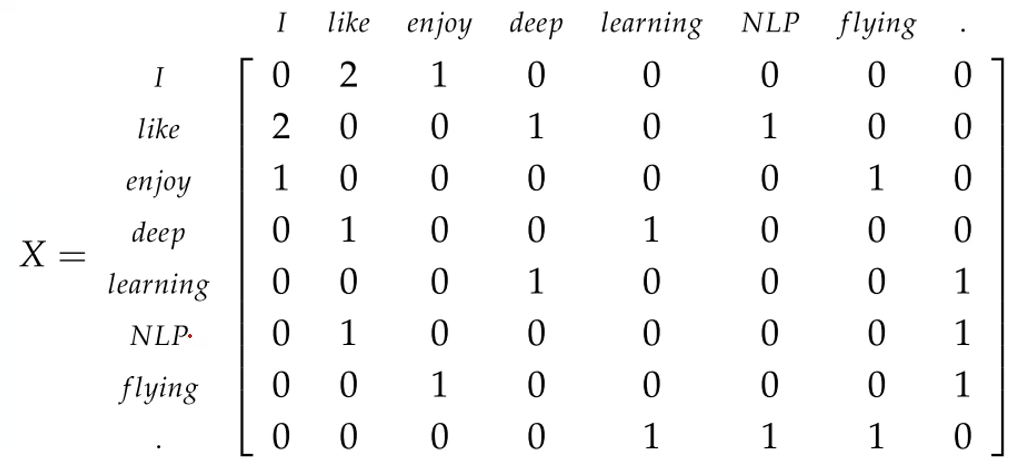
通过观察共现矩阵的大小，还是存在维度灾难，这时候可以利用SVD矩阵分解， SVD将一个矩阵分为\(U,\Delta, V\)，矩阵形式如下：

\[X=U\Delta V^T \]

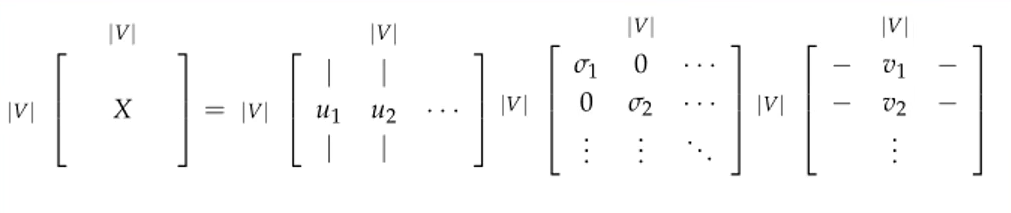
分解为三个矩阵都是\(|V|\times |V|\)大小的，\(\Delta\)​是一个主对角线是奇异值的对角矩阵，奇异值的大小决定向量的重要性，主要思想为： 低秩近似（用少量大奇异值近似原矩阵）。

  • 大奇异值 对应的方向是数据分布的主要方向（主成分），包含更多信息。
  • 小奇异值 对应的方向是次要方向或噪声方向，对整体结构影响微弱。

所以SVD保留前K个奇异值，近似矩阵为:

\[A_k = \sum\limits_{i=1}^k \sigma_iu_iv_i^T \]

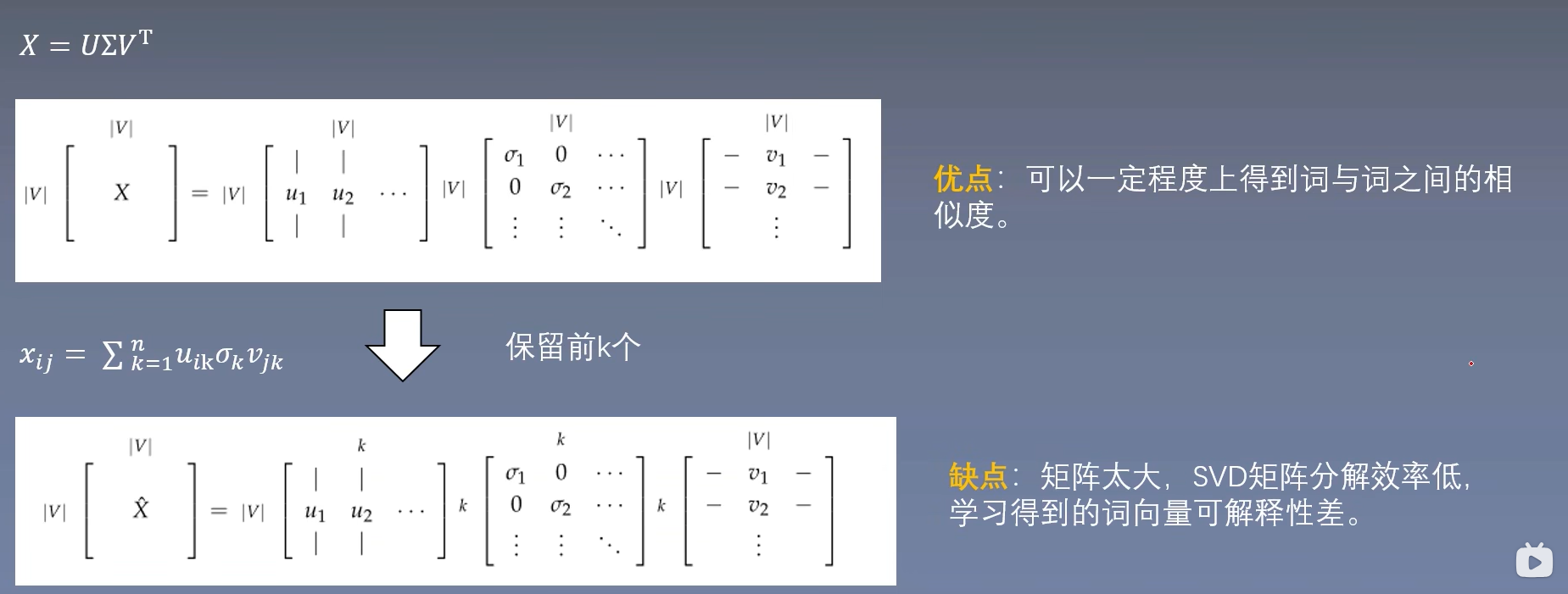
通过这种方式获得的词向量的表示，会从一定程度上得到词与词之间的相似度，但是矩阵过大的话，分解效率低。

[!info]- 奇异值分解（SVD）及其性质证明

（一）前置知识：

  1. 矩阵的特征值和特征向量

\(Ax =\lambda x\), 其中\(A\)是\(n\times n\)大小，\(x\)是一个n维向量。\(\lambda\)是矩阵\(A\)的一个特征值，而\(x\)是矩阵\(A\)的特征值\(\lambda\) 所对应的特征向量。

进一步理解，矩阵\(A\)的信息可以由其特征值和特征向量表示。

则矩阵\(A\)的分解式子为：\(A=W\Sigma W^{-1}\)。

这里引入正交矩阵和标准正交基，正交矩阵是转置等于其逆矩阵的矩阵，即\(A^T=A^{-1}\)。标准正交基，就是一个向量的内积为1，简单来说就是向量每个值的平方求和，表达为符号为\(|| w_i||_2 = 1\)。

因此矩阵分解公式变为\(A=W\Sigma W^T\)。

根据以上方阵的特征值和特征向量的分解，我们可以得到这个矩阵必须是方阵，大小必须是\(n \times n\)的，不适用于普通矩阵，所以SVD分解就被提出来，针对任何矩阵进行分解，那就开始介绍奇异值分解， 首先定义为：

（二）SVD定理定义：

对任意实数矩阵 \(A \in \mathbb{R}^{m \times n}\)，存在正交矩阵 \(U \in \mathbb{R}^{m \times m}\) 和 \(V \in \mathbb{R}^{n \times n}\)，以及对角矩阵 \(\Sigma \in \mathbb{R}^{m \times n}\)，使得：

\[A = U \Sigma V^T, \]

其中：

  • \(\Sigma\) 的对角元素为 奇异值 \(\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_r > 0\)（按降序排列），其余元素为 0。
  • \(r = \text{rank}(A) \leq \min(m, n)\)。
  • \(U^TU=I, V^TV=I\)

(三) 具体证明：

步骤1：构造奇异向量矩阵 \(U\)和\(V\)

既然特征值矩阵分解适用于方阵，那么可以把矩阵\(A\)变成方阵，即\(A^TA\)和\(AA^T\)为方阵，根据特征值和特征向量定义：

\[\begin{aligned} (A^TA)v_i = \lambda_iv_i \\ (AA^T)u_i = \lambda_iu_i \end{aligned} \]

将所有特征向量张成一个\(n \times n\)的矩阵\(U=[u_1 \quad \dots \quad u_n]，V=[v_1 \quad \dots \quad v_n]\),所有特征值张成一个对角矩阵\(\Lambda_1 = \text{diag}(\lambda_1, \dots, \lambda_n)， \Lambda_2 = \text{diag}(\lambda_1, \dots, \lambda_n)\)，且 \(\lambda_i \geq 0\), 则有：

\[\begin{aligned} A^T A = V \Lambda_1 V^T \\ A A^T = U\Lambda_2 U^T \\ \end{aligned} \]

这里的\(,U,V\)就是公式右侧中的\(U,V\), 一般而言，将\(U, V\)的每个特征向量叫做\(A\)的左（右）奇异向量。

步骤2：构造奇异值矩阵\(\Sigma\)

根据已知的\(U\)和\(V\)进行反推，如下公式：

\[A = U \Sigma V^T \implies AV = U \Sigma V^T V \implies AV = U \Sigma \implies Av_i = \sigma_i u_i \implies \sigma_i = \frac{Av_i}{u_i} \]

\[\Sigma = \begin{bmatrix} \Sigma_r & 0 \\ 0 & 0 \end{bmatrix}, \quad \Sigma_r = \text{diag}(\sigma_1, \dots, \sigma_r). \]

（4）关键性质及证明：奇异值的平方是 \(A^T A\) 或 \(A A^T\) 的特征值

性质陈述

若 \(A = U \Sigma V^T\) 是SVD分解，则：

  • \(\sigma_i^2\) 是 \(A^T A\) 和 \(A A^T\) 的特征值。
证明步骤
  1. 计算 \(A^T A\)：

\[ A^T A = V \Sigma^T U^T U \Sigma V^T = V \Sigma^T \Sigma V^T = V \Sigma^2 V^T. \]

  • 其中 \(\Sigma^2 = \text{diag}(\sigma_1^2, \dots, \sigma_r^2, 0, \dots, 0)\)。
  1. 分析特征分解：
  • \(A^T A = V \Sigma^2 V^T\) 表明其非零特征值为 \(\sigma_i^2\)，对应特征向量为 \(V\) 的列向量。
  1. 同理计算 \(A A^T\)：

\[A A^T = U \Sigma V^T V \Sigma^T U^T = U \Sigma \Sigma^T U^T = U \Sigma^2 U^T. \]

  • 非零特征值同样为 \(\sigma_i^2\)，对应特征向量为 \(U\) 的列向量。
结论
  • 奇异值的平方 \(\sigma_i^2\) 是 \(A^T A\) 和 \(A A^T\) 的非零特征值。
  • \(A^T A\) 和 \(A A^T\) 的非零特征值完全一致。

Distributed Representation 词嵌入

为了解决计算复杂，维度灾难，语义鸿沟问题，Distributed Representation应运而生，此时的词向量维度\(D << |V|\),远远小于词的个数，映射的这个向量还有个更好听更高级的英文名字就是Word Embedding,也就是词嵌入。

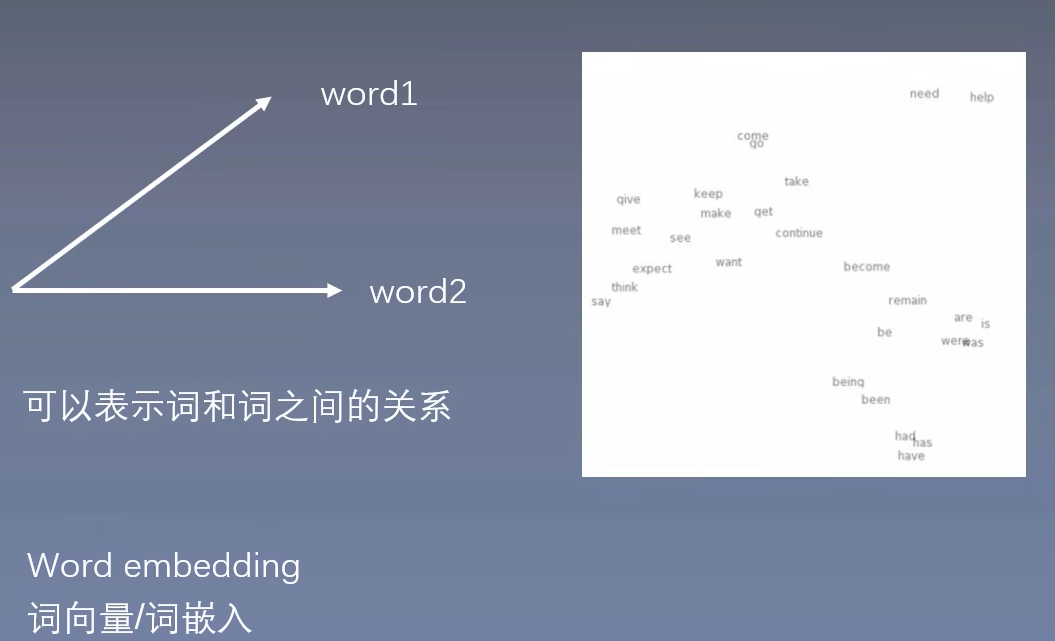
具体来说，就是通过将单词映射到连续的低维向量空间，这不仅解决了维度灾难和稀疏性大的问题，同时也能避免语义鸿沟问题（向量的每一个值0的概率变小，可以是任何实数），也就是说Word2Vec可以保证相近词的向量的相似度（或点积）较高，而不相近的词向量的相似度较低。如下图就是Word2Vec的目的，把相近词映射为相差不多的向量，不相近词反之。



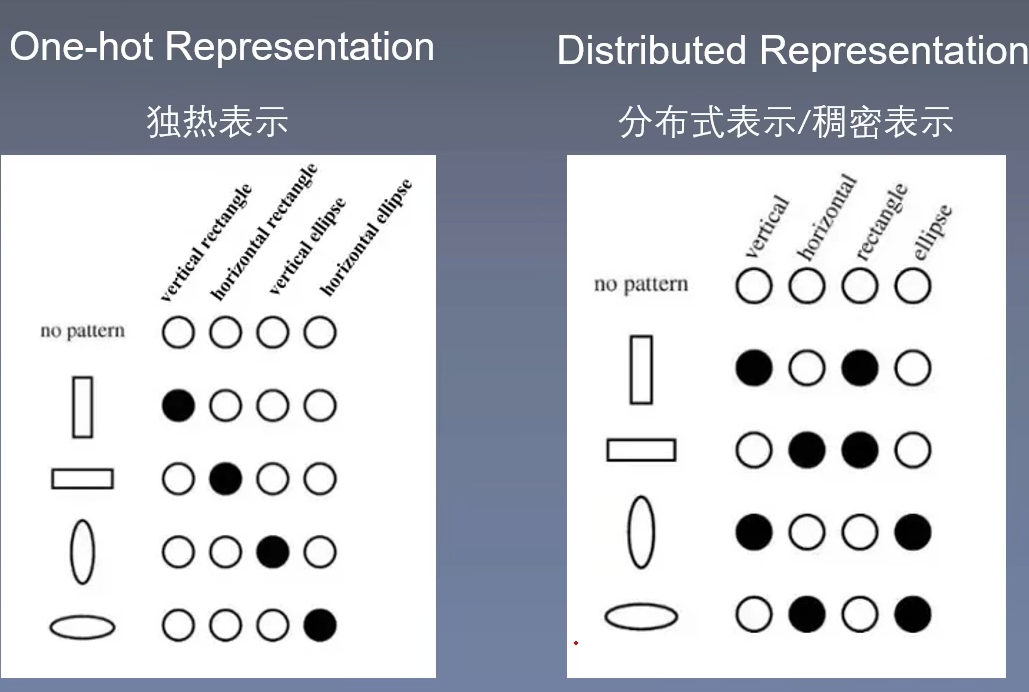
下一步让我们看看Distributed Representation的发展历程， Hinton提出概念，2003年首次使用， 2013年Word2Vec提出，训练快。

那Word2Vec是如何训练得到降低了维度和使得语义相似的单词在向量空间中距离相近的Word Embedding呢?下面正式进入Word2Vec的原理部分。

前置知识

语言模型

  1. 概念

概念：语言模型是计算那一个句子是句子的概率的模型

探究句子是否符合语义和语法

  1. 语言模型的构建
  • 基于专家语法规则的语言的模型：找到统一范式很难
  • 统计语言模型：通过概率计算来刻画语言模型 \(P(s) = P(w_1, w_2, \cdots,w_n) = p(w_1)p(w_2 | w_1) p(w_3 | w_1,w_2) \cdots p(w_n |w_1,w_2, \cdots, w_{n - 1})\)
  1. 统计语言模型

\(sentence = \{w_1, w_2, \cdots, w_n\}\)

用语料的频率代替概率（频率学派）

  • 词 \(w_i\) 的概率：

    \[p(w_i) = \frac{\text{count}(w_i)}{N} \]

  • 词对 \((w_{i-1}, w_i)\) 的概率：

    \[p(w_{i-1}, w_i) = \frac{\text{count}(w_{i-1}, w_i)}{N} \]

条件概率

  • 已知词 \(w_{i-1}\)，求之后出现词 \(w_i\) 的概率：

\[ p(w_i | w_{i-1}) = \frac{p(w_{i-1}, w_i)}{p(w_{i-1})} \]

  • 用频率表示条件概率：

\[p(w_i | w_{i-1}) = \frac{\text{count}(w_{i-1}, w_i)}{\text{count}(w_{i-1})} \]

条件概率公式

  • 一般条件概率公式：

\[P(A | B) = \frac{P(A \cap B)}{P(B)} \]

具体示例

  1. 句子 "张三 很 帅"

\[ P(\text{张三 很 帅}) = P(\text{张三}) \times P(\text{很} | \text{张三}) \times P(\text{帅} | \text{张三}, \text{很}) \]

  1. 句子 "张很帅 很 帅"

\[P(\text{张很帅 很 帅}) = P(\text{张很帅}) \times P(\text{很} | \text{张很帅}) \times P(\text{帅} | \text{张很帅}, \text{很})， \]

P(张很帅)为0，整个概率为0，不合理，原因：有一些词没有出现在语料库当中。

  1. 句子 "张三 很 漂亮"

\[P(\text{张三 很 漂亮}) = P(\text{张三}) \times P(\text{很} | \text{张三}) \times P(\text{漂亮} | \text{张三}, \text{很}) \]

短语太长，也会造成概率为0。

平滑操作

平滑操作与Laplace Smoothing

词或词组存在性

  • 有些词或词组在语料中没有出现过，但这不能代表它不可能存在。

平滑操作

  • 平滑操作就是给那些没有出现过的词或词组也给一个比较小的概率。

Laplace Smoothing（加1平滑）

  • Laplace Smoothing也称为加1平滑：每个词在原来出现次数的基础上加1。

  • 原始计数与概率

    • A: 0, \(P(A) = 0/1000 = 0\)
    • B: 990, \(P(B) = 990/1000 = 0.99\)
    • C: 10, \(P(C) = 10/1000 = 0.01\)

  • 加1平滑后计数与概率

    • A: 1, \(P(A) = 1/1003 = 0.001\)
    • B: 991, \(P(B) = 991/1003 = 0.988\)
    • C: 11, \(P(C) = 11/1003 = 0.011\)

马尔科夫假设

根据\(P(s) = P(w_1, w_2, \cdots,w_n) = p(w_1)p(w_2 | w_1) p(w_3 | w_1,w_2) \cdots p(w_n |w_1,w_2, \cdots, w_{n - 1})\)， 统计语言模型存在参数空间过大和数据稀疏严重的问题，为了解决这个问题，马尔科夫链应运而生。

下一个词的出现仅依赖于前面的一个词或几个词

\[ P(s) = P(w_1, w_2, \dots, w_n) = P(w_1)P(w_2 | w_1)P(w_3 | w_1 w_2) \dots P(w_n | w_1 w_2 \dots w_{n-1}) \]

不同阶数的语言模型

  • Unigram模型：

\[ P(s) = P(w_1)P(w_2)P(w_3) \dots P(w_n) \]

  • Bigram模型：

\[ P(s) = P(w_1)P(w_2 | w_1)P(w_3 | w_2) \dots P(w_n | w_{n-1}) \]

  • Trigram模型：

\[ P(s) = P(w_1)P(w_2 | w_1)P(w_3 | w_1 w_2) \dots P(w_n | w_{n-2} w_{n-1}) \]

  • K-gram模型：

\[ P(s) = P(w_1)P(w_2 | w_1)P(w_3 | w_1 w_2) \dots P(w_n | w_{n-k+1} \dots w_{n-1}) \]

具体例子

句子：我 今天 下午 打 羽毛球

\[\begin{aligned} p(\text{sentence}) &= p(\text{我，今天，下午，打，羽毛球}) \\ &=p(\text{我})p(\text{今天})p(\text{下午})p(\text{打})p(\text{羽毛球}) \implies 1-gram\\ &=p(\text{我})p(\text{今天} | \text{我})p(\text{下午} | \text{我})p(\text{打} | \text{下午})p(\text{羽毛球} | \text{打}) \implies 2-gram\\ &=p(\text{我})p(\text{今天} | \text{我})p(\text{下午} | \text{我，今天})p(\text{打} | \text{今天，下午})p(\text{羽毛球} | \text{下午，打}) \implies 3-gram \\ &=p(\text{我})p(\text{今天} | \text{我})p(\text{下午} | \text{我，今天})p(\text{打} | \text{我，今天，下午})p(\text{羽毛球} | \text{今天，下午，打}) \implies4-gram\\ &=p(\text{我})p(\text{今天} | \text{我})p(\text{下午} | \text{我，今天})p(\text{打} | \text{我，今天，下午})p(\text{羽毛球} | \text{我，今天，下午，打}) \implies 5-gram \end{aligned} \]

语言模型评价指标

困惑度（Perplexity）:

\[PP(s) = P(w_1, w_2, \dots, w_n)^{-\frac{1}{n}} = \sqrt[N]{\frac{1}{P(w_1, w_2, \dots, w_n)}} \]

句子概率过大，语言模型越好，困惑度越小。

NNLM模型->多分类任务

Input Label
None W1
W1 W2
W1,W2 W3
…… ……
W1,W2,..., Wn-1 Wn

NNLM(Feedforward Neural Net Language Model)

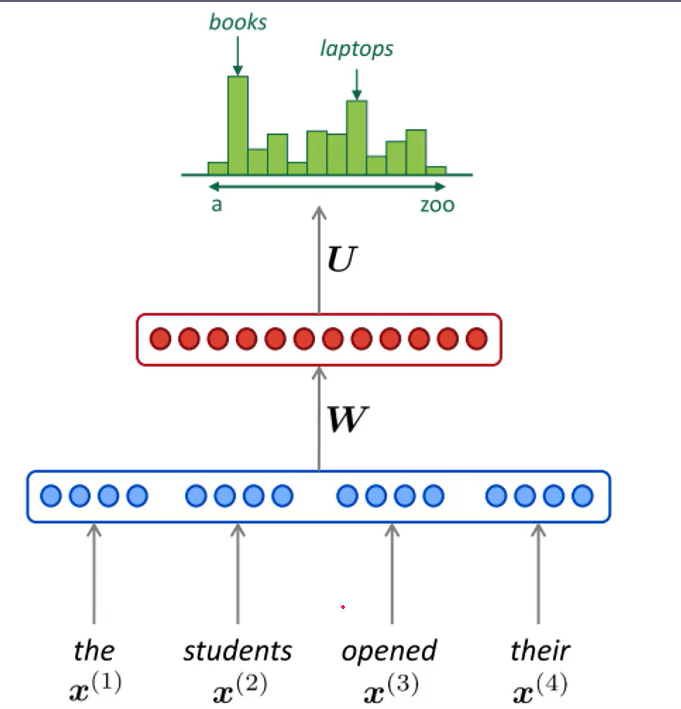
前向神经网络语言模型是一种无监督的（不需要标注语料），但是是监督训练，根据前\(n-1\)哥单词，预测第\(n\)个位置单词的概率（n-gram）。

通过word2id字典，字符->下标ID的映射，获得每个词的向量，然后做的是横向拼接（concat）。

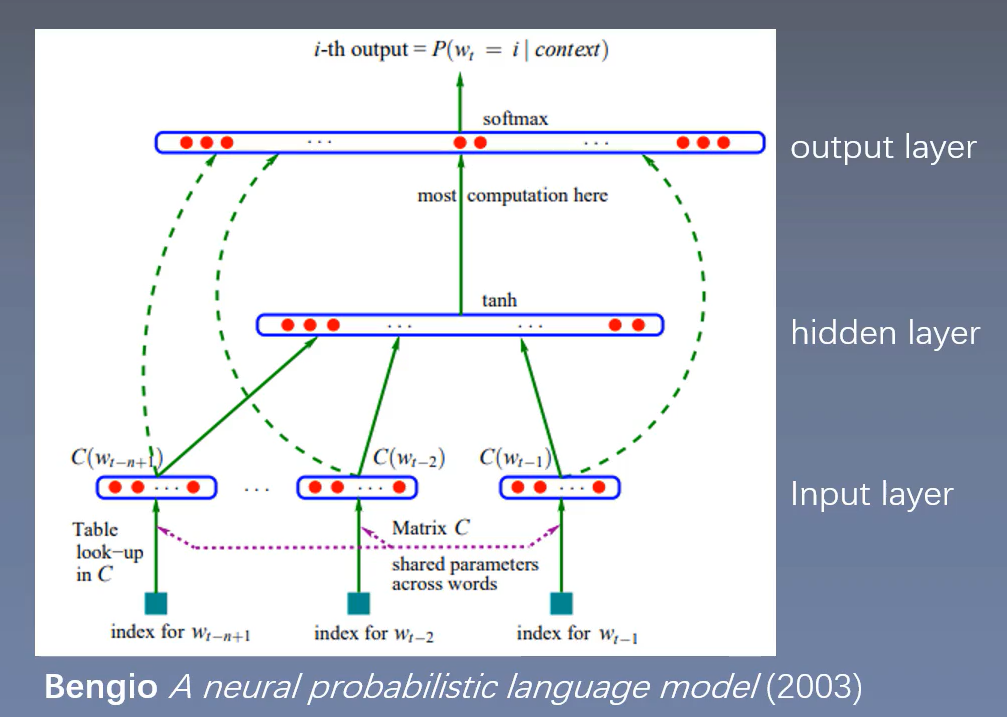
各个层介绍

输入层：将词映射成向量，相当于一个\(1 \times V\)的one-hot向量乘以一个\(V \times D\)的向量得到一个\(1\times D\)的向量。

\(n-1\)个相乘，则最终大小变成了\((n - 1) \times D\),

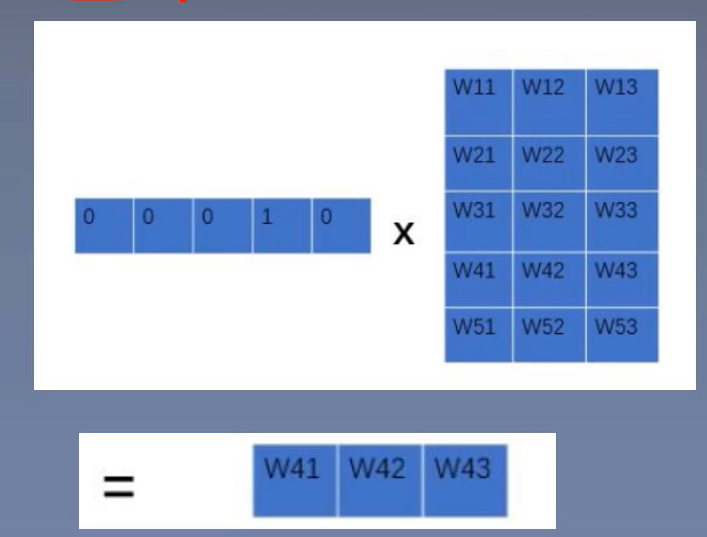
隐藏层：一个以\(\tanh\)为激活函数的全连接层：

\[a = \tanh(d+Ux) \]

输出层：一个全连接层，后面接一个softmax函数来生成概率分布。

\[y = Wa + b \]

其中y是一个\(1 \times V\) 的向量：

\[P(w_t|w_{t-n+1,\cdots, w_{t-1}}) = \dfrac{e^{y_{w_t}}}{\sum_ie^{y_i}} \]

softmax的两个性质：1. 代入值映射到0-1之间，2. 所有值和为1。

语言模型困惑度和Loss的关系

\[\begin{aligned} &\text{损失函数}: L = -\frac{1}{T} \sum_{i=1}^{T} \log p(w_i | w_{i-n+1}, \dots, w_{i-1}), 其中T是句子中词的个数\\ &\text{困惑度}: PP(s) = P(w_1, w_2, \dots, w_T)^{-\frac{1}{T}} = \sqrt[T]{\frac{1}{P(w_1, w_2, \dots, w_T)}} \\ &\log(PP(s)) = -\frac{1}{T} \log P(w_1) P(w_2 | w_1) \dots P(w_T | w_{T-n+1}, \dots, w_{T-1}) \\ &\log(PP(s)) = -\frac{1}{T} (\log P(w_1) + \log P(w_2 | w_1) + \dots + \log P(w_T | w_{T-n+1}, \dots, w_{T-1})) \\ &\log(PP(s)) = -\frac{1}{T} \sum_{i=1}^{T} \log p(w_i | w_{i-n+1}, \dots, w_{i-1}) \\ &\text{等价关系}: PP(s) = e^L \end{aligned} \]

统计语言模型还可以改进的地方

  1. 仅对一部分输出进行梯度传播
  2. 引入先验知识，如词性等
  3. 解决一词多义问题
  4. 加速softmax层

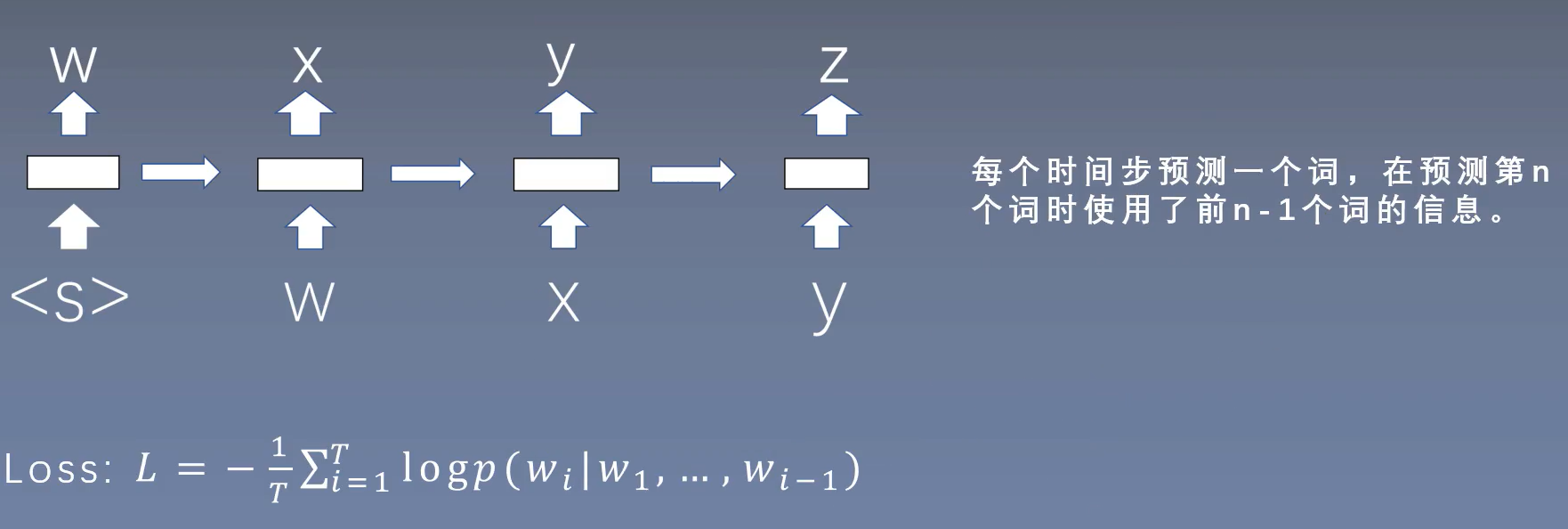
RNNLM(Recurrent Neural Net Language Model)

循环神经网络语言模型

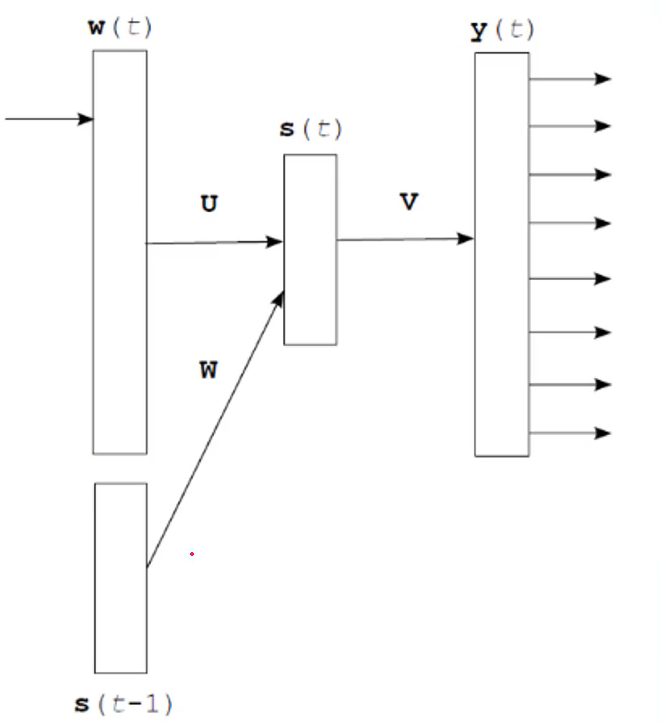
输入层：和NNLM一样，需要将当前时间步转化为词向量

隐藏层：对输入和上一个时间步的隐藏输出进行全连接层操作：\(s(t) = Uw(t)+Ws(t-1) + d\)

输出层：一个全连接层，后面接一个softmax函数来生成概率分布：

\[y(t) = b + V s(t) \]

其中y是一个\(1 \times V\)的向量：

\[P(w_t|w_{t-n+1,\cdots, w_{t-1}}) = \dfrac{e^{y_{w_t}}}{\sum_ie^{y_i}} \]

Word2Vec

Word2Vec基本思想：

句子中相近的词之间是有联系的，比如今天后面经常出现上午，下午和晚上。所以Word2vec的基本思想就是用词来预测词。

skip-gram：使用中心词预测周围词。

cbow：使用周围词预测中心词。

Skip-gram模型

基于窗口的使用中心词预测周围词

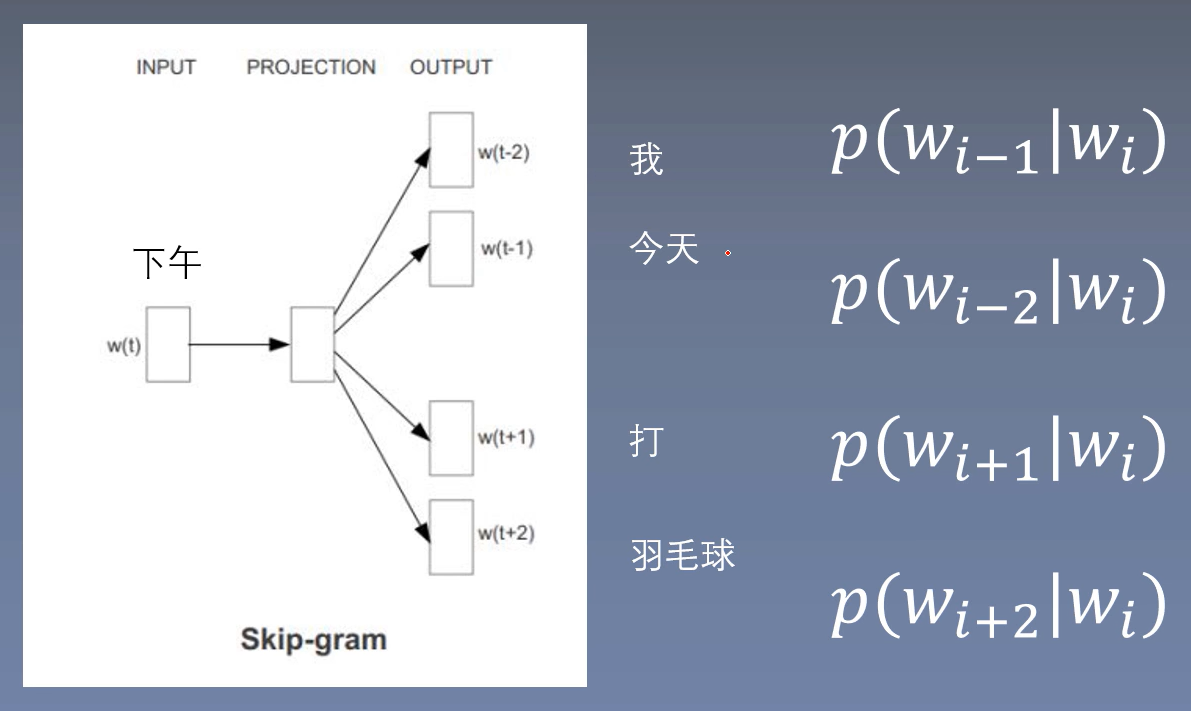
\(input: w_i\)
\(label: w_{i-1}\)

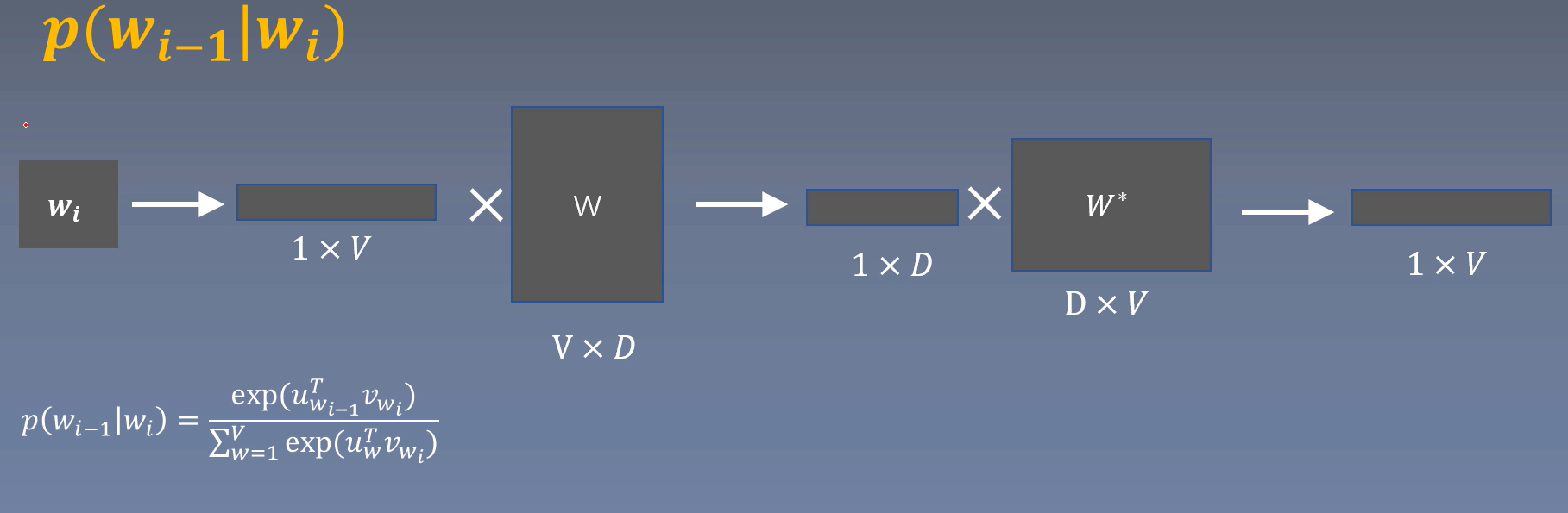
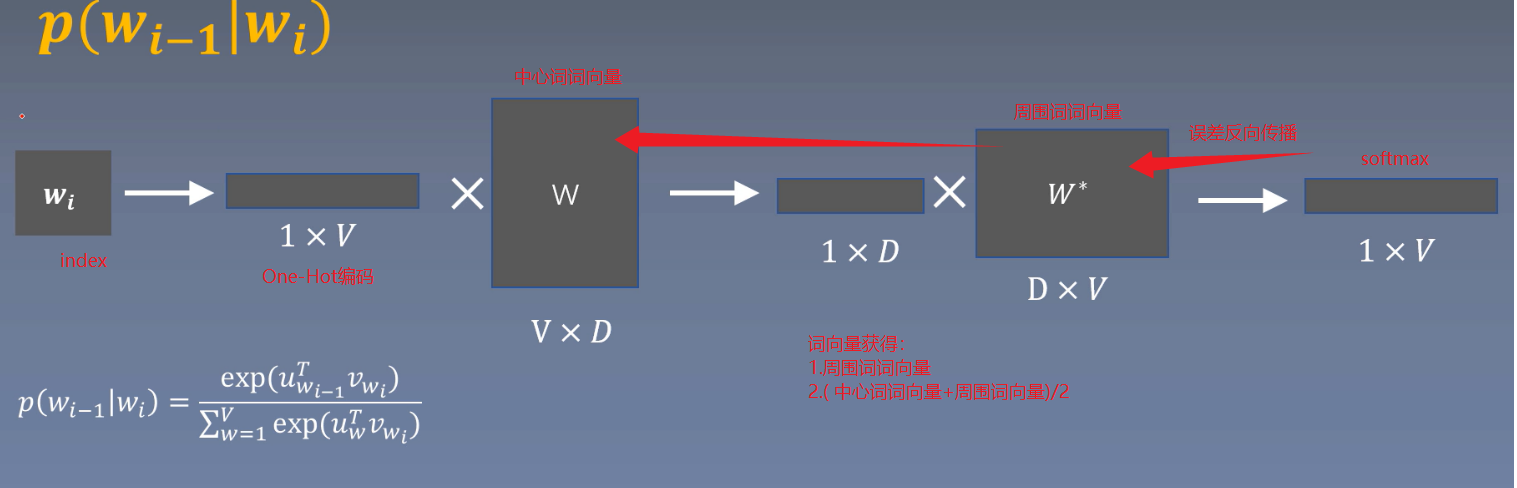
Skip-gram损失函数：

\[J(\theta) = \frac{1}{T} \sum_{t=1}^{T} \sum_{\substack{-m \le j \le m , j \ne 0}} \log p(w_{t+j} | w_t) \]

求最大值，损失的话，添加负号，越小越好。

CBOW原理

Continuous Bag-of-Words

周围词预测中心词

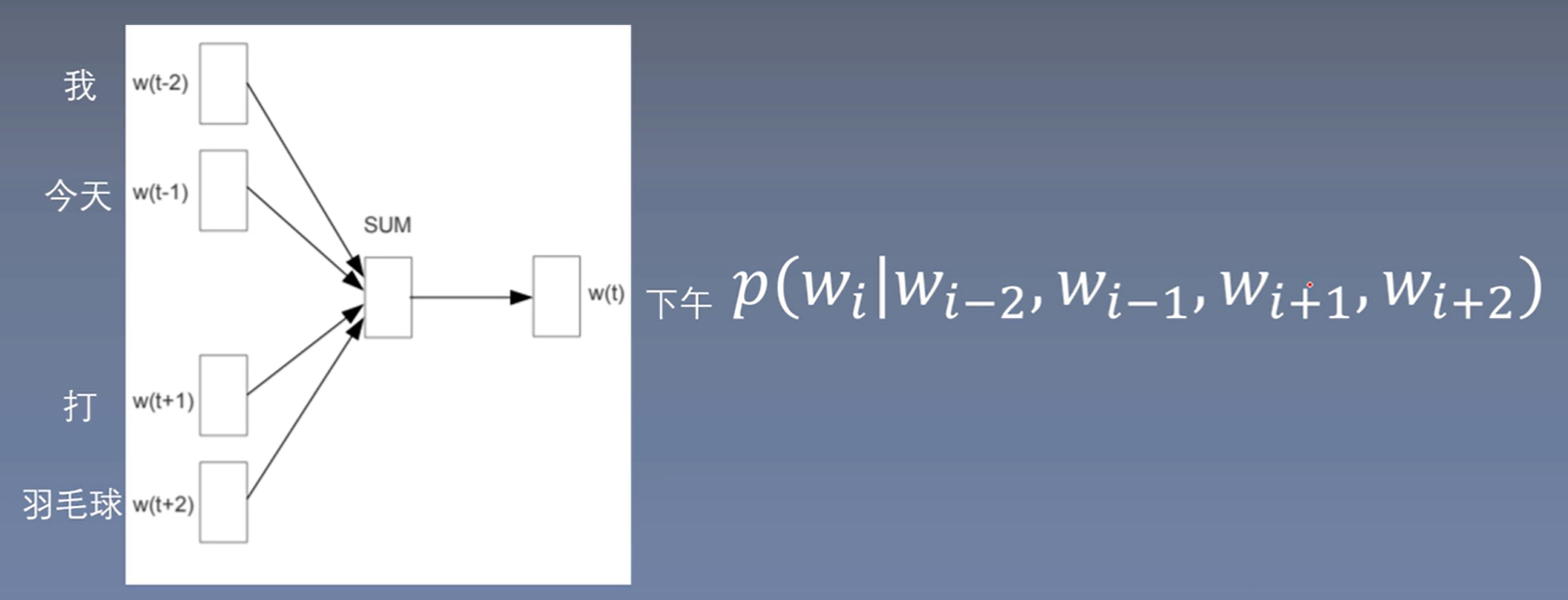
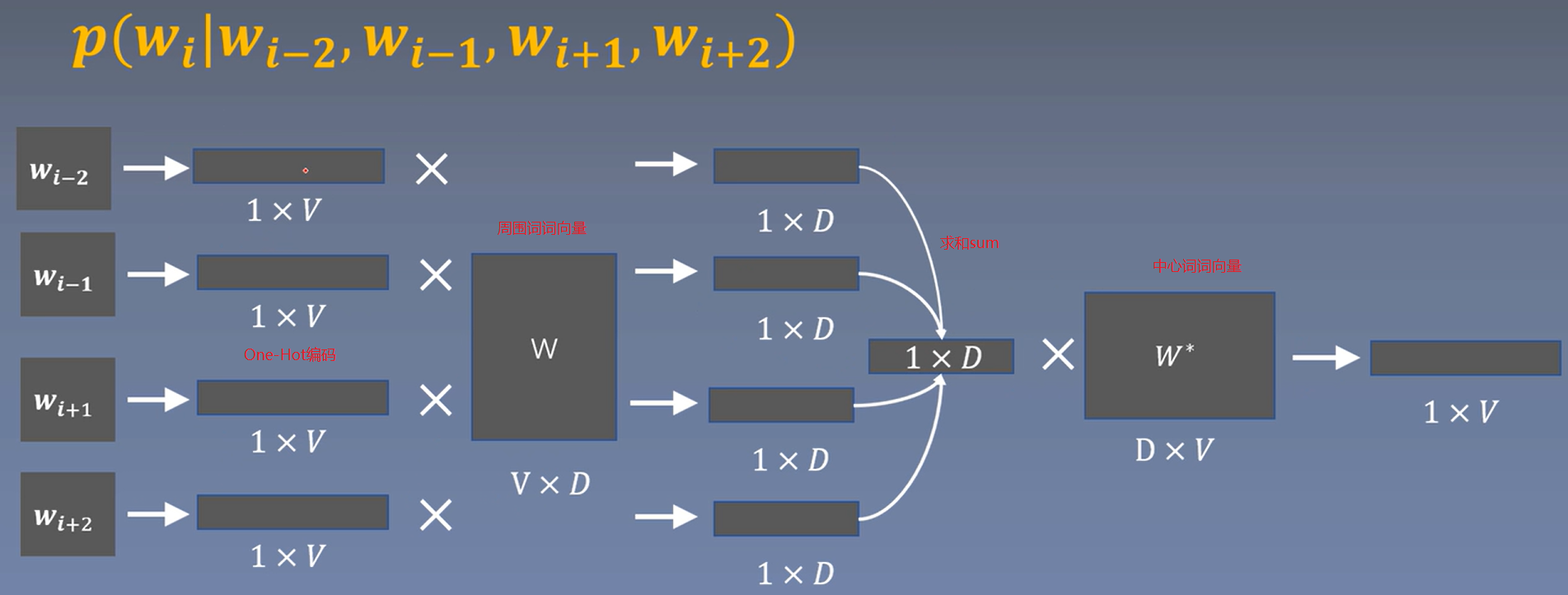
CBOW损失函数 \(J(\theta)\) 的数学表达式为：

\[J(\theta) = \frac{1}{T} \sum_{T} \log P(c|o) = \frac{1}{T} \sum \frac{\exp\{u_o^T v_c\}}{\sum_{j=1}^{V} \exp\{u_o^T v_j\}} \]

公式说明：

  1. 符号含义：
  • \(T\): 语料库中的总词数
  • \(c\): 中心词
  • \(o\): 上下文词窗口（包含多个上下文词）
  • \(u_o\): 上下文词窗口的向量表示，计算为窗口内所有上下文词向量的和，即 \(u_o = \text{sum}(e_1, e_2, e_3, e_4)\)
  • \(v_c\): 中心词的向量表示
  • \(v_j\): 词汇表中第 \(j\) 个词的向量表示
  • \(V\): 词汇表的总词数
  1. 计算逻辑：
  • 外层求和（\(\sum_{T}\)）遍历语料库中每个中心词和其对应的上下文窗口
  • 对每个中心词 \(c\) 和其上下文窗口 \(o\)，计算条件概率 \(P(c|o)\)
  • 条件概率 \(P(c|o)\) 使用 softmax 函数计算，其中分子是上下文窗口向量 \(u_o\) 和中心词向量 \(v_c\) 的点积的指数，分母是所有词向量与上下文窗口向量点积的指数之和
  • 对每个条件概率取对数，然后取平均（除以 \(T\)）

我自己的理解：

为什么把\(u_o^T v_c\)做内积呢？我的理解就是余弦相似度，这里的中心词和周围词其实可以当成两个差不多的词典，我们可以认为每一行代表一个词向量，两个词典的这一行都差不多，当两者内积，代入softmax，概率越高，说明相似度越高，这些词更相近。

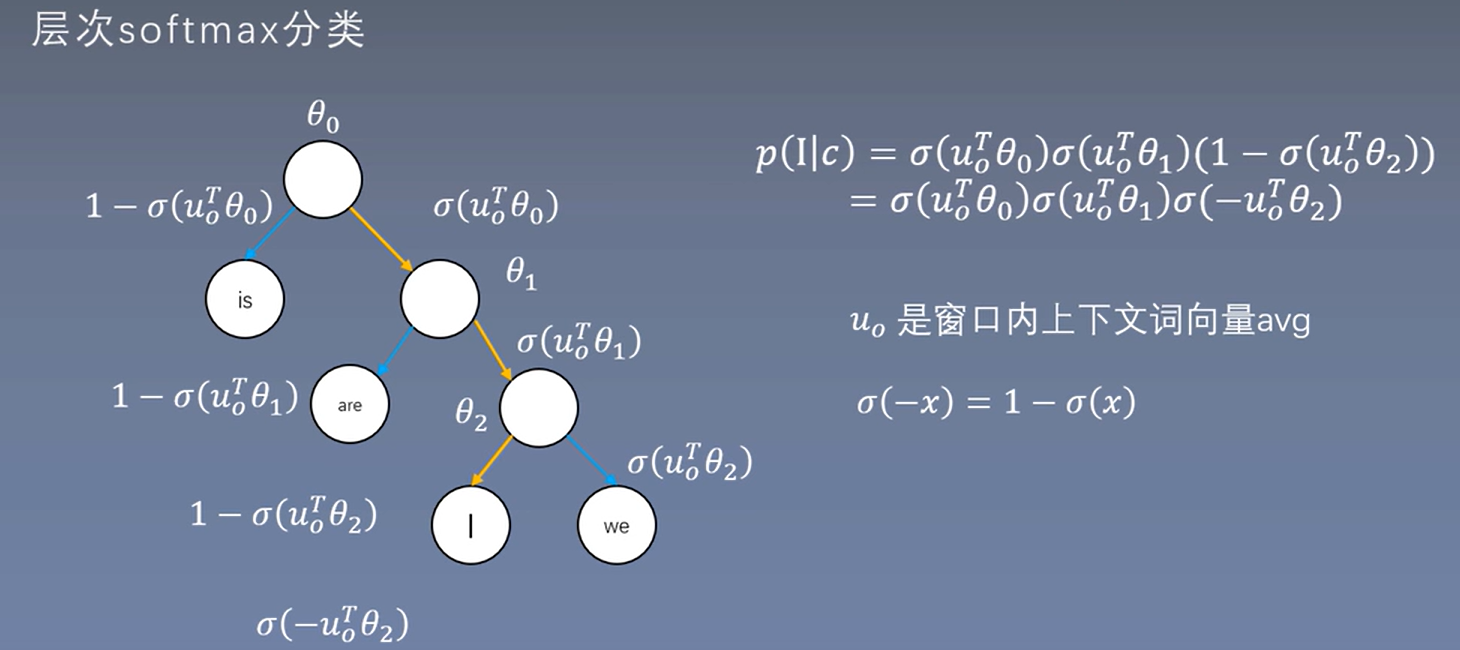
层次Softmax（不理解，目前还没弄懂）

\[P(c|o) = \frac{\exp\{u_o^T v_c\}}{\sum_{j=1}^{V} \exp\{u_o^T v_j\}} \]

Softmax对于要输出V个概率，由于通常V比较大，计算复杂度高，所以如果降低复杂度呢？方法一，层次softmax

疑问：为啥用二叉树替代，sigmoid代替softmax，为什么能替代。

核心： softmax-------> sigmoid

\[\dfrac{e^x}{\sum e^x} \implies \dfrac{1}{1+e^{-x}} \]

多个指数计算，变成一个指数运算。

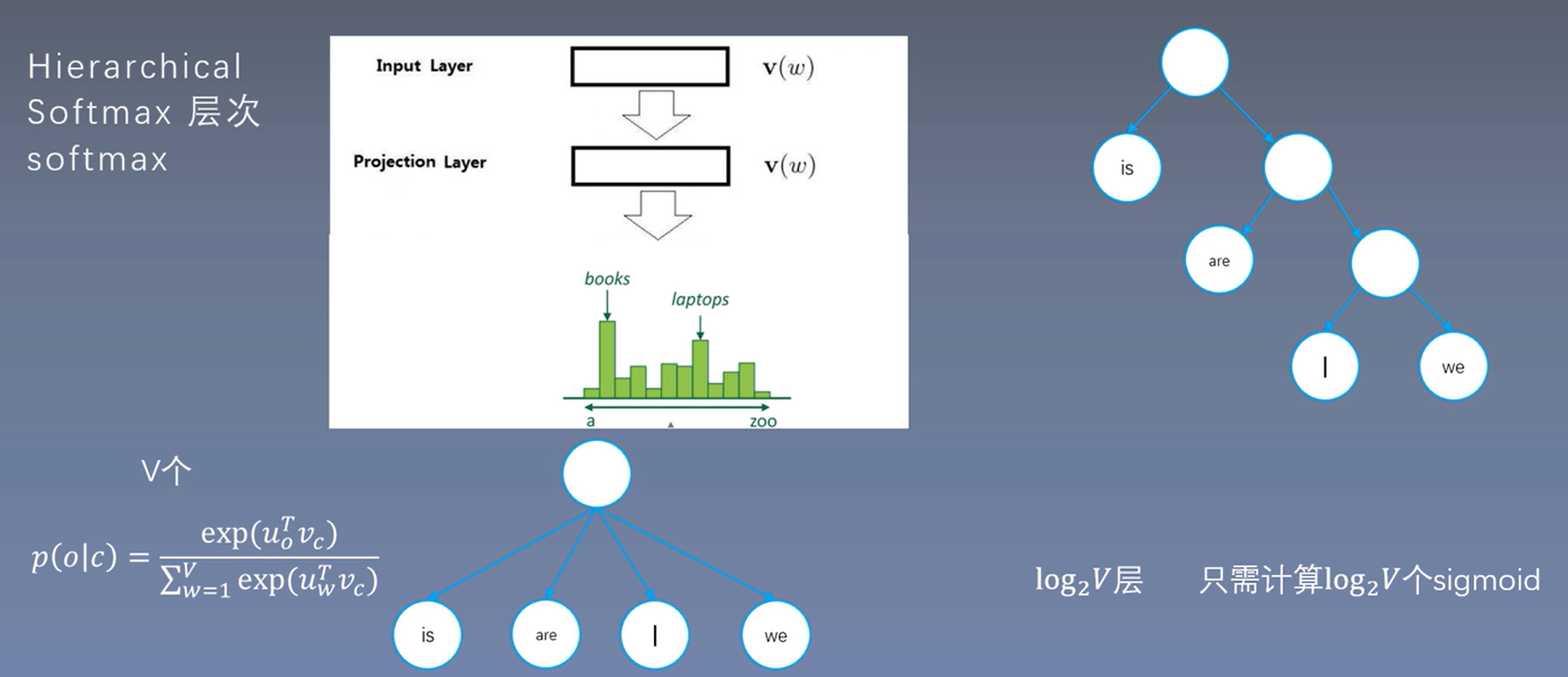
层次softmax只需计算\(\log_2V\)个sigmoid

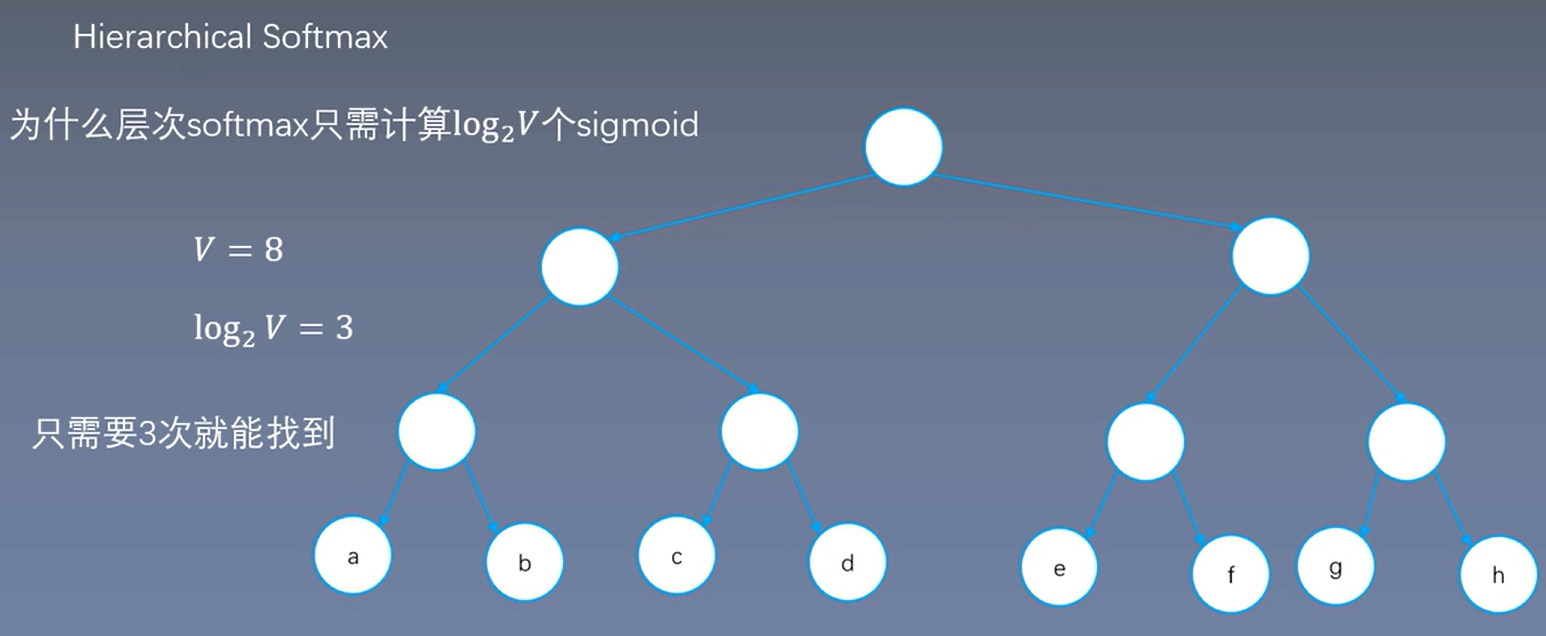
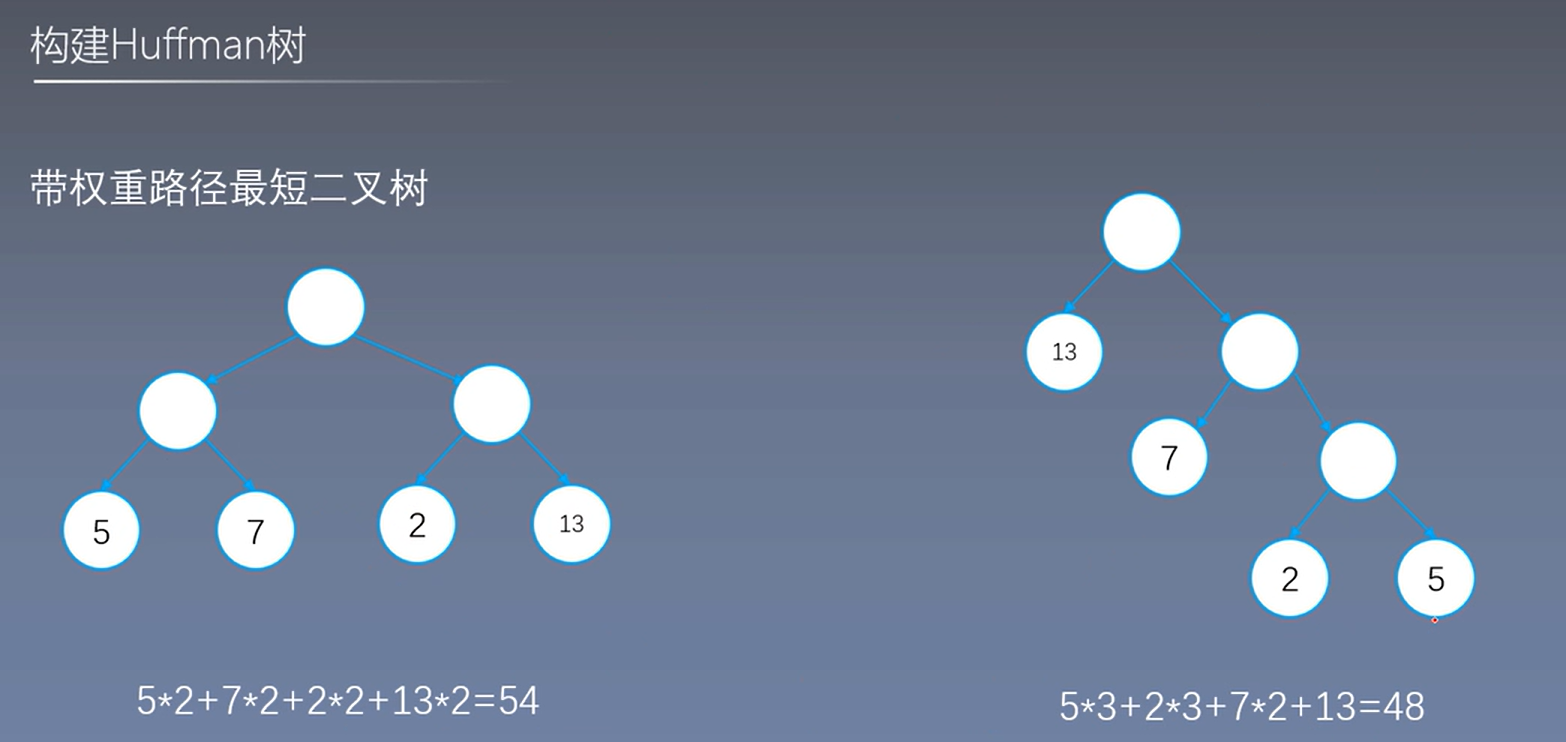
满二叉树->哈夫曼树， 计算次数减少

层次softmax构建方法

skip-gram构建


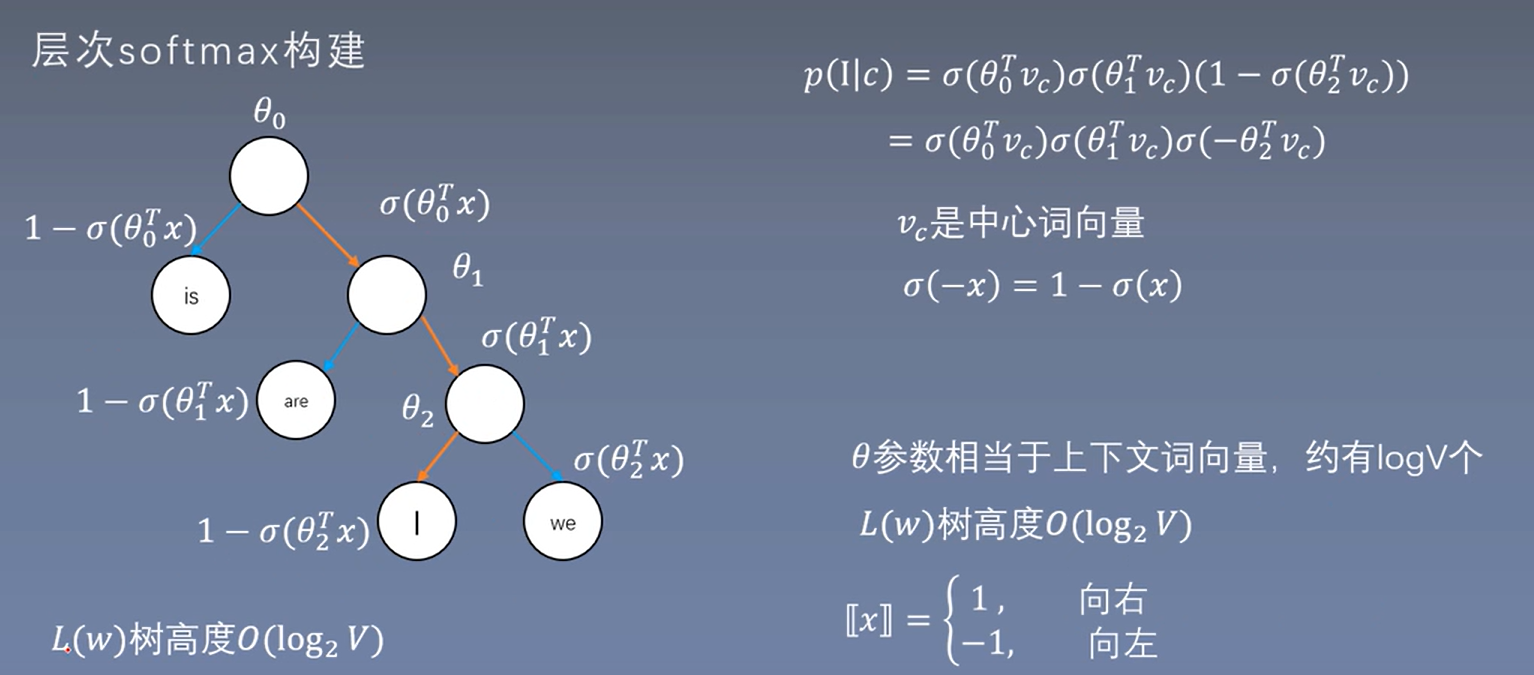
cbow构建

这里的一个重点是\(u_0\)是原来的词向量，而\(\theta\)不再是原来的词向量了

Negative Sampling（负采样）

舍弃多分类，提升速度

一开始的训练方法

训练方法

  • 滑动窗口
  • 预测方式：
    • 中间向两侧，从某个中心点开始，逐渐向外扩展上下文来进行训练，有助于模型先把握文本的局部结构和语境。
    • 两侧向中间，是从文本的开头和结尾同时向中间推进，这种策略能让模型更快地捕捉到文本的整体结构和长距离依赖关系。

训练过程

（1）输入的数据格式

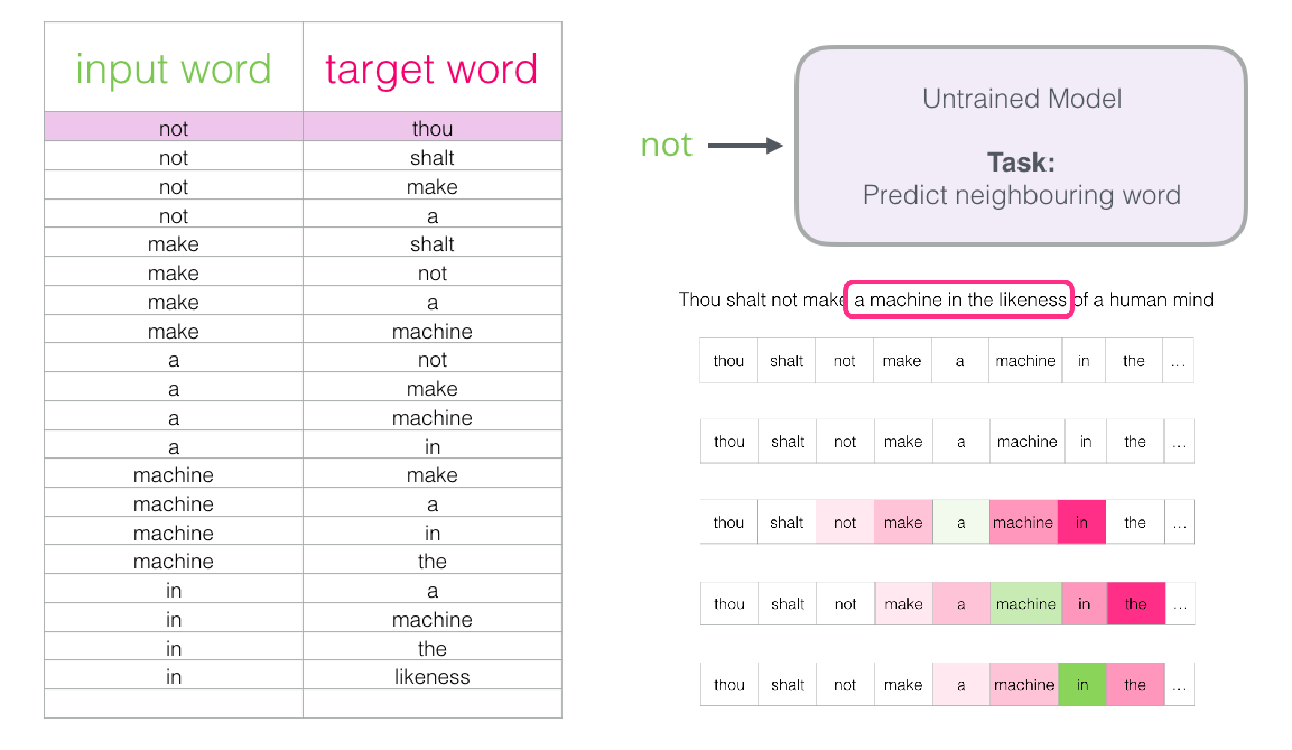
（2）语言模型的流程

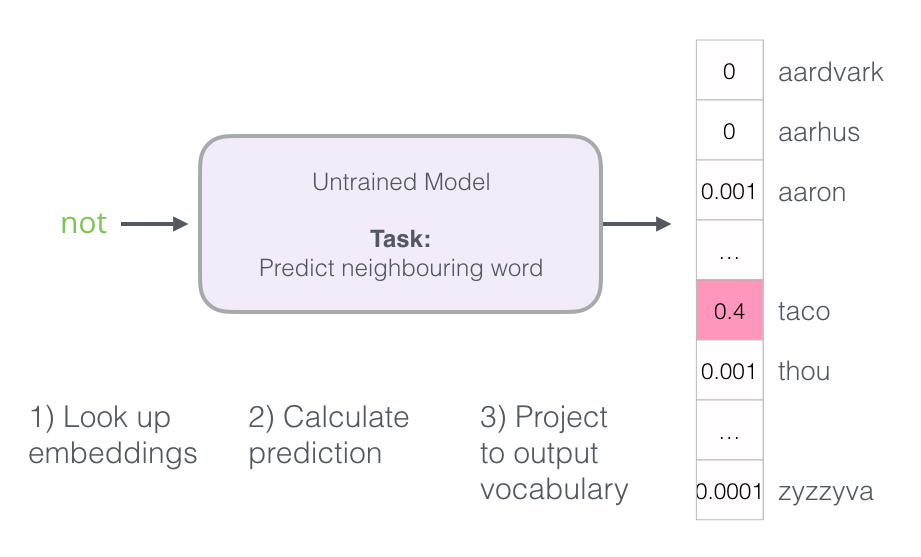
（3）BP损失的回传，参数调整更新，最终训练出词汇表。

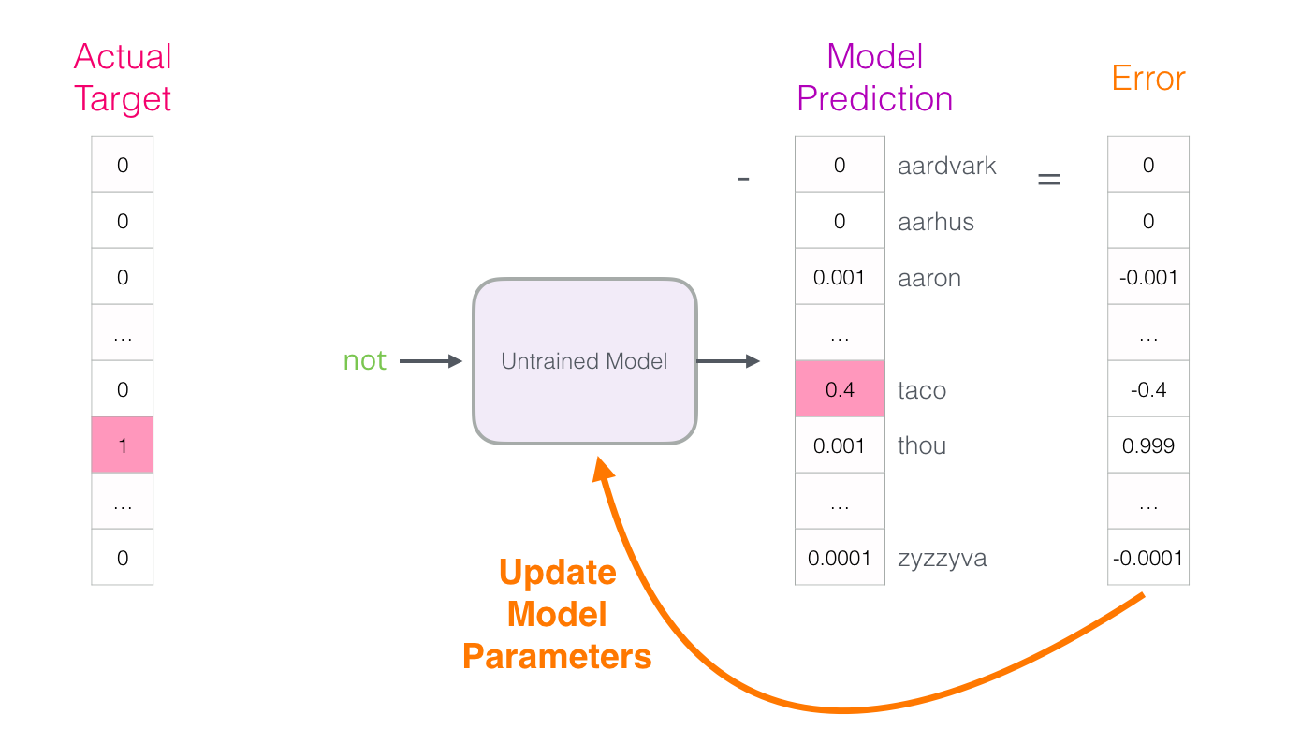
最终词典太大，转换一种思路

一种方法是将目标分为两个步骤：

1.生成高质量的词嵌入（不要担心下一个单词预测）。

2.使用这些高质量的嵌入来训练语言模型（进行下一个单词预测）。

负采样方法

要使用高性能模型生成高质量嵌入，我们可以改变一下预测相邻单词这一任务：

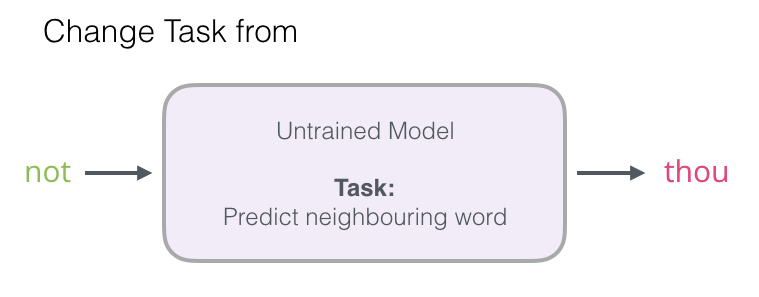
将其切换到一个提取输入与输出单词的模型，并输出一个表明它们是否是邻居的分数（0表示“不是邻居”，1表示“邻居”）。

这个简单的变换将我们需要的模型从神经网络改为逻辑回归模型——因此它变得更简单，计算速度更快。

这个开关要求我们切换数据集的结构——标签值现在是一个值为0或1的新列。它们将全部为1，因为我们添加的所有单词都是邻居。

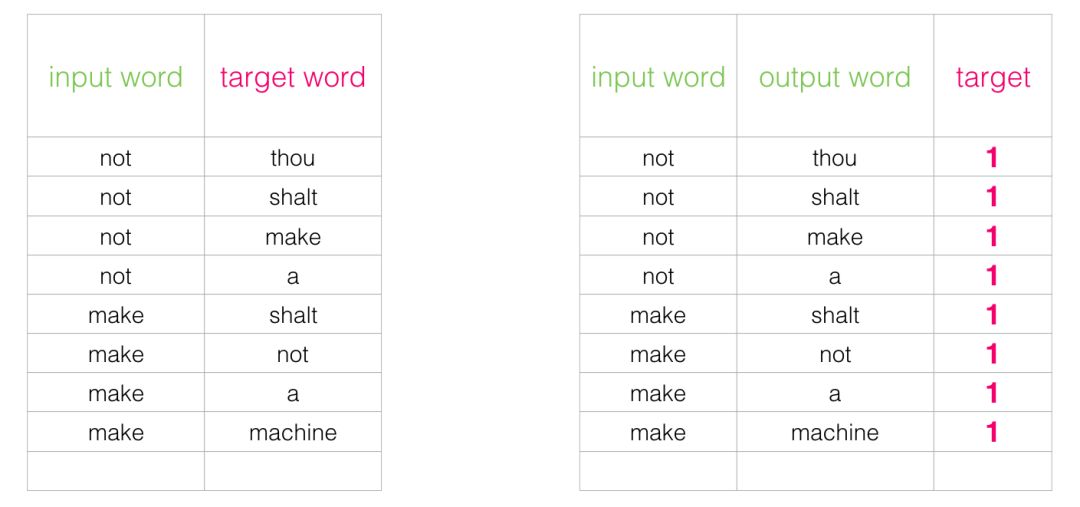
现在的计算速度可谓是神速啦——在几分钟内就能处理数百万个例子。但是我们还需要解决一个漏洞。如果所有的例子都是邻居（目标：1），我们这个”天才模型“可能会被训练得永远返回1——准确性是百分百了，但它什么东西都学不到，只会产生垃圾嵌入结果。

为了解决这个问题，我们需要在数据集中引入负样本 - 不是邻居的单词样本。我们的模型需要为这些样本返回0。模型必须努力解决这个挑战——而且依然必须保持高速，这就是负向采样。

对于我们数据集中的每个样本，我们添加了负面示例。它们具有相同的输入字词，标签为0。

但是我们作为输出词填写什么呢？我们从词汇表中随机抽取单词。

谈到这里，我们就可以分析一下负向采样的复杂度优势了，由于最终变成了二分类，对于每个词，一次要输出一个概率，负向采样k个词，加上最后输出概率的一个分子，总共k+1次指数操作。K<<V.
由于周围词向量和中心词向量都是完整的\(V\times D\),所以参数量肯定要比层次softmax多。
k要小于\(\log_2V\)，所以负向采样比softmax快。

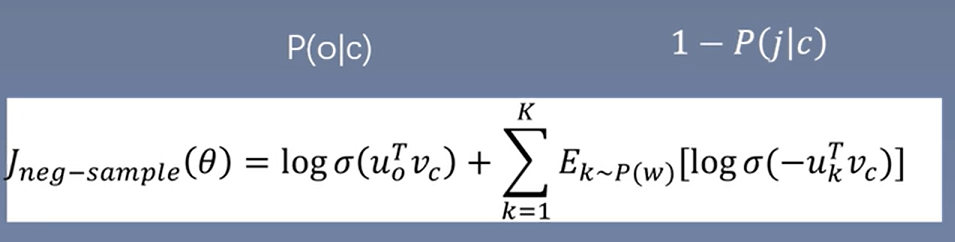
采样方法

区别于随机采样的另一种，指数为\(x^{\frac{3}{4}}\)的指数函数，求导为\(x^{-\frac{1}{4}}\),导函数为单调递减函数，达到减少频率大的词的抽样频率，增加频率小的词的抽样频率。

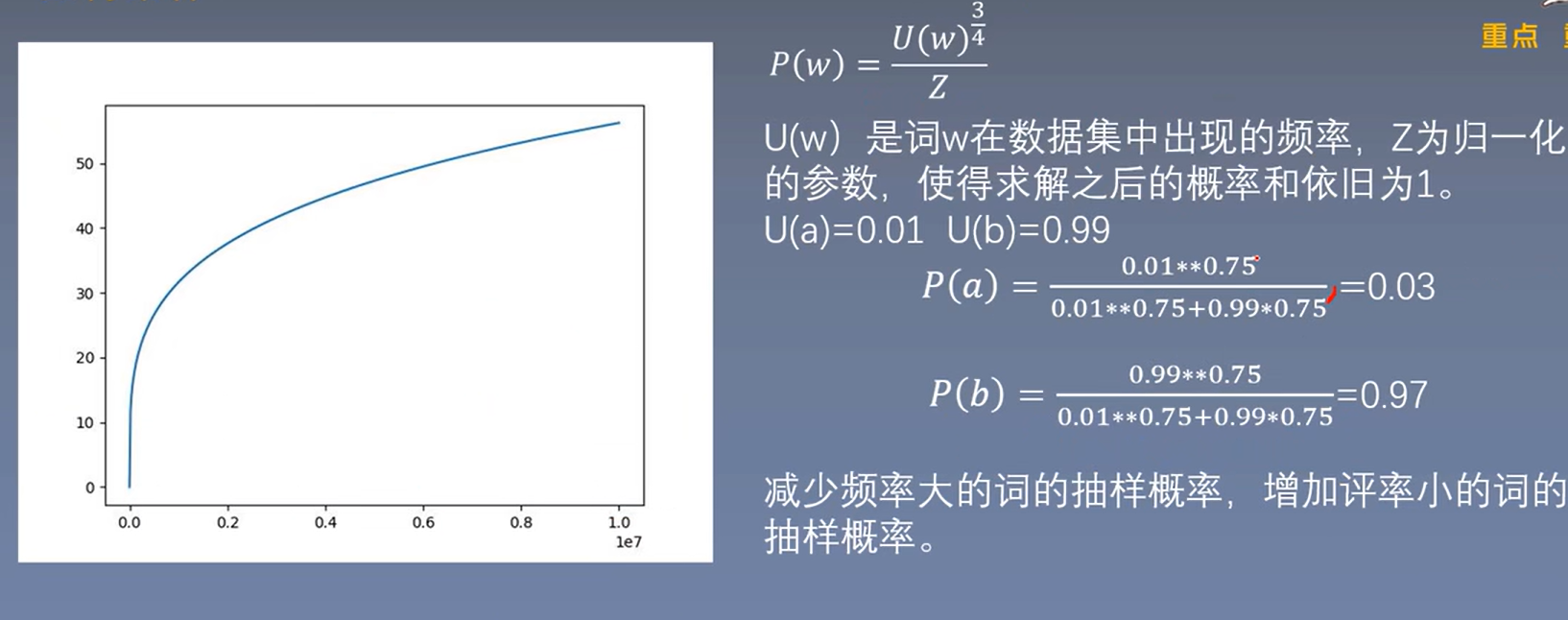
重采样：Subsampling of Frequent words

自然语言处理共识：文档或者数据集中出现频率高的词往往携带信息较少，比如the, is, a, and, 而出现频率低的词往往携带信息多。

什么是青蛙？

  1. 什么是深度学习，什么是CNN，什么是RNN，这篇告诉你。

  2. 青蛙（Frog）属于脊索动物门、两栖纲、无尾目、蛙科的两栖类动物，成体无尾，卵产于水中。

重采样的原因：

  • 想更多地训练重要的词对，比如训练“France”和“Paris”之间的关系比训练“France”和“the”之间的关系要有用。
  • 高频词很快就训练好了，而低频次需要更多的轮次。

重采样方法：

\[P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} \]

其中\(f(w_i)\)为词\(w_i\)在数据集中出现的频率。文中\(t\)选取为\(10^{-5}\)，训练集中的词\(w_i\)会以\(P(w_i)\)的概率被删除。

重采样的分析：

\[P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} \]

词频越大，\(f(w_i)\)越大，\(P(w_i)\)越大，那么词\(w_i\)就有更大的概率被删除，反之亦然。如果词\(w_i\)的词频小于等于\(t\)，那么\(w_i\)则不会被删除。

优点：加速训练，能够得到更好的词向量。

总结来说:

word2vec就是2+3， 2+2+1

两个模型：（1）skip-gram:中心词预测周围词；（2）cbow:周围词预测中心词，周围词的平均预测中心词

两种加速训练的方法：（1）层次softmax，将softmax转化为多次sigmoid，用哈夫曼树加速训练；（2）负采样，将多分类问题转换为二分类问题，其中正样本就是一个周围词和一个中心词就是正样本，一个中心词和随机采样周围词就是负样本。

一个技术： 采样技巧：（1）重采样，把高频词删去一些，低频词保留一些，训练加快。

模型的结果

RNNLM, NNLM，CBOW，Skip-gram模型比较

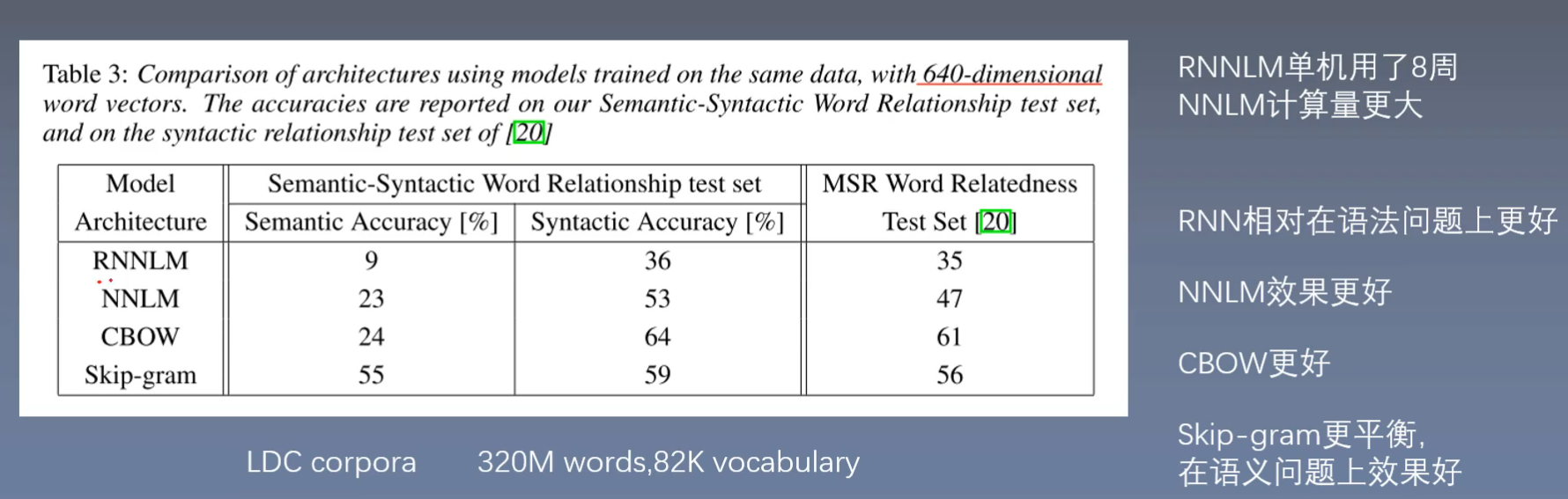
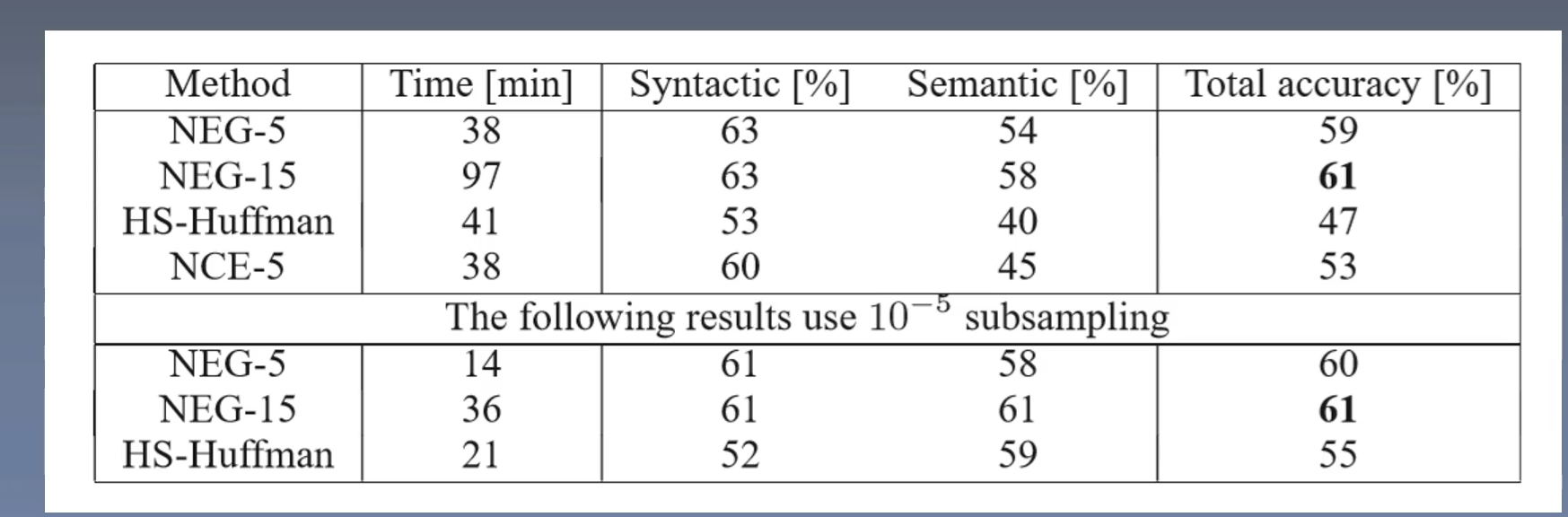
HS（层次softmax）, NEG（负采样）对比

posted @ 2025-03-10 15:43  哲远甄骏  阅读(49)  评论(0)    收藏  举报