谱聚类（spectral clustering）原理总结

1. 谱聚类（spectral clustering）原理总结

转载借鉴出处

谱聚类概述

\(\quad\quad\)谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用，它的主要思想是把所有的数据看做空间中的点， 这些点之间可以用边连接起来。聚类较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后的不同的子图间的边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

\(\quad\quad\)谱聚类的原理很简单，但是理解这个算法，需要掌握一定的图论和线性代数等相关知识，其中涉及的谱聚类基础如下：

• 无向权重图
• 相似矩阵
• 拉普拉斯矩阵
• 无向图切图

无向权重图

\(\quad\quad\)由于谱聚类是基于图论的， 需要我们首先了解一下图的概念。

\(\quad\quad\)对于一个图\(G\)< 我们一般用点的集合\(V\)和边的集合\(E\)来描述。即为\(G(V,E)\)。其中\(V\)即为数据集里所有的点的集合\((v_1, v_2,\cdots,v_n)\)。对于\(V\)中的任意两个点，可以有边连接，也可以没有边连接。我们定义权重\(w_{ij}\)为点\(v_i\)和\(v_j\)之间的权重，由于这里讨论的图是无向图，所以有\(w_{ij} = w_{ji}\)。

\(\quad\quad\)对于有边连接的两个点\(v_i\)和\(v_j\)，\(w_{ij} > 0\)，由于没有边连接的两个点\(v_i\)和\(v_j\), \(w_{ij} = 0\)。对于图中的任意一个点\(v_i\)，它的度\(d_i\)定义为和它相连的所有边的权重之和，即

\[d_i=\sum\limits_{j = 1}^{n}w_{ij} \]

\(\quad\quad\)利用每个点度的定义，我们可以得到一个\(n \times n\)的度矩阵\(D\),它是一个对角矩阵，只有主对角线有值，对应第\(i\)行的第\(i\)个点的度数，定义如下：

\[D = \left[ \begin{array}{ccc} d_1 & \cdots & \cdots \\ \cdots & d_2 & \cdots \\ \vdots & \vdots & \ddots \\ \cdots & \cdots & d_n \end{array} \right] \]

\(\quad\quad\)利用所有点之间的权重值，我们可以得到图的邻接矩阵\(W\)， 它也是一个\(n \times n\)的矩阵，第\(i\)行的第\(j\)个值对应的权重\(w_{ij}\)。

\(\quad\quad\)除此之外，对于点集\(V\)的一个子集\(A \subset V\),定义：

\[\mid A \mid :=子集A中点的个数\\ vol(A):=\sum\limits_{i \in A} d_i \]

相似矩阵

\(\quad\quad\)对于邻接矩阵\(W\)， 它是由任意两点之间的权重值\(W_{ij}\)组成的矩阵。通常可以自己输入权重，但是在谱聚类中，只有数据点的定义，并没有直接给出这个邻接矩阵，如何获得这个邻接矩阵呢？

\(\quad\quad\)基本思想是，距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，不过这仅仅是定性，我们需要定量的权重值， 一般来说，可以通过样本点距离度量的相似矩阵\(S\)来获得邻接矩阵\(W\)。

\(\quad\quad\)构建邻接矩阵\(W\)的方法有三类

• \(\epsilon -\)近邻法
• K邻近法
• 全连接法

\(\epsilon -\)近邻法

\(\quad \quad\) 对于\(\epsilon -近邻法\)，它设置了一个距离阈值\(\epsilon\)， 然后采用欧式距离\(s_{ij}\)度量任意两点\(x_i\)和\(x_j\)的距离。即相似矩阵\(s_{ij} = \mid\mid x_i - x_j \mid\mid_{2}^{2}\), 然后根据\(s_{ij}\)和\(\epsilon\)的大小关系，来定义邻接矩阵\(W\)如下：

\[w_{ij}= \begin{cases} 0 & s_{ij} > \epsilon \\ \epsilon & s_{ij} < \epsilon \end{cases} \]

\(\quad \quad\) 从上式可见，两点间的权重要不就是\(\epsilon\)，要不就是0, 没有其他的信息了。距离远近度量很不准确，因此在实际应用中， 我们很少使用\(\epsilon-\)邻近法。

k邻近法

\(\quad\quad\) 利用knn算法遍历所有的样本点，取每个样本最近的k个点作为近邻， 只有和样本距离最近的k个点之间的\(w_{ij} > 0\)。但是这种方法会造成重构之后的邻接矩阵\(W\)非对称，后面的算法需要用到对称邻接矩阵。为了就解决这种问题，一般采取下面两种方法：

• 第一种就是K邻近法是只要一个点在另一个点的K近邻中，则保留\(s_{ij}\)

\[w_{ij} = w_{ji} = \begin{cases} 0 & x_i\notin KNN(x_j) ~and~x_j\notin KNN(x_i)\\ exp(-\dfrac{\mid \mid x_i - x_j \mid \mid}{2\sigma^2}) & x_i\in KNN(x_j) ~or~x_j\in KNN(x_i) \end{cases} \]

• 第二种就是K邻近法是必须两个点互为K近邻中，才能保留\(s_{ij}\)

\[w_{ij} = w_{ji} = \begin{cases} 0 & x_i\notin KNN(x_j) ~or~x_j\notin KNN(x_i)\\ exp(-\dfrac{\mid \mid x_i - x_j \mid \mid}{2\sigma^2}) & x_i\in KNN(x_j) ~and~x_j\in KNN(x_i) \end{cases} \]

全连接法

\(\quad \quad\) 全连接法相比前两种方法，第三种方法所有的点之间的权重值都大于0，因此称之为全连接法， 可以选择不同的核函数来定义边权重，常用的有多项式核函数， 高斯核函数和Sigmoid核函数， 最常用的是高斯核函数RBF, 此时相似矩阵和邻接矩阵相同：

\[w_{ij} = s_{ij} = exp(-\dfrac{\mid \mid x _i - x_j \mid \mid _2^2}{2\sigma^2}) \]

\(\quad \quad\) 在实际的应用中， 使用第三种全连接法来建立邻接矩阵是最普遍的，而在全连接法中使用高斯核函数RBF是最普遍的。

全连接法涉及的核函数

借鉴网站

核函数定义

• 将原始空间中的向量作为输入向量，并返回特征空间（转换后的数据空间,可能是高维）中向量的点积的函数称为核函数。

线性核函数

核函数表达式为：

\[k(x_i, x_j) = x_i^T x_j \]

\(\quad \quad\)其实就是对两个向量做内积。

多项式核函数（Polynomial kernel function）

核函数表达式为：

\[K(x_i, x_j) = (\zeta + \gamma x_i^Tx_j)^Q \]

\(\quad \quad\)其中多项式中，\(\gamma\)就是用来对内积进行缩放的，而\(\zeta\)就是一个常数项，来进行加减上的调整，\(Q\)则是控制次数的。

\(\quad \quad\)当\(\zeta\)为0， \(\gamma\)为1， \(Q\)为1， 就会得到线性核函数即\(x_i^Tx_j\)。

高斯核函数

\(\quad \quad\)提到高斯，会联想到高斯分布(正态分布)，一维高斯分布公式是这样：

\[f(x) = \dfrac{1}{\sqrt{2\pi\sigma}}exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) \]

图线是这样：

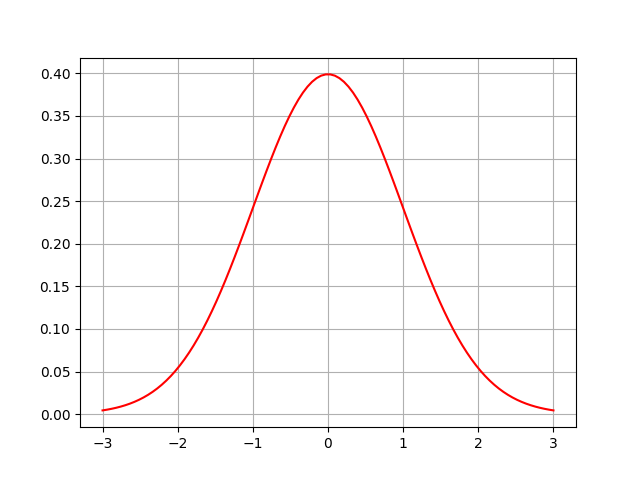
\(\quad \quad\)上面对高斯分布的图像有了大概了解了， 接下来引出高斯核函数：

\[K(x_i, x_j) = exp(\dfrac{\mid \mid x_i - x_j \mid \mid ^2}{2\sigma^2}) \]

分析高斯核函数

• 首先抛开\(\sigma\)

对高斯核函数进行展开， 首先忽略掉分母\(2\sigma\)的平方，可以得到：

\[\begin{align} K(x_i, x_j) &= exp(-\mid \mid x_i - x_j \mid \mid ^2) \notag \\ &=exp(-x_i^2 -x_j^2+2x_ix_j) \notag \\ &=exp(-x_i^2)\cdot exp(-x_j^2) \cdot exp(2x_ix_j) \end{align} \]

其中\(exp(2x_ix_j) = \sum\limits_{n = 0}^{\infty}\dfrac{(2x_ix_j)^n}{n!} = \sum\limits_{n = 0}^{\infty}\sqrt{\dfrac{2^n}{n!}} \sqrt{\dfrac{2^n}{n!}} (x_i)^n (x_i) ^n\),

泰勒展开后，原式化为：

\[\sum\limits_{n = 0}^{\infty}exp(-x_i^2)\sqrt{\dfrac{2^n}{n!}}(x_i)^n\cdot \sum\limits_{n = 0}^{\infty}exp(-x_i^2)\sqrt{\dfrac{2^n}{n!}}(x_i)^n \]

整理最后为：\(K(x_i, x_j) = \phi(x_i)^T \phi(x_j)\),其中\(\phi(x) = e^{-x^2}(1 + \sqrt{\dfrac{2}{1!}}+\sqrt{\dfrac{2^2}{2!}}+ \cdots +\sqrt{\dfrac{2^n}{n!}})\)

观察上式，可以发现，高斯核函数可以把传入的\(x_i和x_j\)都可以扩展到无穷大的维度上。

• 单独分析\(\sigma\)

\[K(x_i, x_j) = exp(\dfrac{\mid \mid x_i - x_j \mid \mid ^2}{2\sigma^2}) \]

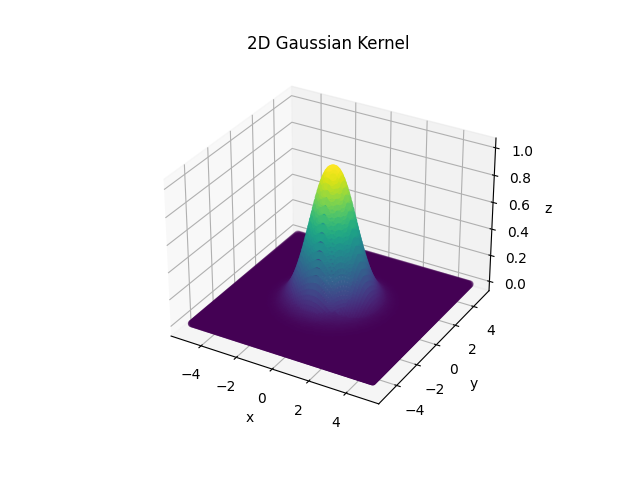
当\(\sigma = 1\),图像如下所示

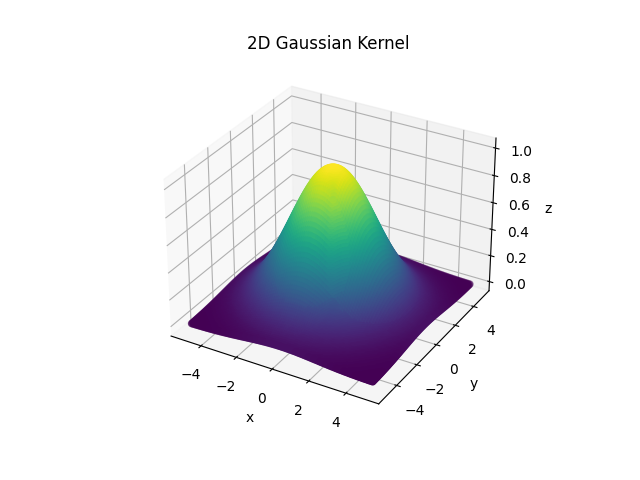
当\(\sigma = 2\),图像如下所示

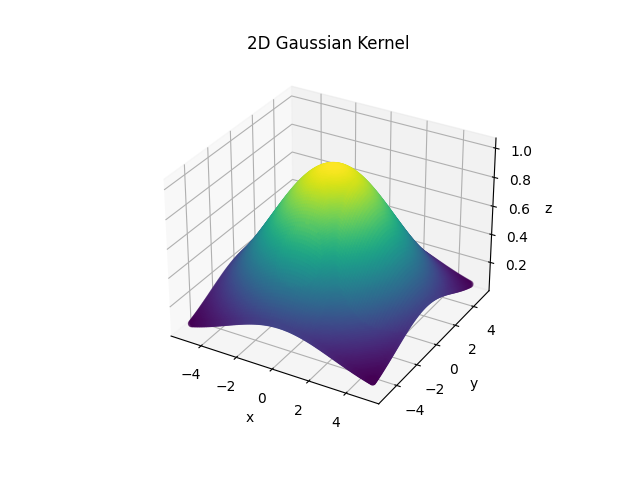
当\(\sigma = 3\),图像如下所示

当\(\sigma\) = 0.2时，

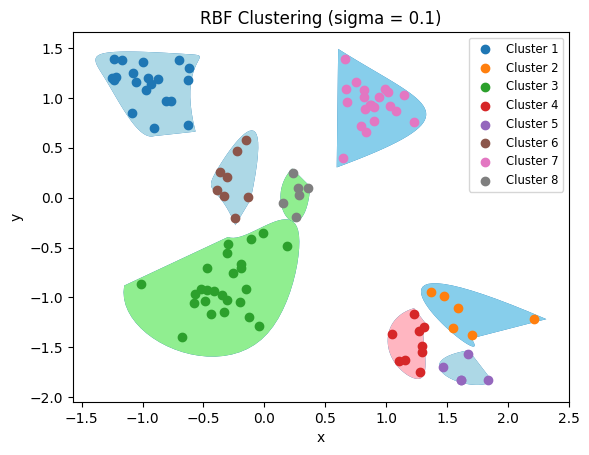
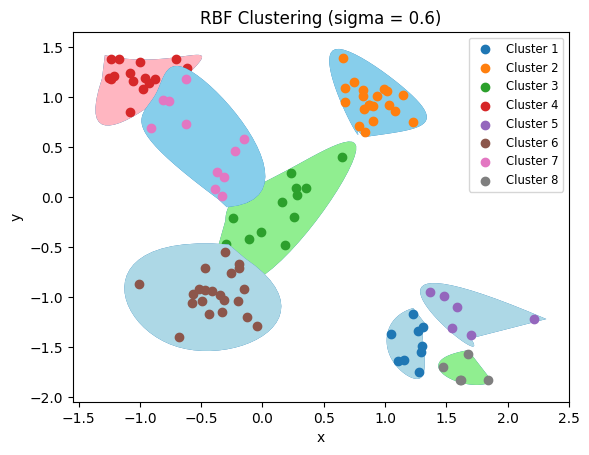
当\(\sigma = 0.5\)时，

\(\sigma = 1, 0.1, 0.01\)时，借鉴博客的分类结果

• 图片来自https://blog.csdn.net/weixin_44492824/article/details/122546701

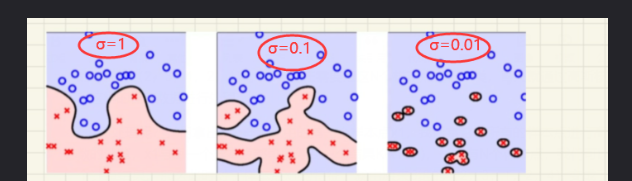
\(\quad \quad\) 由上图可以发现\(\sigma\)越小， 对数据划分越细致，也越容易倒置过拟合，由借鉴博客的理解可知：

\(\sigma\)越小， 对于每一对样本点之间得出的高斯核函数值就越大，也就是把各个样本之间的距离算的越远了，那么模型就越偏向于把这些不同的样本点归为不同的类；如果\(\sigma\)很大，则算出来样本点之间的距离就很近，模型会偏向于把这些归为同一类。

拉普拉斯矩阵

\(\quad \quad\)拉普拉斯矩阵\(L = D - W\)， \(D\)即为度矩阵，它是一个对角阵，而\(W\)即为邻接矩阵。

\(\quad \quad\)拉普拉斯矩阵有一些很好的性质：

1. 拉普拉斯矩阵是对称矩阵，可以由\(D\)和\(W\)都是对称矩阵而得。

2. 由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数。

3. 对于任意的向量\(f\),有

   \[f^TLf = \dfrac{1}{2}\sum\limits_{i,j =1}^{n}w_{ij}(f_i - f_j)^2 \]

这个公式可由拉普拉斯矩阵的定义获得：

\[f^TLf = f^TDf - f^TWf = \sum\limits_{i = 1}^{n}d_if_i^2-\sum\limits_{i, j=1}^{n}w_{ij}f_if_j \\ = \dfrac{1}{2}(\sum\limits_{i = 1}^{n}d_if_i^2 - 2\sum\limits_{i,j=1}^{n}w_{ij}f_if_j + \sum\limits_{j = 1}^{n}d_jf_j^2) = \dfrac{1}{2}\sum\limits_{i, j=1}^{n}w_{ij}(f_i - f_j)^2 \]

4. 拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0，即 0 = \(\lambda_1 \leq\lambda_2 \leq \ldots \leq \lambda_n\), 且最小的特征值为0。

回归线代课本：

\(\quad \quad\)设二次型\(f(x) = x ^TAx\),

• 如果对于任何\(x \neq 0\), 都有是\(f(x) > 0\)（显然\(f(0)= 0\)), 则称\(f\)为正定二次型，并称对称矩阵\(A\)是正定的；
• 如果对任何\(x\neq 0\)都有\(f(x) < 0\), 则称\(f\)为负定二次型， 并称对称矩阵\(A\)是负定的。

无向图切图

\(\quad \quad\) 对于无向图\(G\)的切图， 我们的目标是将图\(G(V,E)\)切成互相没有连接的\(k\)个子图，每个子图点的集合为：\(A_1, A_2, \ldots A_k\), 它们满足\(A_i \cap A_j = \varnothing,\)且\(A_1\cup A_2 \cup\ldots\cup A_k = V\) 。

\(\quad \quad\) 对于任意两个子图点的集合\(A,B \subset V, A\cap B= \varnothing\), 定义\(A\)和\(B\)之间的切图权重为：

\[W(A, B) = \sum\limits_{i\in A, j \in B} w_{ij} \]

\(\quad \quad\)那么对于k个子图点的集合:\(A_1, A_2, \cdots A_k\)，定义切图cut为：

\[cut(A_1, A_2, \ldots A_k) = \dfrac{1}{2}\sum\limits_{i = 1}^{k}W(A_i, \bar{A_j}) \]

\(\quad \quad\)其中\(\bar{A}_i\)为\(A_i\)的 补集，意为除\(A_i\)子集外其他\(V\)的子集的并集。

\(\quad \quad\)那么如何切图可以让子图内的点权重和高，子图间的点权重值和低那？一个自然的想法就是最小化\(cut(A_1, A_2, \cdots A_k)\)，但是可以发现，这种极小化的切图存在问题，如下图：

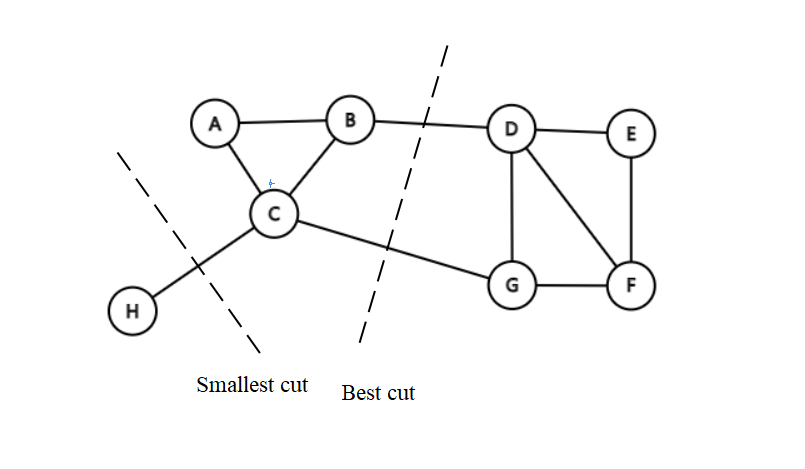
\(\quad \quad\)选择一个权重最小的边缘的点，比如\(C\)和\(H\)之间进行cut， 这样可以最小化\(cut(A_1, A_2, \cdots A_k)\),但是却不是最优的切图，如何避免这种切图，并且找到类似图中"Best Cut"这样的最优切图，就是目前谱聚类使用的切图方法。

2. 谱聚类之切图聚类

\(\quad \quad\)为了避免最小切图导致的切图效果不佳，需要对每个子图的规模作出限定，一般来说，有两种切图方式，第一种是\(RatioCut\), 第二种是\(Nust\)。

\(RatioCut\) 切图

\(RatioCut\)切图为了避免以上出现的最小切图问题， 因此对于每个切图，不光考虑最小化\(cut(A_1, A_2, \ldots A_k)\),它还同时考虑最大化每个子图点的个数，即：

\[RatioCut(A_1, A_2,\ldots A_k) = \dfrac{1}{2} \sum\limits_{i = 1}^{k} \dfrac{W(A_i, \bar{A})}{\mid A_i \mid} \]

\(\quad \quad\) 那么怎么最小化\(RatioCut\)函数呢？，巨人们发现\(RatioCut\)函数可以通过如下方式获得，

\(\quad \quad\)我们引入指示变量\(h_j \in \{ h_1, h_2 \ldots h_k\}, j = 1, 2, \ldots k\),对于任意一个向量\(h_j\), 它是一个n维向量(n为样本数), 我们定义\(h_{ij}\)为：

\[h_{ij} = \begin{cases} 0 & v_i\notin A_j\\ \dfrac{1}{\sqrt{\mid A_i \mid}} & v_i \in A_j \end{cases} \]

\(\quad \quad\)那么对于\(h_i^TLh_i\)，有：

\[\begin{align} h_i^TLh_i &= \dfrac{1}{2}\sum_{m = 1}\sum_{n =1} w_{mn}(h_{im} - h_{in})^2 \notag \\ &=\dfrac{1}{2}(\sum\limits_{m \in A_i, n\notin A_i}w_{mn}(\dfrac{1}{\sqrt{\mid A_i \mid}} - 0)^2 + \sum\limits_{m \notin A_i, n\in A_i}w_{mn}(0 - \dfrac{1}{ \sqrt{\mid A_i \mid}})^2) \notag \\ &=\dfrac{1}{2}(\sum\limits_{m \in A_i, n\notin A_i}w_{mn}\dfrac{1}{{\mid A_i \mid}} + \sum\limits_{m \notin A_i, n\in A_i}w_{mn}\dfrac{1}{ {\mid A_i \mid}}) \notag \\ &= \dfrac{1}{2}(cut(A_i, \bar{A_i} )\dfrac{1}{\mid A_i\mid} + cut(\bar{A_i}, A_i)\dfrac{1}{\mid A_i\mid}) \notag \\ &= \dfrac{cut(A_i, \bar{A_i})}{\mid A_i \mid} \end{align} \]

\(\quad \quad\) 上式的推导里利用了上文提及的拉普拉斯矩阵的性质3，第二行的推导利用了指示向量的定义，由以上公式可以看出，对于某一个子图\(i\), 它的\(RatioCut\)对应于\(h_i^TLh_i\),那对于k个子图，对应的\(RatioCut\)函数表达式为：

\[RatioCut(A_1, A_2, \ldots A_k) = \sum\limits_{i = 1}^{k} h_i^TLh_i = \sum\limits_{i = 1}^{k} (H^TLH)_{ii} = tr(H^TLH) \]

\(\quad \quad\)上式推导利用了指示变量，其中\(tr(H^TLH)\)为矩阵的迹。也就是说，\(RatioCut\)切图，实际上就是最小化\(tr(H^TLH)\)。注意到\(H^TH = I\), 这个式子成立是因为不同\(A\)的点集的节点都是不同的， 则切图优化目标为：

\[\underbrace{\arg \min}_H ~tr(H^TLH) ~s.t.~H^TH = I \]

\(\quad \quad\)注意\(H\)矩阵里面的每一个指示变量都是\(n\)维的， 向量中每个变量的取值为0或者\(\dfrac{1}{\sqrt{\mid A_i \mid}}\),就有\(2^n\)种取值，优化目标的H是一个NP难的问题，如何解决，注意观察\(tr(H^TLH)\)中每一个优化子目标\(h_i^TLh_i\)，其中\(h\)是正交基（\(\sum \limits _{i = 1} ^{n}h_i = 1\)）, \(L\)为对称矩阵，这里的\(h_i^TLh_i\)就是一个正定二次型。

正定二次型：

\[\textbf{[} \begin{array}{cccc} x_1& x_2&\cdots& x_n \end{array} \textbf{]} \left[ \begin{array}{ccc} a_{11}&a_{12} & \cdots & a_{1n}\\ a_{21}&a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \ddots\\ a_{n1}&a_{n2} & \cdots & a_{nn}\\ \end{array} \right] \left[ \begin{array}{cccc} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right] \\ = f(x)= a_{11}x^2 + a_{22}x^2 + \cdots + a_{nn}x^2 + 2 a_{12}x_1x_2 +\cdots + 2a_{nn -1}a_{n-1n}x_nx_{n - 1} \]

PCA原理和这里求最优解原理同理，借鉴网站：https://zhuanlan.zhihu.com/p/84946694

\(\quad \quad\)此时\(h_i^TLh_i\)的最大值为\(L\)的最大特征值，最小值是\(L\)的最小特征值， 主成分分析PCA中目标是求解协方差矩阵的（对应此处的拉普拉斯矩阵\(L\))的最大的特征值，而在谱聚类中， 目标是找到使得目标函数最小的特征值，得到对应的特征向量，此时对应二分切图效果最佳。

\(\quad \quad\) 对于\(h_i^TLh_i\)，我们的目标是找到最小的\(L\)的特征值，而对于\(tr(H^TLH)= \sum\limits_{i = 1}^{k}h_i^TLh_i\)， 则目标就是找到k个最小的特征值，一般来说，k远远小于n，也就是说，此时进行了维度规约，将维度从n降到了k,从而近似可以解决这个NP难的问题。

\(\quad \quad\)通过找到\(L\)的最小的k个特征值，可以得到对应的k个特征向量，这k个特征向量组成一个$ n\times k\(维度的矩阵，即为我们的\)H\(， 一般需要对\)H$矩阵按行做标准化， 即

\[h_{ij}^* = \dfrac{h_{ij}}{(\sum\limits_{t = 1}^{k} h_{it}^2) ^{\frac{1}{2}}} \]

\(\quad \quad\)由于在使用维度规约的时候损失了少量信息，导致得到的优化有的指示向量h对应的H现在不能完全指示各样本的归属，因此一般在得到\(n\times k\)维度的矩阵H后还需要对每一行进行一次传统的聚类，比如使用K-means聚类。

\(Ncut\)切图

\(\quad \quad\)\(Ncut\)切图和\(RatioCut\)切图很类似，但是把\(RatioCut\)的分母\(\mid A_i \mid\)换成\(vol(A_i)\)，由于子图样本的个数多并不一定权重就大，切图时基于权重更符合目标，因此一般来说\(Ncut\)切图优于\(RatioCut\)切图。

\[Ncut(A_1, A_2,\ldots,A_k) = \dfrac{1}{2}\sum\limits_{i = 1}^{k}\dfrac{W(A_i, \bar{A_i})}{vol(A_i)} \]

\(\quad \quad\) 对应的，\(Ncut\)切图对指示向量\(h\)做了改进，注意到\(RatioCut\)切图的指示向量使用的是\(\dfrac{1}{\sqrt{\mid A_i \mid}}\)标识样本归属，而\(Ncut\)切图使用了子图权重\(\dfrac{1}{\sqrt{vol(A_j)}}\)来标识指示向量h,定义如下：

\[h_{ij} = \begin{cases} 0 & v_i\notin A_j\\ \dfrac{1}{\sqrt{vol(A_j)}}& v_i\in A_j \end{cases} \]

\(\quad \quad\)同理，对于\(h_i^TLh_i\)有：

\[\begin{align} h_i^TLh_i &= \dfrac{1}{2}\sum_{m = 1}\sum_{n =1} w_{mn}(h_{im} - h_{in})^2 \notag \\ &=\dfrac{1}{2}(\sum\limits_{m \in A_i, n\notin A_i}w_{mn}(\dfrac{1}{\sqrt{ vol(A_i) }} - 0)^2 + \sum\limits_{m \notin A_i, n\in A_i}w_{mn}(0 - \dfrac{1}{ \sqrt{ vol(A_i) }})^2) \notag \\ &=\dfrac{1}{2}(\sum\limits_{m \in A_i, n\notin A_i}w_{mn}\dfrac{1}{{vol( A_i)}} + \sum\limits_{m \notin A_i, n\in A_i}w_{mn}\dfrac{1}{ {vol( A_i) }}) \notag \\ &= \dfrac{1}{2}(cut(A_i, \bar{A_i} )\dfrac{1}{ vol(A_i)} + cut(\bar{A_i}, A_i)\dfrac{1}{vol(A_i)}) \notag \\ &= \dfrac{cut(A_i, \bar{A_i})}{vol( A_i) } \end{align} \]

\(\quad \quad\) 推导方式和\(RatioCut\)完全一致，也就是说，我们的优化目标仍然是：

\[Ncust(A_1,A_2,\ldots ,A_k)=\sum\limits_{i = 1}^{k}h_i^TLh_i = \sum\limits_{i = 1}^{k}(H^TLH)_{ii}= tr(H^TLH) \]

\(\quad \quad\) 但是此时的\(H^TH\neq I\),而是\(H^TDH=I\)。推导如下：

\[h_iDh_i=\sum\limits_{j = 1}^{n}h_{ij}^2d_j=\dfrac{1}{vol(A_i)}\sum\limits_{j\in A_i}d_j = \dfrac{1}{vol(A_i)}vol(A_i) = 1 \]

\(\quad \quad\) 也就是说，我们的优化目标最终为：

\[\underbrace{\arg \min}_H ~tr(H^TLH) ~s.t.~H^TDH = I \]

\(\quad \quad\)此时的H中的指示变量\(h\)并不是标准正交基，所以在\(RatioCut\)中的降维思想不能直接用，那就间接变换一下。

\(\quad \quad\)令\(H= D^{-\frac{1}{2}}F\)，则：\(H^TLH = F^TD^{-\frac{1}{2}}LD^{-\frac{1}{2}}F, H^TDH = F^TF = I\),也就是优化目标变成了:

\[\underbrace{\arg \min}tr(F^TD^{-\frac{1}{2}}LD^{-\frac{1}{2}}F) ~s.t.~F^TF = I \]

\(\quad \quad\)可以发现这个式子和\(RatioCut\)基本一致，只是中间的\(L\)变成了\(D^{-\frac{1}{2}}L D^{-\frac{1}{2}}\)。接着就可以按照\(RatioCut\)的思想，求出\(D^{-\frac{1}{2}}L D^{-\frac{1}{2}}\)的最小的前k个特征值，然后求出对应的特征向量，并标准化，得到最后的的特征矩阵\(F\),最后对\(F\)进行一次传统的聚类(比如K-Means)即可。

\(\quad \quad\)一般来说， \(D^{-\frac{1}{2}}L D^{-\frac{1}{2}}\)相当于对拉普拉斯俊泽和你\(L\)做了一次标准化，即\(\dfrac{L_{ij}}{\sqrt {d_i\times d_j}}\)。

3. 谱聚类算法流程

\(\quad \quad\)一般来说，谱聚类主要的注意点在相似矩阵的生成方式，切图的方式以及最后的聚类方法等方面上。

\(\quad\quad\)最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是\(Ncut\)，而到最后常用的聚类方法是\(K-Means\)。下面以\(Ncut\)总结谱聚类算法流程。

\(\quad\quad\)输入：样本集\(D = (x_1, x_2, \dots, x_n)\),相似矩阵的生成方式，降维后的维度\(k_1\)聚类方法，聚类后的维度\(k_2\)

\(\quad \quad\)输出：簇划分\(C(c_1,c_2, \ldots,c_{k_2})\)

\(\quad \quad\) 1）根据输入的相似矩阵的生成方式构建样本的相似矩阵\(S\)

\(\quad \quad\) 2）根据相似矩阵S构建邻接矩阵\(W\)， 构建度矩阵\(D\)

\(\quad \quad\) 3）计算拉普拉斯矩阵\(L\)

\(\quad \quad\) 4）构建标准化后的拉普拉斯矩阵\(D^{-\frac{1}{2}}L D^{-\frac{1}{2}}\)

\(\quad \quad\) 5）计算\(D^{-\frac{1}{2}}L D^{-\frac{1}{2}}\)最小的\(k_1\)个特征值所各自对应的特征向量\(f\)

\(\quad \quad\) 6）将各自对应的特征向量\(f\)组成的矩阵按行标准化，最终组成\(n \times k_1\)维的特征矩阵\(F\)

\(\quad \quad\) 7）将\(F\)中的每一行作为一个\(k_1\)维的样本，共\(n\)个样本，用输入的聚类方法进行聚类，聚类维度为\(k_2\)

\(\quad \quad\) 8）得到簇划分\(C(c_1, c_2, \ldots ,c_{k_2})\)

4. 谱聚类算法总结

谱聚类算法的优点：

• 谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效，这点传统聚类算法比如K-Means很难做到。
• 由于使用了降维，因此在处理高维聚类时的复杂度比传统聚类算法好。

谱聚类算法的缺点：

• 如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。
• 聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。