2023寒假训练收官赛部分题题解
2023寒假训练收官赛(部分题总结)
赛时过题
L1-1 这是一个签道题
题目描述
转眼间, 寒假就快结束了, 寒假训练营也接近尾声, 可学长小P却感觉什么都没学到, 还是一如既往的菜, 你能帮他问问时间都去哪儿了吗?
输入格式:
无输入数据
输出格式:
输出一行"shi jian dou qu na er le ?", 行末不要有多余空格。
输入样例:
输出样例:
shi jian dou qu na er le ?
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
cout << "shi jian dou qu na er le ?" << "\n";
return 0;
}
L1-2 creeper?
题目描述
近期小P学长迷上了mc这款老游戏, 众所周知, mc有一首名为《reveng**e》的曲子, 这个曲子好听的同时也常用来整活接力, 现在小P学长已经出了上句, 请你接出下句, 下面歌词即为输入数据范围, 若为最后一句则输出"ohohohohohohohoh!"。

Creeper?
Awwwwwww man?
So we back in the mine
Got our pickaxe swinging from side to side
Side-side to side
Thistask, a gruelingone
Hope to find some diamonds tonight,night, night
Diamonds tonight
Heads up
You hear a sound, turn around and look up
Total shock fills your body
Oh, no, it's you again
I can never forget those eyes, eyes, eyes
Eyes-eye-eyes
输入格式:
如题所示
输出格式:
输入一行字符串为上句的下句, 行末不要有多余空格或者换行。
输入样例:
Creeper?
输出样例:
Awwwwwww man?
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s[14] = {"Creeper?","Awwwwwww man?","So we back in the mine","Got our pickaxe swinging from side to side","Side-side to side","Thistask, a gruelingone","Hope to find some diamonds tonight,night, night","Diamonds tonight","Heads up","You hear a sound, turn around and look up","Total shock fills your body","Oh, no, it's you again","I can never forget those eyes, eyes, eyes","Eyes-eye-eyes"};
string ans;
getline(cin,ans);
for(int i = 0; i < 14; i++)
{
if(s[i] == ans && i != 13)
{
cout << s[i+1];
return 0;
}
if(i == 13 && s[i] == ans)
{
cout << "ohohohohohohohoh!";
return 0;
}
}
return 0;
}
L1-3 小蒲和音游
题目描述
phigros是一款国产音游,对于一首歌曲,有不同的音符需要你去打击。

根据你打击音符的准确度,可以分为如下几个判定perfect,good,bad,miss,获得的分数分别为这个音符的分数的100%,65%,0%,0%,每一个音符分数相同,在课题模式下,本首歌最后得到的分数计算公式根据本首歌所打出的perfect,good,bad,miss个数,按照如下方式计算
(perfect音符个数∗100%+good音符个数∗65%)∗单个音符分数
根据最后不同的总得分,你将获得如下的评级:
| 得分 | 评级 |
|---|---|
| 1000000 | phi |
| 960000-999999 | V |
| 920000-959999 | S |
| 880000-919999 | A |
| 820000-879999 | B |
| 700000-819999 | C |
| 0-699999 | F |
现在小蒲在课题模式下打某歌每一个音符的分数为1000,那么音符个数也是1000,现在给出他的perfect,good,ba**d,mi**ss的音符个数,请你给出他的评级。
输入格式:
一行四个数,如题意所示。
输出格式:
输出一行,代表打歌评级。
输入样例1:
1000 0 0 0
输出样例1:
phi
输入样例2:
999 1 0 0
输出样例2:
V
数据范围及约定
每一个音符的分数为1000,这四个数之和保证为1000。
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
提交代码
-
比较快的写法从小到大判断
-
if(ans >= 0) { if(ans <= 699999) puts("F"); else if(ans <= 819999) puts("C"); else if(ans <= 879999) puts("B"); else if(ans <= 919999) puts("A"); else if(ans <= 959999) puts("S"); else if(ans <= 999999) puts("V"); else puts("phi"); }
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int a,b,c,d;
cin >> a >> b >> c >> d;
int ans = a *1000 + 650 * b;
if(ans == 1000000) puts("phi");
else if(960000 <= ans && ans <= 999999) puts("V");
else if(920000 <= ans && ans <= 959999) puts("S");
else if(880000 <= ans && ans <= 919999) puts("A");
else if(820000 <= ans && ans <= 879999) puts("B");
else if(700000 <= ans && ans <= 819999) puts("C");
else if(0 <= ans && ans <= 699999) puts("F");
return 0;
}
L1-4 小P的圆锥曲线!
题目描述
圆锥曲线问题在高中算的上数一数二的几何难题,即便升上了大学,小P同学还是忘不了被圆锥曲线折磨的恐惧,现在给出a,b,c,请你判断 \(ax^2 + bx^2 =c\)是什么图形。
若为圆, 则输出"Circle", 若为椭圆, 则输出"Ellipse",若为双曲线,则输出"Hyperbola", 否则输出"nothing"。
注: 点不算作任何图形。
形如的\(x^2 +y^2=r^2\)为圆,
形如的\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)为椭圆,
形如\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\quad or \quad \dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\)的为双曲线。
输入格式:
输入在一行中给出三个数a(−10≤a≤10),b(−10≤b≤10),c(−10≤c≤10)。
输出格式:
输出一行为方程表示图形(行末无多余换行或空格)。
输入样例:
2 1 1
输出样例:
在这里给出相应的输出。例如:
Ellipse
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int a,b,c;
cin >> a >> b >> c;
if(a==b && a > 0 && c > 0) puts("Circle");
else if(a==b && a < 0 && c < 0) puts("Circle");
else if(a != b && a > 0 && b > 0 && c > 0) puts("Ellipse");
else if(a != b && a < 0 && b < 0 && c < 0) puts("Ellipse");
else if(a > 0 && b < 0 && c) puts("Hyperbola");
else if(a < 0 && b > 0 && c) puts("Hyperbola");
else puts("nothing");
return 0;
}
L1-5 小P的字符串模拟(easy)
题目描述
小P是一位蒟蒻acmer,为了提升技术,决定在寒假猛刷题,最近, 小P发现了一道极好的字符串题目,来自于寒假训练营,题目大意如下:
lscjj被鉴定成毒瘤出题人。
一个长度为n且仅有小写字母的字符串s,lscjj的毒瘤程度为s串的"udu"子序列的个数。
现在lscjj痛心疾首,想降低毒瘤程度。
lscjj想修改其中s串的一个字符(也可以不修改。只能修改成小写字母),需要修改后毒瘤程度最小。
子序列:指按照原串的顺序取一些字符,组成新的字符串。例如"dudu"、"udu"是"dudovoudu"的子序列,而"uudd"、"abc"不是。
lscjj想知道修改后的s是什么?
小P同学想进一步减少这题的毒瘤程度,他决定把原题的子序列换成子字符串。
子字符串:指按照原串的顺序取段字符串。例如"dudo"、"udo"是"dudovoudu"的子字符串,而"dudv"、"oou"不是。
小P想知道原题改为子字符串后, 根据题意修改毒瘤程度, 修改后的毒瘤程度是多少?
输入格式:
输入第一行n(1≤n≤2×\(10^5\)), 为字符串的长度。
接下来一行, 输入一个仅包含小写字母的字符串s。
输出格式:
输出一行数字为s的毒瘤程度。
输入样例:
在这里给出一组输入。例如:
9
duduvoudu
输出样例:
在这里给出相应的输出。例如:
1
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int ans = 0;
int n;
cin >> n;
string s;
cin >> s;
int flag = 0;
int late = -1;
for(int i = 0; i < n-2; i++)
{
if(s[i]=='u' && s[i+1] == 'd' && s[i+2] == 'u')
{
ans++;
if(late == i) flag = 1;
// cout << late << " "<< i <<"\n";
late = i + 2;
}
}
// cout << flag << "\n";
if(flag) ans--;
if(ans) ans--;
cout << ans << "\n";
return 0;
}
L1-6 公平博弈
题目描述
请见下面赛后补题
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t--)
{
long long n;
cin >> n;
if(n < 3) puts("Bob");
else puts("Alice");
long long k = 1;
int flag =0;
for(int i = 0; i < 64; i++)
{
if(k > n) break;
if(k == n) flag = 1;
k *= 2;
}
if(flag) puts("Bob");
else puts("Alice");
}
return 0;
}
赛后补题
L1-6 公平博弈
题目描述
给定一个长为n,宽为1的矩形,可以对矩形进行如下操作:
1、沿某一行切开,将矩形分为上下两部分。
2、沿某一列切开,将矩形分为左右两部分。
特别的,需要保证切开后的两部分的长和宽都为整数且他们的面积不相等。
现在Alice Bob开始交替对矩形进行操作,两人都足够聪明。
Alice先手进行操作,问在添加以下规则以后谁会赢(一方不能继续操作即为输)。
规则一、每次切开后抛弃掉面积更大的一部分留下面积小的一部分继续操作。
规则二、每次切开后抛弃掉面积更小的一部分留下面积大的一部分继续操作。
注:在添加新的规则后依旧只能进行沿行切开合沿列切开两种操作,且规则一实行期间规则二不实行,规则二实行期间规则一不实行。
输入格式:
输入第一行包含一个正整数t,表示样例个数(1≤t≤\(10^5\))。
接下来t行每行包含一个正整数n(1≤n≤\(10^8\))。
输出格式:
每个样例输出包含两行,第一行为添加规则一后谁会赢,第二行为添加规则二后谁会赢。
如果Alice将会获胜则输出"Alice"(不包含引号),否则输出"Bob"(不包含引号)。
输入样例:
在这里给出一组输入。例如:
2
4
3
输出样例:
在这里给出相应的输出。例如:
Alice
Bob
Alice
Alice
代码长度限制 16 KB 时间限制 500 ms 内存限制
思路点拨
-
积累知识点:判断是否1,2,4,8,16这种2的n次方数的技巧,也就是二进制只有第一位为1,其余为0。
-
(n & -n) == n -
注意
(n & -n)是为了得到最后一位1组成的数。 -
还有一种函数的方法,
__builtin_popcountll(n) == 1 -
__builtin_popcountll(n)或者__builtin_popcountl(n)作用就是判断n二进制数会有几个1,只有二的次方二进制位只有一个1。 -
策略1就简单思考一下就好了,n<3 时先手必输,其余先手必赢,考虑n>=3时,都会分为1和n-1,先手必胜。
-
策略2博弈判断思路如下:
-
熟练利用博弈论sg函数进行打表
-
对于策略2打表结果,打表什么时候Alice(先手)会输,也可以自己去推,前提条件一定是双方足够聪明
1 2 4 8 16 32 64 128 256 512
- 打表代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1000;
int sg[N];
int main()
{
for(int i = 1; i < N; i++)
{
set<int> vals;
for(int j = i / 2 + 1; j < i; j++)
{
vals.insert(sg[j]);
}
while(vals.count(sg[i]))
{
sg[i]++;
}
}
for(int i = 1; i < N; i++)
{
if(!sg[i]) cout << i << " ";
}
return 0;
}
借鉴代码
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve()
{
i64 n;
cin >> n;
if(n == 1 || n == 2)
{
cout << "Bob\n";
}
else
{
cout << "Alice\n";
}
if((n & -n) == n)
{
cout << "Bob\n";
}
else
{
cout << "Alice\n";
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t--)
{
solve();
}
return 0;
}
L2-1 树状数组
题目描述
lscjj最近学会了树状数组,树状数组是利用二进制表示区间的方法高效拼接出任意长度的数组前缀和的算法。
具体来讲,树状数组定义了一个叫做lowbit的函数lowbit(x)表示二进制表示x时,x的最低二进制位表示的数值。例如lowbit(10)=2,lowbit(7)=1等。
在树状数组上,第i个元素储存了从第i−lowbit(i)+1个元素到第i个元素的区间和,这个区间的大小恰好为lowbit(i)。
lscjj发现,可以将树状数组中的第i个元素对应二叉树上编号为i的节点构造出一棵二叉树。现在有一个尺寸大小为N=2k的树状数组,lscjj按照如下的规则构造出一个“树状数组二叉树”。
- 编号为i的节点的深度为log2(lowbit(N))−log2(lowbit(i))。
- 整棵二叉树的中序遍历节点编号顺序为1,2,3...N−1,N。
如果你不理解这个“树状数组二叉树”构造的限制条件的话,这里有一个生动形象的例子。
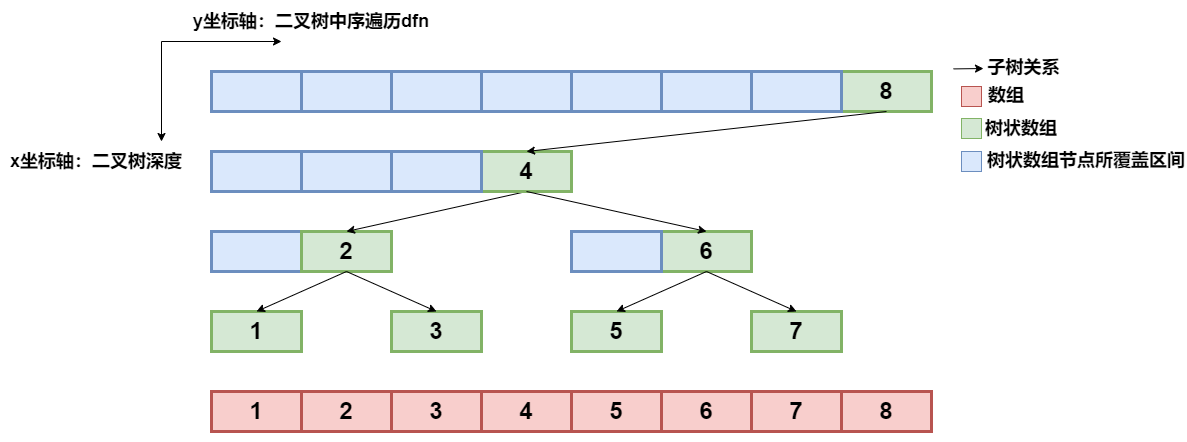
如图所示,我们以左上角为坐标原点,向下为x轴正方向,向右为y轴正方向建立直角坐标系。
限制条件1中,节点深度的几何意义实际上就是二叉树的节点在图像中的x轴坐标。
限制条件2中,中序遍历节点编号顺序的几何意义实际上就是二叉树的节点在图像中的y轴坐标。
除了本题以外,实际上按照标准在绘制任何一棵二叉树时都可以遵循这个规则确定二叉树的节点在图像中的横纵坐标。
现在lscjj想知道对于树状数组生成的二叉树上编号为x的节点他的p级祖先的节点编号。
注:
1、题目背景摘抄自牛客寒假训练营,因为zngg写得太好了很全面所以直接偷。
2、树上一个点的p级祖先即从当前点向父节点方向移动p步后到达的节点,如在上图中1的一级祖2,1的二级祖先为4。
输入格式:
输入第一行包含两个整数k(0≤k≤30),q(1≤q≤\(10^5\))。表示树状数组的尺寸N=\(2^k\),查询的次
数为q。
接下来q行每行两个整数x(1≤x≤N),p(0≤p≤k)表示查询节点的编号和需要查询的祖先级数。
输出格式:
输出包含q行,每行包含一个整数y表示y是x的p级祖先,特别的,如果y>N则输出"−1"(不包含引号)。
输入样例:
在这里给出一组输入。例如:
3 2
1 1
5 2
输出样例:
在这里给出相应的输出。例如:
2
4
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
思路点拨
- 首先可以发现一个性质,对于如上图,一个数的位置的层数,从低向上开始算起,和该数的二进制最后一个1从右往左的位置相同
- eg, 2二进制为10,则位于第二层,6二进制为110,则位于第二层,4,二进制为100,则位于第三层。
- 所以控制最后一位1的位置非常重要,你会发现对于6(二进制110)上一级应该为100,只要改变最后一位1的位置即可,这里对应情况是最后一位1的前一位为1,如果想转移到100,必须要先减去10代表的2,即减去最后一位1构成的数。
- 对于另一种情况,2的二进制为10,它的上一级为100,也就是说需要左移一位,这里对应情况是最后一位1的前一位为0,如果想要转移到100,必须要加上10,即加上最后一位1构成的数。
- 以上两种情况对任何数都适用,eg 9(1001),11(1011) , 9由于最后一位1前一位是0,所以需要将1001 加上最后一位1构成的数1 为1010,而11 由于最后一位1前一位是1,所以需要将1001 减去最后一位1构成的二进制数 1 为1010。
借鉴代码
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve()
{
int k, q;
cin >> k >> q;
while(q--)
{
i64 x;
int p;
cin >> x >> p;
int lv = -1;
for(int i = 30; i >= 0; i--)
{
if(x >> i &i)
{
lv = i;
}
}
for(int i = 0; i < p; i++)
{
if(x >> (lv + 1) & 1)
{
x -= (1ll << lv);
}
else
{
x += (1ll << lv);
}
lv++;
if(x > (1ll << k))
{
x = -1;
break;
}
}
cout << x << "\n";
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t--)
{
solve();
}
return 0;
}
L2-2 沙盘游戏
题目描述
沙盒游戏(Sandbox Games),是由沙盘游戏演变而来,自成一种游戏类型,由一个或多个地图区域构成,往往包含多种游戏要素,包括角色扮演,动作、射击、驾驶等等。
小a所在公司开发了一种沙盒游戏,这款游戏上线之后由于其精美的画风和强大的制造系统受到玩家一致好评。其中该游戏的一个特色功能就是玩家可以自己自由创造一张地图,并在地图上分布游戏任务,审核通过即可上线。小a就是该游戏的审核员之一。审核要求除了绿色健康无不良导向之外,对于玩家上传的地图上的游戏任务也有一定要求。
我们假设一张地图上可能有n个游戏任务点,任务点之间会有相关的任务线索(即完成一个任务点后,会提示和其相关的后续任务点),每个连通的任务点的集合都有其起始任务和最终任务,玩家可以选择任意一条路径从起始任务点到最终任务点。玩家从一个任务点游玩到另一个任务点可以得到一定的愉悦值(可能为负)。
如果在游玩过程当中两次经过同一任务点,玩家就会反思,在走过的这一个“环”当中自己的愉悦值是增加了还是减少了,无疑玩家们是会讨厌后者的,因为他们会感觉自己被耍了。所以审核的最后一个要求就是保证地图中不能出现让玩家不快的负环。
现在给你一张地图上的所有游戏任务点及其之间的联结关系,请你帮小a判断一下,这张地图能不能通过审核(该地图已经满足了其他的审核要求)。如果可以请输出Win!,否则请输出Lose。
注:图中不存在重边自环,n个任务点之间不一定都连通。
输入格式:
第一行输入n(1 ≤ n ≤ 100),m(0 ≤ m ≤ n∗(n−1)/2)。其中 n 表示地图上任务点的数量(任务点序号从 1 到 n),m 表示任务点之间的联结关系的数量。
下面 m 行,每行两个正整数x, y, w(1 ≤ x,y ≤ n),由 x 到 y 存在单向联结关系,从任务点 x 游玩到任务点 y 的愉悦值为 w (−\(10^5\) ≤ w ≤ \(10^5\))。
输出格式:
如上所述。
输入样例:
5 4
1 2 -3
5 2 6
2 3 3
3 5 7
输出样例:
Win!
输入样例:
4 6
1 4 0
4 2 -2
3 4 3
1 3 10
1 2 -5
2 3 -9
输出样例:
Lose
代码长度限制 16 KB 时间限制 500 ms 内存限制 64 MB
思路点拨
- spfa判断负环即可,思路就是在利用spfa求解最短路的过程中,如果在最短路中存在负环,则一定存在最短路径上除了自己有n个点,(负环的定义是在一个环中,其环上的权值和小于0。)
提交代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> h(N,-1);
int n, m;
int w[N], ne[N], e[N], idx;
bool st[N];
int dist[N],cnt[N];
void add(int u, int v, int value)
{
e[idx] = v, w[idx] = value, ne[idx] = h[u], h[u] = idx++;
}
int spfa()
{
queue<int> q;
for(int i = 1; i <= n; i++)
{
q.push(i);
st[i] = true;
}
while(q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for(int j = h[t]; j != -1; j = ne[j])
{
int i = e[j];
if(dist[i] > dist[t] + w[j])
{
dist[i] = dist[t] + w[j];
cnt[i] = cnt [t] + 1;
if(cnt[i] >= n) return false;
if(!st[i])
{
q.push(i);
st[i] = true;
}
}
}
}
return true;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for(int i = 0; i < m; i++)
{
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
}
if(spfa()) cout << "Win!";
else cout << "Lose";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号