chap6.分支限界法

分支限界法的基本思想

以广度优先或以最小耗费（最大效益）优先的方式搜索

一个活结点最多有一次机会成为活结点（和广度优先相似，但是分支限界法去除了不可行的节点）

解空间树：

子集树

排列树

分支限界法常见的两种方式：

队列式分支限界法

优先队列式分支限界法

单源最短路径问题 O(nlogn)

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int n;
int dist[1000];
vector<int>d[1000];
int len[1000][1000];
int pre[1000];
int vis[1000];
struct cmp
{
  bool operator()(const int a,const int b)
  {
    return dist[a]>dist[b];
  }
};
void solve()
{
  priority_queue<int,vector<int>,cmp>q;
  memset(dist,0x3f3f,sizeof(dist));
  dist[1]=0;
  q.push(1);
  while(q.size())
  {
    int p=q.top();
    q.pop();
    vis[p]=1;
    for(int i=0;i<d[p].size();i++)
    {
      int u=d[p][i];
      if(vis[u])
      {
        continue;
      }
      if(dist[p]+len[p][u]<dist[u])//三角形法则，更新节点
      {
        dist[u]=dist[p]+len[p][u];
        pre[u]=p;
        q.push(u);
      }
    }
  }
}
int main()
{
  srand(time(0));
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    for(int j=i+1;j<=n;j++)
    {
      d[i].push_back(j);
      d[j].push_back(i);
      int lenn=rand()%50;
      len[i][j]=lenn;
      cout<<"i: "<<i<<" j: "<<j<<" len: "<<lenn<<endl;
      len[j][i]=lenn;
    }
  }
  solve();
  int now=n;
  cout<<"ans: "<<dist[n]<<endl;
  while(now!=1)
  {
    cout<<now<<" ";
    now=pre[now];
  }
}

装载问题 O(2^n)

队列式分支限界法

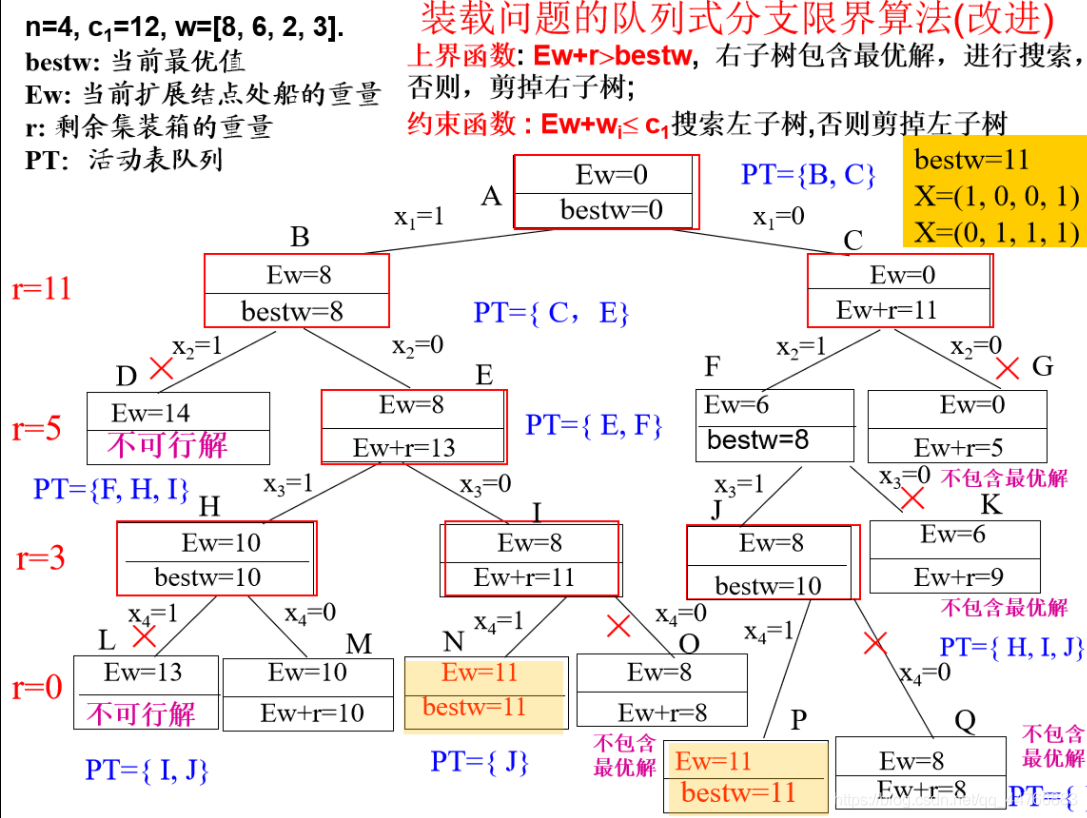
通过层序一层一层扩展，同时用限界函数（能不能不取）和约束函数（能不能取）来进行剪枝

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
struct node
{
  int id;
  node*pa;
  int w;
  node*l;
};
int n;
int w[1000];
int c1,c2;
int best;
int re;
vector<node*>ans;
void solve()
{
  int level=1;//初始层
  queue<node*>q;
  q.push(new node{0,NULL,0,NULL});//初始阶段
  while(q.size())
  {
    int len=q.size();
    for(int i=0;i<len;i++)//层序遍历
    {
      node* t=q.front();
      q.pop();
      if(level==n+1)//最后只剩叶子节点，找满足的点即可
      {
        if(t->w==best)
        {
          ans.push_back(t);
        }
        continue;
      }
      if(t->w+re-w[level]>=best)//看看剩下的全装能不能达到最优值
      {
        node*nt=new node();
        nt->id=t->id;
        nt->pa=t->pa;//同一节点顺延，相当于只记录取的点
        nt->w=t->w;
        nt->l=t->l;
        q.push(nt);
      }
      if(t->w+w[level]<=c1)//当前能否装
      {
        node*nt=new node();
        nt->id=level;
        nt->pa=t;//记录父亲节的
        nt->w=t->w+w[level];
        best=max(best,t->w+w[level]);//更新最优值
        nt->l=NULL;
        t->l=nt;
        q.push(nt);
      }
    }
    re-=w[level];
    level++;
  }
}
int main()
{
  srand(time(0));
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    w[i]=rand()%30;
    cout<<i<<" "<<w[i]<<endl;
    re+=w[i];
  }cout<<endl;
  c1=re/2+rand()%10;
  solve();
  cout<<c1<<endl;
  cout<<"ans: "<<endl;
  for(int i=0;i<ans.size();i++)
  {
    node*t=ans[i];
    while(t!=NULL)
    {
      cout<<t->id<<" ";
      t=t->pa;
    }
    cout<<endl;
  }
}

优先队列式分支限界法

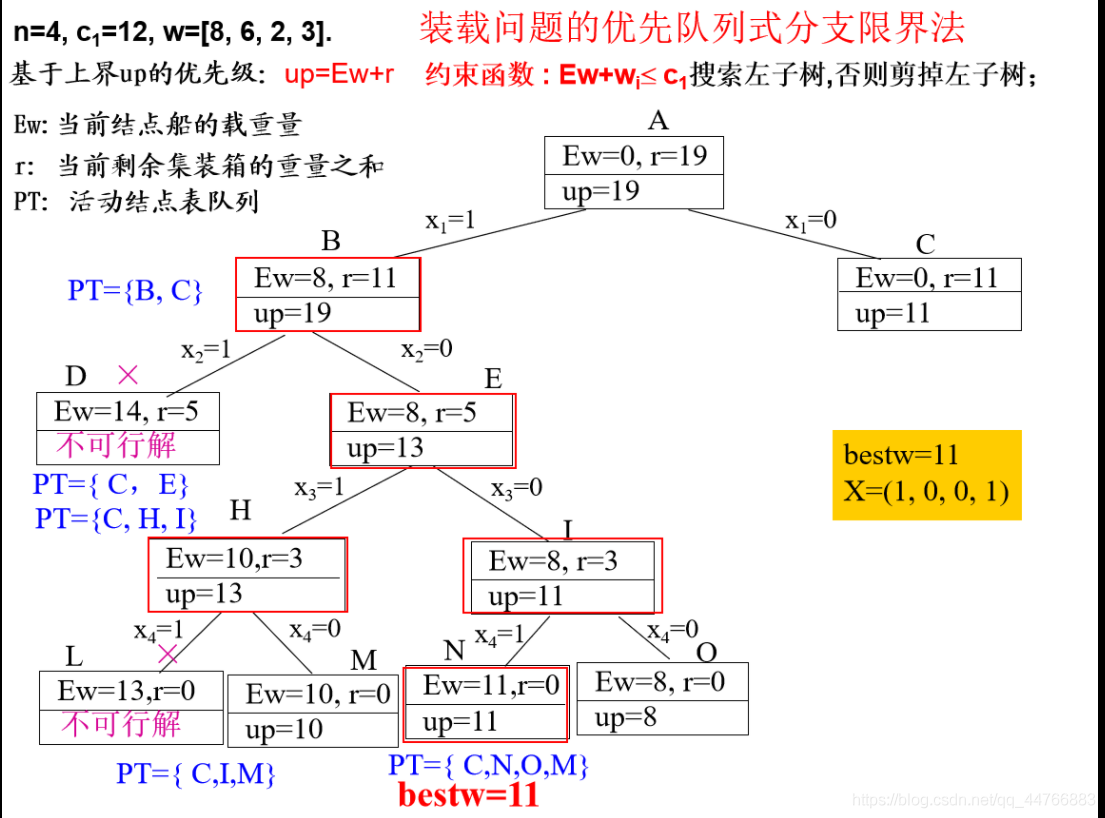
每次选出当前重量+剩余重量最大者进行扩充，找到的第一个叶子节点即为最优解

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
struct node
{
  int id;
  node*pa;
  int w;
  node*l;
  int r;//当前剩余
  int level;//下一层
};
int n;
int w[1000];
int c1,c2;
int best;
int re;
vector<node*>ans;
struct cmp
{
  bool operator()(const node*a,const node*b)
  {
    return a->w+a->r<b->w+b->r;
  }
};
void solve()
{
  priority_queue<node*,vector<node*>,cmp>q;
  q.push(new node{0,NULL,0,NULL,re,1});
  while(q.size())
  {
    node*t=q.top();
    q.pop();
    int le=t->level;
     if(le==n+1)
      {
        ans.push_back(nt);
        break;
      }
    if(t->w+w[le]<=c1)
    {
      node*nt=new node();
      nt->id=le;
      nt->pa=t;
      t->l=nt;
      nt->l=NULL;
      nt->level=le+1;
      nt->w=t->w+w[le];
      nt->r=t->r-w[le];
     
      q.push(nt);
    }
    node*nt=new node();
      nt->id=t->id;
      nt->pa=t->pa;
      nt->l=NULL;
      nt->level=le+1;
      nt->w=t->w;
      nt->r=t->r-w[le];
      q.push(nt);
  }
}
int main()
{
  srand(time(0));
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    w[i]=rand()%30;
    cout<<i<<" "<<w[i]<<endl;
    re+=w[i];
  }cout<<endl;
  c1=re/2+rand()%10;
  solve();
  cout<<c1<<endl;
  cout<<"ans: "<<endl;
  for(int i=0;i<ans.size();i++)
  {
    node*t=ans[i];
    while(t!=NULL)
    {
      cout<<t->id<<" ";
      t=t->pa;
    }
    cout<<endl;
  }
}

0-1背包

函数MaxKnapSack使用分支限界法
用子集树表示，左子节点表示当前物品放入，右子节点表示当前物品不放入。
优先级：按照优先队列中节点元素N的优先级由上界函数bound计算出的uprofit给出。（就是当前背包的重量+剩余可以放的重量）（剩余的物品按照单位重量价值非升序排序，将单位重量价值大的先放入，放不下整个物品的话，就放入一部分。）
如果到达了叶节点，由于使用的是优先队列，所有活结点价值上届不超过该叶节点价值，是最优值
左子节点：
①左儿子节点加入背包后重量小于背包总容量wt <= c；
②左子节点加入背包后判断当前背包价值是否大于总价值，如果是那么将会更新bestp，尽管当前还没有找到一个解向量
③AddLiveNode(up,cp+p[i],cw+w[i],true,i+1);
右子节点：
①当前背包价值+剩下物品装满背包的价值之和大于当前最大价值up = Bound(i+1)，up>=bestp
②up = Bound(i+1);，AddLiveNode(up,cp+p[i],cw+w[i],true,i+1);

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
struct node
{
  int id;
  node*pa;
  node*l;
  int w;
  double v;
  int level;
  double bou;
};

int n;
int c;
struct box
{
  int w;
  double v;
};
box p[1000];
double best;
double bound(int pos,double nv,int nw)//限界函数
{
  int left=c-nw;
  double val=nv;
  int i;
  if(pos==n+1)return val;
  for(i=pos;i<=n;i++)
  {
    if(p[i].w>left)break;
    left-=p[i].w;
    val+=p[i].v;
  }

  val+=(double)p[i].v/p[i].w*left;
  return val;
}
int cmp1(box a,box b)
{
  return a.v*b.w>b.v*a.w;
}
struct cmp
{
  bool operator()(const node*a,const node*b)
  {
    return (int)(10000*(a->bou))<(int)((b->bou)*10000);
  }
};
vector<node*>ans;
void solve()
{
  priority_queue<node*,vector<node*>,cmp>q;
  q.push(new node{0,NULL,NULL,0,0,1,bound(1,0,0)});
  while(q.size())
  {
    node*t=q.top();
    q.pop();
    int le=t->level;
    if(le==n+1)
    {
      ans.push_back(t);
      break;
    }
    cout<<"debug: "<<to_string(t->v+t->bou)<<"level: "<<t->level<<endl;
    if(t->w+p[le].w<=c)
    {
      node*nt=new node();
      nt->w=t->w+p[le].w;
      nt->pa=t;
      nt->l=NULL;
      nt->level=le+1;
      nt->id=le;
      nt->v=t->v+p[le].v;
      t->l=nt;
      nt->bou=t->bou;
      best=max(best,nt->v);
      q.push(nt);
    }
    if(bound(le+1,t->v,t->w)>=best)
    {
      node*nt=new node();
      nt->w=t->w;
      nt->pa=t->pa;
      nt->l=NULL;
      nt->level=le+1;
      nt->id=t->id;
      nt->v=t->v;
      nt->bou=bound(le+1,nt->v,nt->w);
      q.push(nt);
    }
    
  }
}
int main()
{
  srand(time(0));
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    p[i].w=rand()%30+1;
    p[i].v=rand()%30+1;
    c+=p[i].w;
    //cout<<i<<" w: "<<p[i].w<<" v: "<<p[i].v<<endl;
  }
  c=c-rand()%50;
  c++;
  
  best=0;
  cout<<c<<endl;
  sort(p+1,p+n+1,cmp1);
   for(int i=1;i<=n;i++)
  {
    
    cout<<i<<" w: "<<p[i].w<<" v: "<<p[i].v<<endl;
  }
  solve();
  for(int i=0;i<ans.size();i++)
  {
    node*t=ans[i];
    while(t!=NULL)
    {
      cout<<t->id<<" ";
      t=t->pa;
    }
    cout<<endl;
  }
}

旅行售货员问题

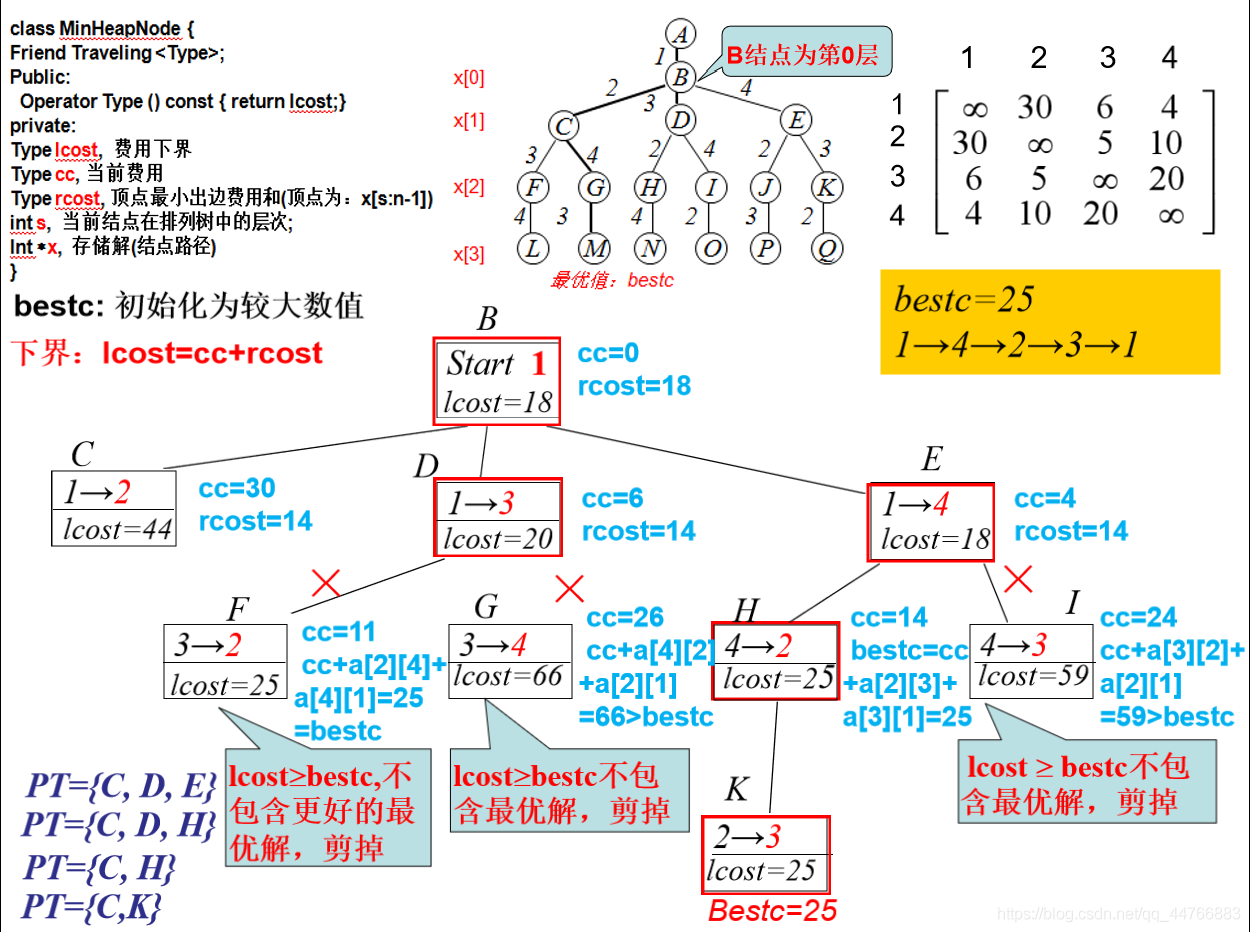
每次取lcost最小的进行查找扩展下一个点，如果下一个点的cc+rcost<best(当前最优)则表示方案可行，否则剪枝

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int n;
int minout[10000];
int len[10000][10000];
int minsum = 0;
int ans[10000];
int inf = 0x3f3f;
int sum=0;
struct node
{
  int lcost;//子树费用下界
  int cc;//当前费用
  int rcost;//x[pos:n-1]中顶点的最小出边费用和
  int pos;//当前节点路径x[0:pos]
  int x[10000];//搜索的节点集x[pos+1:n-1]
  bool operator<(const node&a)const
  {
    return lcost < a.lcost;
  }
};
void solve()
{
  minsum = 0;
  for (int i = 1; i <= n; i++)
  {
    int minn = -1;
    for (int j = 1; j <= n; j++)
    {
      if (len[i][j] != inf && (len[i][j] < minn || minn == -1)) //找i的最短出边
      {
        minn = len[i][j];
      }
    }
    if (minn == -1) //无回路
    {
      cout << "no round,error" << endl;
      return ;
    }
    minout[i] = minn;
    minsum += minn;
  }
  priority_queue<node>q;
  node t;
  for (int i = 1; i <= n; i++)
  {
    t.x[i] = i;
  }
  t.pos = 1;
  t.cc = 0;
  t.rcost = minsum;
  int best = inf;
  while (t.pos != n)
  {
    if (t.pos == n - 1)
    {
      if (len[t.x[n - 1]][t.x[n]] != inf && len[t.x[n]][t.x[1]] != inf && t.cc + len[t.x[n]][t.x[1]] + len[t.x[n - 1]][t.x[n]] < best) //存在x[n-1]:x[n]和x[n]:x[1]的边且权值更小
      {
        //更新
        best = t.cc + len[t.x[n]][t.x[1]] + len[t.x[n - 1]][t.x[n]];
        t.cc = best;
        t.lcost = best;
        t.pos++;
        q.push(t);
      }
    }
    else
    {
      for (int i = t.pos + 1; i <= n; i++)
      {
        if (len[t.x[t.pos]][t.x[i]] != inf)//存在边
        {
          int cc, rcost, lcost;
          cc = t.cc + len[t.x[t.pos]][t.x[i]];
          rcost = t.rcost - minout[t.x[t.pos]];
          lcost = cc + rcost;
          if (lcost < best)//可行
          {
            node nt;
            for (int j = 1; j <= n; j++)
            {
              nt.x[j] = t.x[j];
            }
            nt.x[t.pos + 1] = t.x[i];
            nt.x[i] = t.x[t.pos + 1];
            nt.cc = cc;
            nt.pos = t.pos + 1;
            nt.lcost = lcost;
            nt.rcost = rcost;
            q.push(nt);
          }
        }
      }

    }
    t=q.top();
    q.pop();
  }
  if (best == inf) //无回路
  {
    cout << "no round,error!" << endl;
    return ;
  }
  for (int i = 1; i <= n; i++)
  {
    ans[i]=t.x[i];
  }
  sum=best;
}
int main()
{
  srand(time(0));
  cin >> n;
  for (int i = 1; i <= n; i++)
  {
    for(int j=i+1;j<=n;j++)
    {
      int lenn=rand()%30;
      len[i][j]=lenn;
      len[j][i]=lenn;
      cout<<i<<" "<<j<<" len: "<<len[i][j]<<endl;
    }
  }
  solve();
  for(int i=1;i<=n;i++)
  {
    cout<<ans[i]<<" ";
  }
  cout<<endl;
  cout<<sum<<endl;
}

posted @ 2023-07-10 18:41 hbhhbh 阅读(72) 评论(0) 收藏举报

刷新页面返回顶部

Hbh

chap6.分支限界法

分支限界法的基本思想

解空间树：

分支限界法常见的两种方式：

单源最短路径问题 O(nlogn)

装载问题 O(2^n)

队列式分支限界法

优先队列式分支限界法

0-1背包

旅行售货员问题

公告