代数转几何：应用复数的locus

先上个匪夷所思的东西：

Fractional Linear Transformation

A fractional linear transformation is a function of the form $T(z)=\frac{(az + b)}{(cz + d)}$, where $a, b, c, d$ are complex constants and $ad-bc≠0$. These are also called Mobius transforms or bilinear transforms.

(1) Theorem: A linear fractional transformation maps lines and circles to lines and circles.

(2) Mapping of $\infty$. (the line is a considered as a circle with radius $\infty$)

(3) Composition of linear transformations are like multiplication of matrices.

(4) How to map three points on complex plane to another three points.

原理

就是每个复数可以看成复平面上的点，然后就可以固定不同的东西，比如夹角或长度或比例。

1.

如果对于一个复数$x$，如果$|x-y|$为定值，那么$y$是一个以$x$为圆心的圆。

2.

如果平面上有两个定点$A,B$，那么用$\angle ACB$就能确定由点$C$生成的两段弧。（如图，$\angle AC_1B=\angle AC_2B$，$C_1,C_2$为圆$O_1,O_2$上的点。）

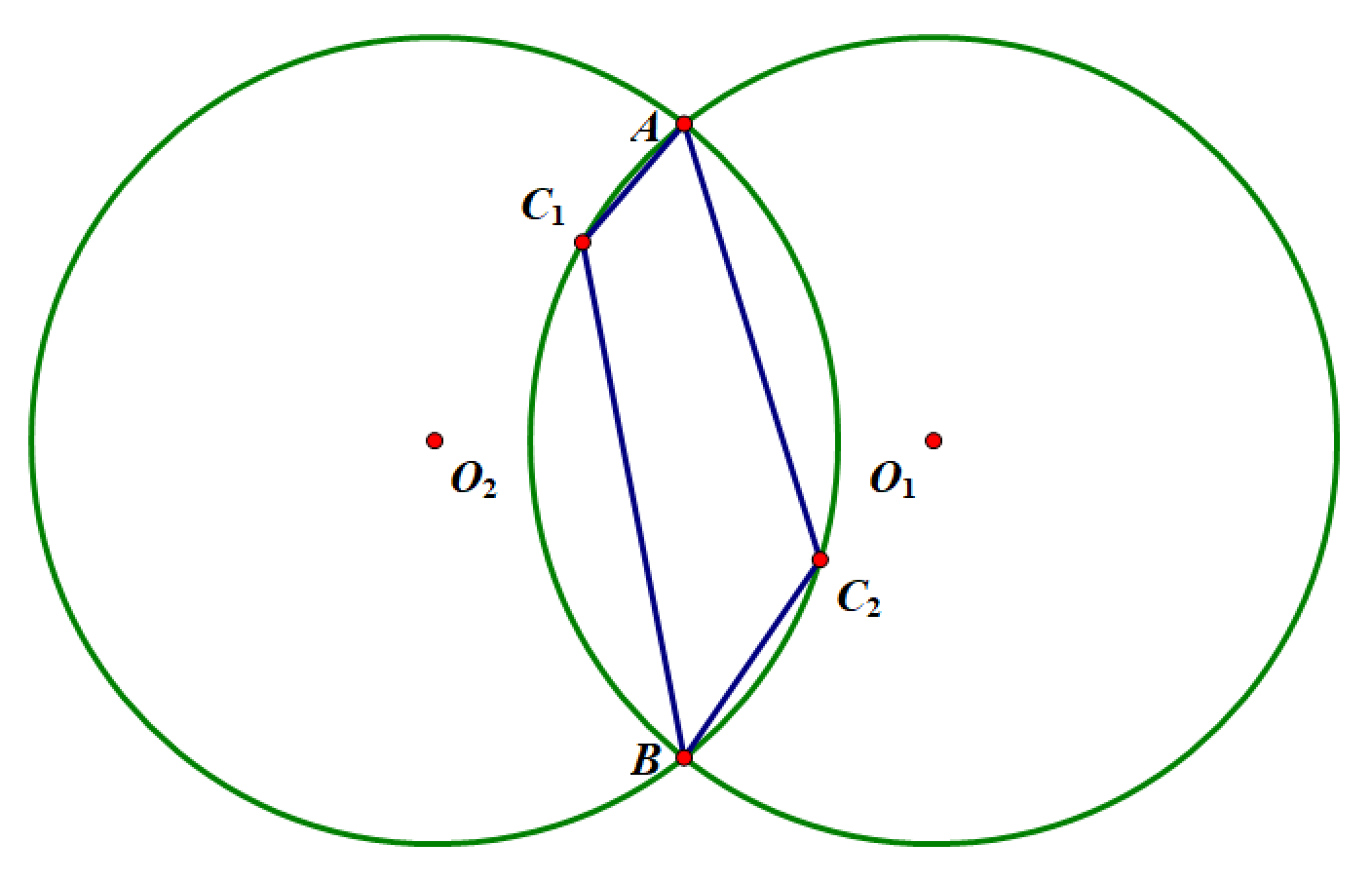
那么，$\cos\angle ACB=\frac{\vec{CA}\cdot\vec{CB}}{|CA||CB|}$，如果把$A,B,C$当成复数$a,b,c$，那么$\frac{c-a}{c-b}$的辐角为定值。

例子

首先，可以思考一下复数的conic section。

椭圆 / ellipse: $|c-a|+|c-b|$为常数

双曲线 / hyperbola: $(|c-a|-|c-b|)^2$为常数