The 2022 ICPC Asia Hong Kong Regional

A. TreeScript

你需要生成一棵给定的有根树，每个节点被创造的时候必须知道它的父节点的寄存器，并且在创造的时候可以将自己的地址丢到某一个寄存器中，初始情况下根的地址存在 \(r_0\) 里，求最少用多少寄存器。

考虑树上 DP，令 \(f(u)\) 表示以 \(u\) 为根的子树的答案，则有 \(f(u)=\max(f(v_1)+1, f(v_2)+1,\cdots,f(v_{k-1}) + 1, f(v_k))\)，其中 \(f(v_1)\sim f(v_k)\) 是从小到大排序的。

B. Big Picture

有一个 \(n+1\) 行，\(m+1\) 列的白色网格，对于每一行 \(i\)，有 \(p_{i,j}\) 的概率涂一个长度为 \(j\) 的前缀（\(1\leq j\leq m\)），对于每一列 \(i\)，有 \(q_{i,j}\) 的概率涂一个长度为 \(j\) 的前缀（\(1\leq j\leq n\)），求最终连通块数期望。

\(1\leq n,m\leq1000\)

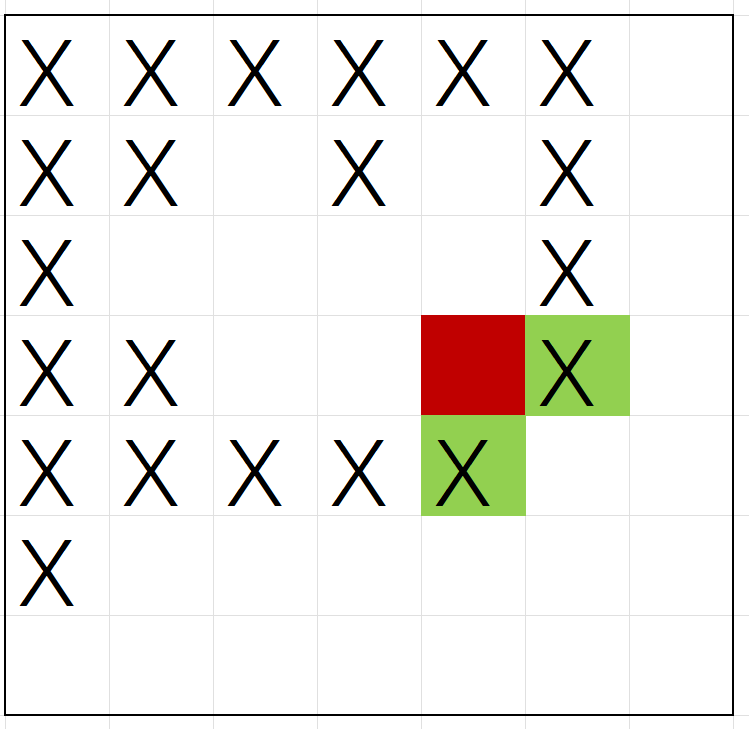
黑色连通块只有一个，每一个白色连通块内有且仅有一个格子满足其右边和下面的格子都是黑的，前缀和维护概率即可。

C. Painting Grid

给一个 \(n\) 行 \(m\) 列网格的每个格子涂上黑色或白色，使得黑色格子的数量等于白色格子的数量，并且每行的涂色方案两两不同，每列的涂色方案也两两不同。

\(n,m\leq 1000\)，多测。

首先特判掉 \(nm\) 为奇数的情况，然后不妨设 \(m\geq n\)。

\(n\) 位二进制数一共有 \(2^n\)，若 \(m>2^n\)，一定会重复，不存在方案，于是我们只需要对于 \(n\leq m\) 的情况构造方案即可。不妨先构造第 \(1\sim \lceil \log_2 m\rceil\) 行，考虑分治法，假设要填第 \(L\) 行第 \([l,r]\) 列，若区间长度是偶数，则前一半填 0，后一半填 1，否则0、1中哪个数少就多填一个，这样就可以保证在第 \(1\sim \lceil \log_2 m\rceil\) 行填完后 01 的差最多是 \(1\)，再填一行可以保证差恰好为 0。

再考虑补充到 \(n\) 行，此时每列一定是互不相同的，只需要保证各行互不相同即可。我们只需要在 \(2^m\) 行中挑出 \(n\) 行，且 \(n\leq m\)。只需要不断随机选一个串 \(T\)，然后把它及其反串填上去即可。当 \(m>20\) 的时候出错的概率忽略不计，\(m\leq 20\) 的情况下检查答案并且重 roll 的复杂度是可以接受的。

E. Goose, goose, DUCK?

给定数组 \(a\) 和整数 \(k\)，求有多少个区间满足不存在任意一个整数 \(x\)，使得 \(x\) 在该区间内 恰好出现 \(k\) 次。

对于每个整数 \(x\)，有若干组限制：若 \(l\in[L_1,R_1]\)，则 \(r\notin[L_2,R_2]\)。限制总数是 \(O(n)\) 的，然后就是经典扫描线。

F. Sum of Numbers

有一个大整数，由 \(1\sim9\) 租场，在里面插入 \(k\) 个加号，最后形成的表达式结果最小是多少。

\(1\leq k\leq 6\)

加号一定大致均分位数，每段长度可能为平均长度 +1，+0，-1。搜索即可。

H. Another Goose Goose Duck Problem

你要攻击 \(k\) 个怪物，每只怪物 \(b\) 秒出现一次，你可以钦定攻击间隔为 \([l,r]\) 中的一个数，一开始不可攻击，求全部击杀的用时。

选 \(l\) 最优，答案为 \(\lceil l/b\rceil\cdot b\cdot k\)。

K. Maximum GCD

给一个数组 \(a\)，进行任意次操作，每次操作任意选择 \((i,p)\)，然后 \(a_i\leftarrow (a_i\bmod p)\)。求最后整个数组的 \(\gcd\) 最大可能为多少，且 \(a_i\neq 0\)。

从小到大排序，然后去重，\(\bmod p\) 这个操作等价于让 \(a_i\) 变成 \(1\sim \lfloor\frac{a_i-1}2\rfloor\) 中的任意一个数。显然答案在 \([\lfloor\frac{a_1-1}2\rfloor,a_1]\) 内。任意一个答案可以等效为对前缀 \(1\sim p\) 求一个 \(\gcd\)，然后与 \(1\sim \lfloor\frac{a_{p+1}-1}2\rfloor\) 找一个最大的 \(\gcd\)。但是答案在 \([\lfloor\frac{a_1-1}2\rfloor,a_1]\) 内，于是这个前缀 gcd 必然是 \(a_1\) 或 \(a_1 / 2\) 才有可能成为答案。你只需要判断答案是否为 \(a_1\) 或 \(a_1/2\) 即可。

• 若 \(\lfloor\frac{a_2-1}2\rfloor\geq a_1\) 或 \(a_2=2a_1\)，即 \(a_2\geq 2a_1\) 时答案取 \(a_1\)。
• 若 \(a_1\) 为偶数，一定可以取 \(a_1/2\)，因为 \(a_2\geq a_1+1=2d+1\)，因此减一除二之后恰好为 \(a_1/2\)。
• 其余情况为 \((a_1-1)/2\)。

L. Delete Permutation

给一个排列 \(a\)，要删除一些元素，使其变成数组 \(b\)，有 \(k\) 个删除工具，每个工具可以选择一个长度为 \(l_i\) 的区间，删掉里面最大的数，每个工具只能用一次。求是否能够删成数组 \(b\)。

由于是排列，所以删除方案是唯一的，每次删掉最大的一个就可以了。用 multiset 维护工具，并用树状数组维护剩余的数，模拟以上过程。