2024 ICPC Asia Pacific Championship 【9】

本场比赛链接：link

H Pho Restaurant

给定 \(n\) 个 01 串，你可以选择某个串的某个字符移到另一个串的某个位置，最小化把所有串变成全 0 或全 1 串的操作次数。

\(2\leq n\leq 10^5, 1\leq |S_i|\leq 5\times10^5\)

题解

每个串可以抽象成其 01 字符的个数 $(a_i,b_i)$。对于每个字符串可以选择去掉所有的 $0$ 或者去掉所有的 $1$。贪心的答案是 $\sum \min(a_i,b_i)$，但是还需要保证有能够接收的转移字符的串，具体来说需要维护是否需要有接受 0 / 1 字符的串和是否存在能够提供 0 / 1 字符的串。

若供需不平衡，需要把答案加上 \(\min(|a_i-b_i|)\)。

J There and Back Again

给一张无向带权图，若两条路径 \(1\rightsquigarrow n\) 的边集不同，求它们路径长度和的最小可能是多少。

\(2\leq n\leq 10^5, 1\leq m\leq 3\times 10^5\)

题解

跑一遍最短路，枚举不在最短路上的边 $(u, v)$，用 $dis(1,u) + dis(v,n) + w_{(u,v)}$ 更新答案。

E Duplicates

给一个 \(n\times n\) 的数表，每个数都是 \(1\sim n\) 中的一个，每次操作可以选定 \(k, x, y\in[1, n]\)，把 \(a_{x,y}\) 修改为 \(k\)。求最少多少次修改能够使得每一行每一列都 不是 一个排列。

\(1\leq n\leq 100\)

题解

也可以考虑 $O(n^2)$ 做法。

有若干行 \(r_1,r_2,\cdots,r_N\) 和若干列 \(c_1,c_2,\cdots,c_M\) 是一个排列。每行至少改一次，每列也至少改一次，所以构造出 \(\max(N,M)\) 次操作即可。

设 \(N\leq M\)，把 \(a_{r_1,c_1}, a_{r_2, c_2}, \cdots, a_{r_N, c_N}\) 全都随便改成另一个数。问题转化成只有若干列的是排列。这种情况下不能随便改，可能导致改数的那一行从非排列变成排列。

一种解决方式是找到第一行出现最多的两个数字 \((i, j)\)，把 \(a_{1, c_{N+1}}, a_{1, c_{N+2}}, \cdots, a_{i, c_{M}}\) 改成 \(i, j\) 中异于自己的一个。这样第一行出现次数最少的数一定是 \(0\)。随便实现都是 \(O(n^2)\) 的。

C Bit Counting Sequence

已知长度为 \(n\) 的数列 \(x, x+1,x+2,\cdots, x+n-1\) 每一位的 \(\operatorname{popcount}\) 分别为 \(a_1,a_2,\cdots,a_n\)，求自然数 \(x\) 的最小值。

\(0\leq a_i\leq 60, \sum n\leq 5\times 10^5\)

题解

差分之后逐步确定，若 $x$ 二进制末尾有连续 $c$ 个 $1$，那么 $+1$ 后 $\operatorname{popcount}$ 会减少 $1-c$。因此扫一遍差分数组 $d_i$，并维护一次次 +1 的过程。每步可以确定它的末 $2-d_i$ 位一定是一个 $0$ 后跟 $1-d_i$ 个 $1$。最后如果没有出现矛盾，会知道一个 $x+n-1$ 的后缀，为了保证 $\operatorname{popcount}$ 是对的，需要把 $1$ 填在未确定的最低位上。

G Personality Test

给 \(n\) 个长度为 \(m\) 的字符串，\(s_1, s_2, \cdots, s_n\)，若 \((i, j)\)，满足至少有 \(k\) 个下标 \(p\) 使得 \(s_{ip} = s_{jp}\) 且 \(s_{ip} \neq {\textrm {'.'}}\)。求 \(j\) 最小的情况下最大的 \(i\)。

\(2\leq n\leq 5000, 1\leq m\leq 3000, 1\leq k\leq \color{red}5\)，5秒

题解

看看你的暴力水平。

读完所有的字符串，然后枚举位置 \(1\sim m\)，同字符的串形成一个个团，计算贡献。这种方法即使有剪枝也不一定能通过。一种比较好的做法是动态的加入每个字符串，查询新加入的串是否能够和已有的串形成配对。由抽屉原理，最多枚举约 \(4n^2\) 条边，这是可以通过的，而前者不能保证第一次枚举到的就是答案，因此不能通过。

F Forming Groups

给定一个长度为 \(n\) 的序列，任选一个 \(r\) ，把 \(a_0\) 移到 \(a_r(0\leq r < n )\) 右边，选一个 \(n\) 的因数 \(k(k>1)\)，把 \(a_0,a_1,\cdots,a_{n-1}\) 按下标模 \(k\) 的结果分成 \(k\) 组。最小化每组中数字和的最大值和最小值的比值，输出精确分数。

\(2\leq n\leq \sum n\leq10^6, 1\leq a_i\leq 1000\)

题解

考虑枚举 \(k, r\)，固定 \(k\) ，枚举 \(r\) 的过程等价于执行 \(n\) 次相邻对换，每次相邻对换最多改变两个和，利用 multiset 或者 priority_queue 维护最值即可。

实际上只需要枚举 \(k\) 是质数的情况，因为 \(c\cdot k\) 组变成 \(k\) 组是一个只有合并的过程，合并会导致每一组的平均数向中间值靠近，答案会变优。

时间复杂度 \(O(\omega(n)\cdot n\log n)\)

K Tree Quiz

给一个 \(n\) 个节点的树，把所有 \(n^2\) 点对 \((x, y)\) 按照 \(x\) 为第一关键字，\(\operatorname{LCA}(x, y)\) 为第二关键字， \(y\) 为第三关键字从小到大排序，\(q\) 次询问排序后排在第 \(k\) 的点对是什么。

\(1\leq n,q\leq 10^5\)

题解

数据结构套路题，会的选手挺多。

\(x\) 是可计算的，LCA 一定是根到 \(x\) 路径 \(p_1,p_2,\cdots,p_c\) 上的一点，对于节点 \(p_i\)，共有 \(sz_{p_i}-sz_{p_{i+1}}\) 个 \(y\) 满足 \(\operatorname{LCA}(x, y)=p_i\)，定义其为 \(f(p_i)\)。考虑 dfs 的过程中利用权值线段树维护数组 \(f\)，线段树上二分便可定位出 LCA。

再考虑已知 LCA 与 \(x\) 如何定位 \(y\)，设 \(\operatorname{LCA}(x, y)=z\)，即求 \(subtree(z)\backslash subtree(u)\)，其中 \(u\) 是 \(x\) 的祖先，\(z\) 的儿子。考虑利用权值线段树维护子树集合，线段树合并自底向上合并上去。询问便是两个线段树做差，同样的线段树上二分便可定位 \(y\)。

时间复杂度为 \(O((n+q)\log n)\)

线段树合并的复杂度是 \(O(\sum |T| - |\sum T|)\)，初始有 \(n\) 个 \(\log\) 个节点的树，最后变成一个 \(n\) 个节点的树，因此复杂度为 \(O(n\log n)\)。

I Symmetric Boundary

给定一个凸包的所有顶点，找一点 \(P\) ，作所有点关于 \(P\) 的对称点，若存在一个凸包使得这两组点都在凸包上，求该凸包的面积最小值。

\(3\leq n\leq 30, 0\leq x_i,y_i\leq 1000\)

题解

原凸包上点的相对顺序在新凸包上不变。

大胆猜测凸包面积取最小值时新凸包一定存在三点共线的情况，因此这三点中的两点是一条原凸包上的边。

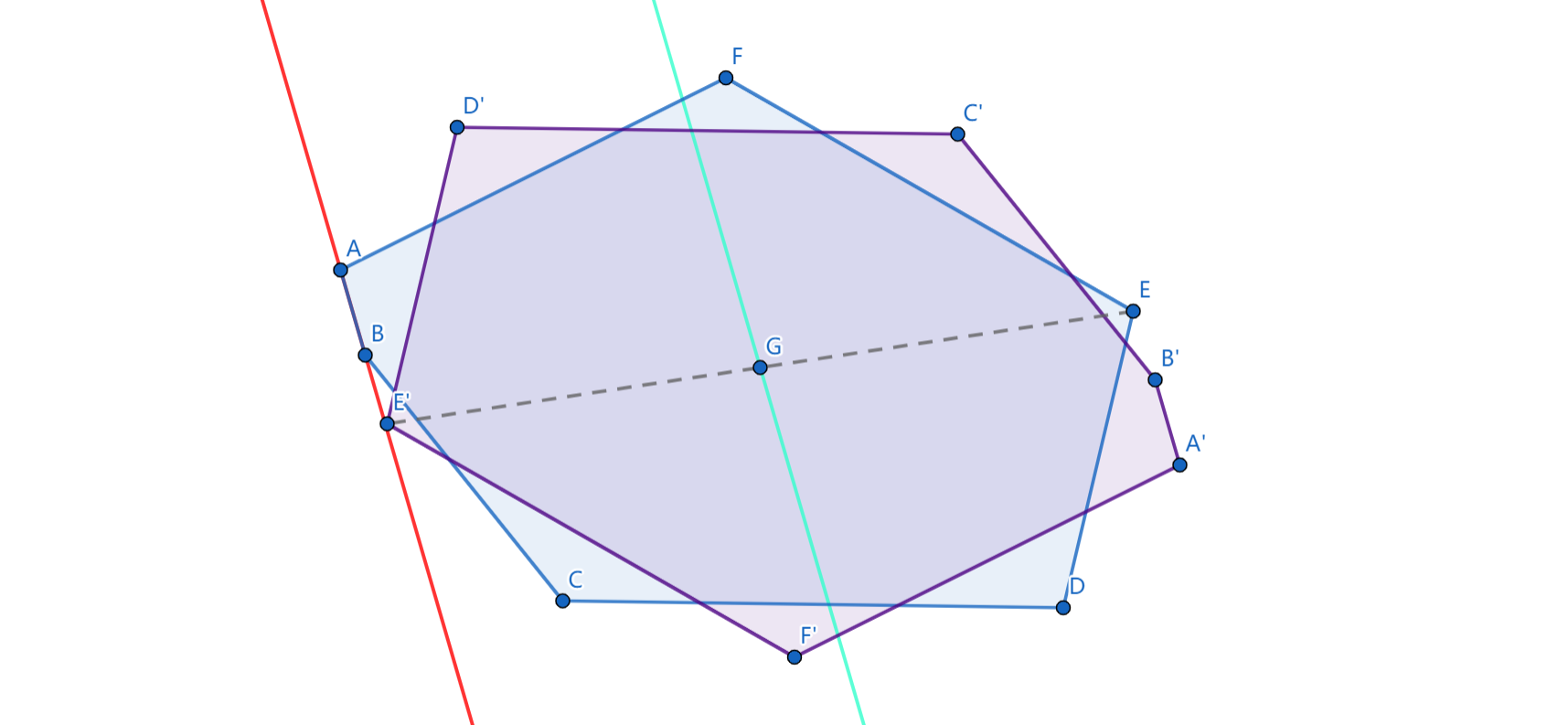
枚举每条边 \((a_i,a_{i+1})\)，再枚举另一点 \(a_j\)，则对称中心一定在这个三角形中 \((a_i,a_{i+1})\) 的中位线上。枚举任意两条线可以确定所有可能的对称中心，再对每个对称中心求一次凸包便可计算出答案。

时间复杂度 \(O(n^5\log n)\)

为什么这么做是对的？ 一种理解是考虑上面提到的直线将平面分割成若干个区域，在相同区域内部选择的对称中心形成的凸包点的顺序是相同的，现在考虑对凸包求曲线积分的过程，每一段都是关于对称中心坐标的线性函数，因此最后取极值的地方一定在顶点上。

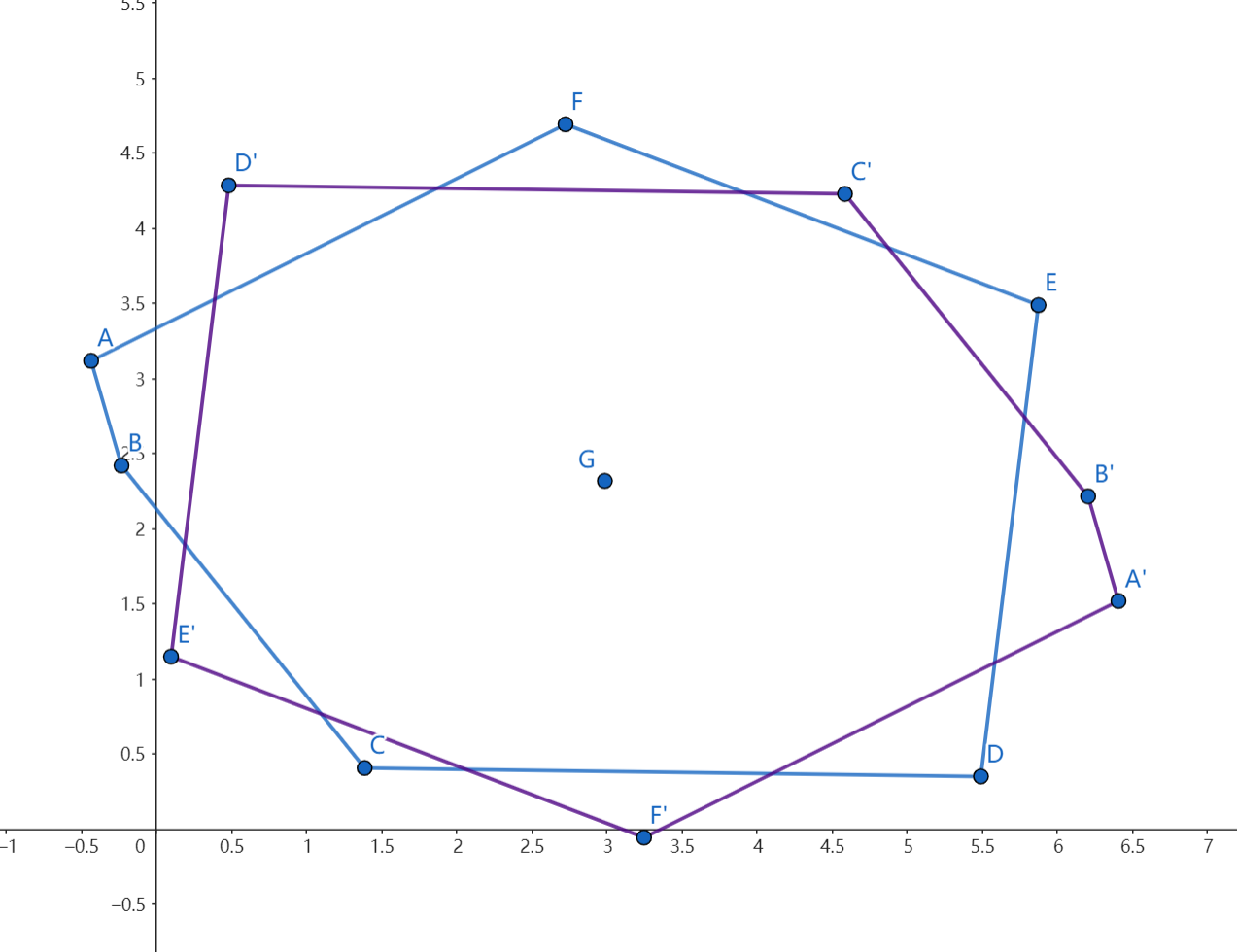
实现的时候需要注意，凸包可以是非严格的（接受共线），所以极角相同的情况下需要按照距离从小到大排序，并且排完序后与最后一条边共线的几个点顺序需要调换。好一点的实现是以对称中心为原点的极角排序。

    int p = ret.size() - 1;
    while(p > 0 && turn_left(ret[0], ret[p - 1] , ret[p]) ==0){
        -- p;
    }
    reverse(ret.begin() + p, ret.end());

L XOR Operations

给一个数组 \(a_1,a_2,\cdots,a_n\)，令数组 \(b_1,\cdots,b_n\) 全零，进行任意次操作，每次操作选择 \(i,j\)，然后令 \(b_i\leftarrow b_i\oplus a_i\oplus a_j\)，\(b_j\leftarrow b_j\oplus a_i\oplus a_j\)。求数组 \(b\) 可能出现的所有可能值，对 \(998244353\) 取模。

\(2\leq n\leq 2\times 10^5\)，\(0\leq a_i<2^{30}\)

题解

最终每一个 \(b_i\) 一定是偶数个 \(a_j\) 的异或和。先求出数组 \(a_{i}\oplus a_{i+1}\) 的异或线性基，设其大小为 \(k\)。考虑第 \(i\) 位 \(b_i\) 可能是多少，例如 \(b_1\) 的方案有 \(2^k\) 种，当钦定 \(b_1\) 之后，钦定后面的数便不可再次使用 \(a_1\) 了，因为这势必导致 \(b_1\) 的变化。

由于选 \(c\) 个数时对答案的贡献为 \(2^{\min(c, k)}\) 所以答案为 \(2^{\sum \min(i,k)}\)。