机器学习实战(阶段一)--2.线性回归
1、线性回归模型概念
线性回归模型能够用一个直线较为精确地描述数据之间的关系。当出现新的数据的时候,就能够预测出一个简单的值。
2、损失/代价函数介绍
通过线性回归算法,可能会得到很多的线性回归模型,但是不同的模型对于数据的拟合或者是描述能力是不一样的。我们的目的最终是需要找到一个能够最精确地描述数据之间关系的线性回归模型。损失/代价函数就是用来描述线性回归模型与正式数据之前的差异。如果完全没有差异,则说明此线性回归模型完全描述数据之前的关系。如果需要找到最佳拟合的线性回归模型,就需要使得对应的损失/代价函数最小。
3、实现流程

4、简单实现
4.1. 获取数据。数据采用sklearn自带的波士顿房价数据集(Boston)。
#boston房价数据集 boston = load_boston()
波士顿房价数据集(Boston)位于../Python37/Lib/site-packages/sklearn/datasets/data/boston_house_prices.csv文件,共计506条数据。
每条数据包含房屋以及房屋周围的详细信息。前13列为可能影响房价的特征值boston.data,第14列为目标房价boston.target。
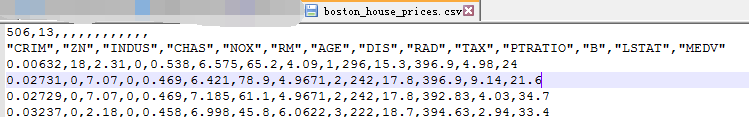
CRIM:城镇人均犯罪率
ZN:住宅用地超过 25000 sq.ft. 的比例
INDUS:城镇非零售商用土地的比例
CHAS:查理斯河空变量(如果边界是河流,则为1;否则为0)
NOX:一氧化氮浓度
RM:住宅平均房间数
AGE:1940 年之前建成的自用房屋比例
DIS:到波士顿五个中心区域的加权距离
RAD:辐射性公路的接近指数
TAX:每 10000 美元的全值财产税率
PTRATIO:城镇师生比例
B:1000(Bk-0.63)^ 2,其中 Bk 指代城镇中黑人的比例
LSTAT:人口中地位低下者的比例
MEDV:自住房的平均房价,以千美元计
#通过DESCR属性可以查看数据集的详细情况,这里数据有14列,前13列为特征数据,最后一列为标签数据。 #print(boston.DESCR) #boston的data和target分别存储了特征和标签 #print(boston.data) #print(boston.target)
4.2. 切分数据。
#切分数据集 X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=2)
test_size=测试集的比例
random_state=随机数种子,保证程序的可重复性
4.3 运行线性模型。选用sklearn中基于最小二乘的线性回归模型,并用训练集进行拟合,得到拟合直线y=wTx+b中的权重参数w和b:
#简单线性回归 model1 = LinearRegression(normalize=True) model1.fit(X_train, y_train)
4.4 模型测试。利用测试集得到对应的结果,并利用均方根误差(MSE)对测试结果进行评价:
#模型的拟合值 y_pred=model1.predict(X_test) print("MSE:",metrics.mean_squared_error(y_test, y_pred))
4.5 模型的拟合优度
#模型的拟合优度 simpleScore=model1.score(X_test, y_test) print(simpleScore)
4.6 交叉验证。使用10折交叉验证,即cv=10,并求出交叉验证得到的MSE值
#交叉验证 predicted=cross_val_predict(model1, boston.data, boston.target, cv=10) print ("MSE:", metrics.mean_squared_error(boston.target, predicted))
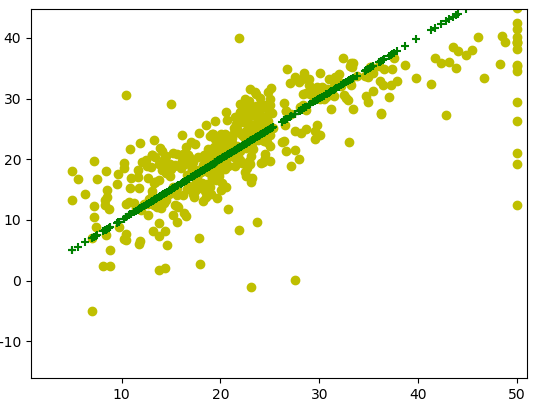
4.7.输出图像。将实际房价数据与预测数据作出对比,接近中间绿色直线的数据表示预测准确
#画图 import matplotlib.pyplot as plt plt.scatter(boston.target, predicted, color="y", marker="o") plt.scatter(boston.target, boston.target, color="g", marker="+") plt.show()
5、多项式线性回归
5.1. 同4.1
5.2. 同4.2
5.3. 增加特征多项式让线性回归模型更好地拟合数据.多项式的个数的不断增加,可以在训练集上有很好的效果,但很容易造成过拟合。
poly = PolynomialFeatures(degree=2, include_bias=False) X_train_poly =poly.fit_transform(X_train) X_test_poly =poly.fit_transform(X_test)
degree:多项式特征的个数,默认为2
include_bias:默认为True,包含一个偏置列,也就是用作线性模型中的截距项
5.4. 运行线性模型。
#多项式线性回归
model2 = LinearRegression(normalize=True)
model2.fit(X_train_poly, y_train)
fit_intercept:默认为True,是否计算截距项。
normalize:默认为False,是否对数据归一化
5.5. 模型测试。利用测试集得到对应的结果,并利用均方根误差(MSE)对测试结果进行评价:
#模型的拟合值
y_pred=model2.predict(X_test_poly)
print("MSE:",metrics.mean_squared_error(y_test, y_pred))
5.6. 模型的拟合优度
#模型的拟合优度
mutilScore=model2.score(X_test_poly, y_test)
print(mutilScore)
5.7. 交叉验证。使用10折交叉验证,即cv=10,并求出交叉验证得到的MSE值
#交叉验证
predicted=cross_val_predict(model2, boston.data, boston.target, cv=10)
print ("MSE:", metrics.mean_squared_error(boston.target, predicted))
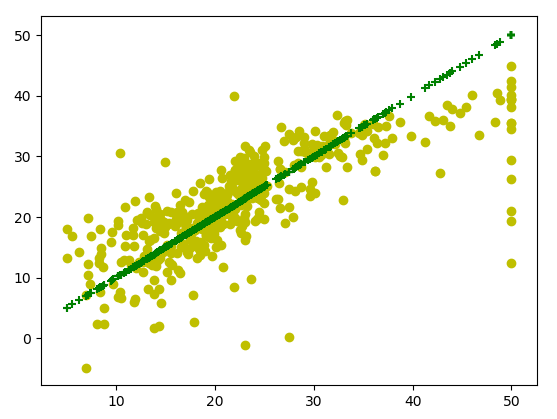
5.8.输出图像。将实际房价数据与预测数据作出对比,接近中间绿色直线的数据表示预测准确
#画图
import matplotlib.pyplot as plt
plt.scatter(boston.target, predicted, color="y", marker="o")
plt.scatter(boston.target, boston.target, color="g", marker="+")
plt.show()
本例源码:https://github.com/jhw111/mllearn



 浙公网安备 33010602011771号
浙公网安备 33010602011771号