神经网络_2

1. 左边蓝色的圆圈叫“输入层”，中间橙色的不管有多少层都叫“隐藏层”，右边绿色的是“输出层”。

2. 每个圆圈，都代表一个神经元，也叫节点(Node)。

3. 输出层可以有多个节点，多节点输出常常用于分类问题。

4. 理论证明，任何多层网络可以用三层网络近似地表示。

(2) 激活函数

 1. Sigmoid(S形曲线)

    

    

（3）计算方法

      

      

 

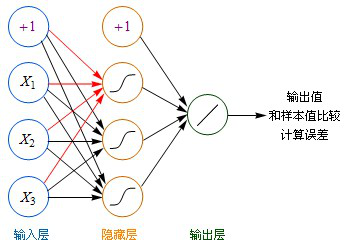
 1. +1代表偏移值(偏置项, Bias Units)

 2. 隐藏层用都是用Sigmoid作激活函数，而输出层用的是Purelin。

 3. 起初输入层的数值通过网络计算分别传播到隐藏层，再以相同的方式传播到输出层，最终的输出值和样本值作比较，计算出误差。

  

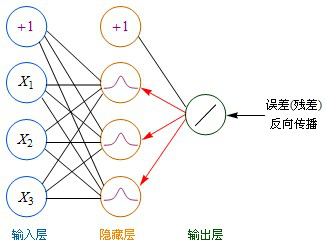
 4. 计算残差：

    残差(error term)：误差的偏导数。

    Purelin的导数=1

    Sigmoid导数 = Sigmoid*(1-Sigmoid) 

    输出层→隐藏层：残差 = -(输出值-样本值) * 激活函数的导数 
    隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 激活函数的导数

 

    输出层→隐藏层：Purelin作激活函数，残差 = -(输出值-样本值)

                                Sigmoid作激活函数，残差 = -(Sigmoid输出值-样本值) * Sigmoid*(1-Sigmoid) = -(输出值-样本值)输出值(1-输出值)

    隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 当前节点的Sigmoid*(1-当前节点的Sigmoid)

  5. 跟新权重：

    输入层：权重增加 = 当前节点的Sigmoid * 右层对应节点的残差 * 学习率 
   隐藏层：权重增加 = 输入值 * 右层对应节点的残差 * 学习率 
   偏移值的权重增加 = 右层对应节点的残差 * 学习率

     

    隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 当前节点的Sigmoid*(1-当前节点的Sigmoid)

（4）优缺点

    缺点：计算复杂、计算速度慢、容易陷入局部最优解