决策树2

熵(entropy) 是表示随机变量不确定性的度量（纯度），如果信息的不确定性越大，熵的值也就越大

信息增益(information gain)：表示由于特征A使得对数据集D的分类的不确定性减少的程度。==》max

基尼指数：一个节点越“纯”，也就是说这个节点的样本越多属于同类，那么Gini指标越小==》min

cart有两种评价标准：Variance和Gini系数。

而ID3和C4.5的评价基础都是信息熵。

信息熵和Gini系数是针对分类任务的指标，而Variance是针对连续值的指标因此可以用来做回归。

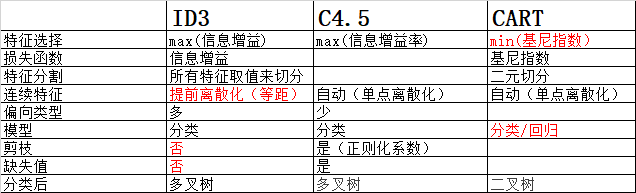
1.ID3

一旦按某特征切分后，该特征在之后的算法执行中，将不再起作用

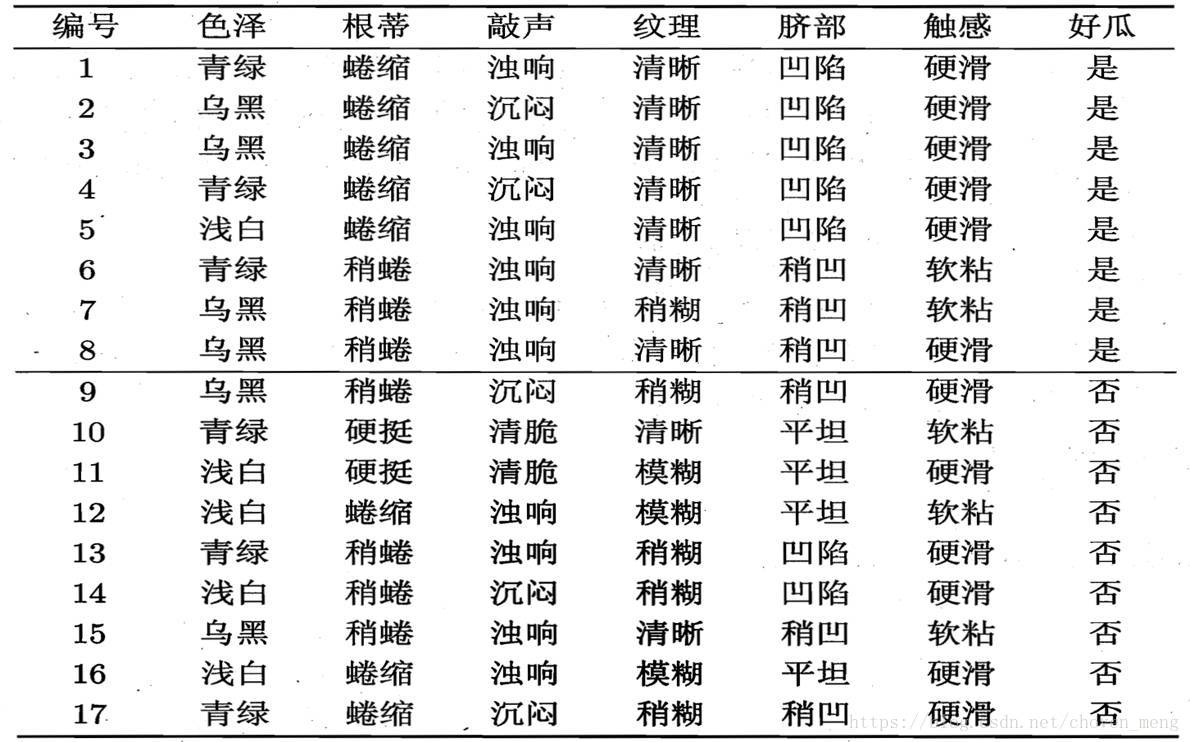
类似的，我们可以计算出其他属性的信息增益，选取信息增益最大的进行划分，依次类推，最终得到决策树：

2.C4.5

信息增益和特征熵的比值，特征数越多的特征对应的特征熵越大，它作为分母，可以校正信息增益偏向取值较多的特征的问题。

与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

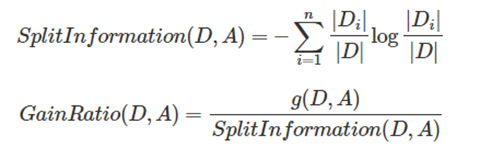
1.计算其信息熵：
Info(D) = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940

2.对属性集中每个属性分别计算信息熵
Info(OUTLOOK) = 5/14 * [- 2/5 * log2(2/5) – 3/5 * log2(3/5)] +
4/14 * [ - 4/4 * log2(4/4) - 0/4 * log2(0/4)] +
5/14 * [ - 3/5 * log2(3/5) – 2/5 * log2(2/5)] = 0.694

3.信息增益值
Gain(OUTLOOK) = Info(D) - Info(OUTLOOK) = 0.940 - 0.694 = 0.246

4.计算分裂信息度量SplitInfo,此处记为H(V)：
H(OUTLOOK) = - 5/14 * log2(5/14) - 5/14 * log2(5/14) - 4/14 * log2(4/14) = 1.577

5.计算信息增益率，如下所示：
IGR(OUTLOOK) = Info(OUTLOOK) / H(OUTLOOK) = 0.246/1.577 = 0.155

3.CART

CART对于分类问题选用基尼指数作为损失函数，对于回归问题使用平方误差作为损失函数。

ID3，C4.5再迭代创建树节点时，每个特征只能出现一次，但CART可以出现多次，这也是为什么CART能够进行回归。

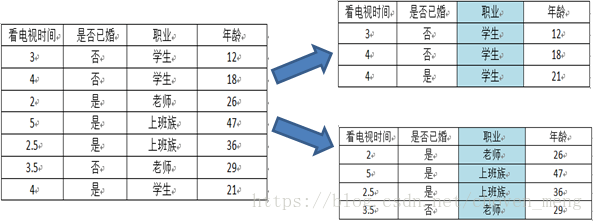
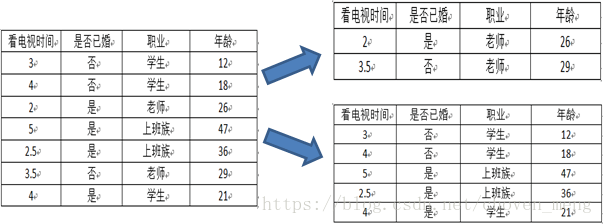
3.1 CART是回归树时，用最小方差选择最优特征

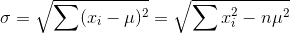
3.2 CART分类时，用基尼指数选择最优特征

4.决策树停止生长的条件

（1）最小节点数

当节点的数据量小于一个指定的数量时，不继续分裂。两个原因：一是数据量较少时，再做分裂容易强化噪声数据的作用；二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。

（2）熵或者基尼值小于阀值。

由上述可知，熵和基尼值的大小表示数据的复杂程度，当熵或者基尼值过小时，表示数据的纯度比较大，如果熵或者基尼值小于一定程度数，节点停止分裂。

（3）决策树的深度达到指定的条件

节点的深度可以理解为节点与决策树跟节点的距离，如根节点的子节点的深度为1，因为这些节点与跟节点的距离为1，子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度，当深度到达指定的上限大小时，停止分裂。

(4）所有特征已经使用完毕，不能继续进行分裂。

5.连续值

ID3原本是没有处理能力连续型数据，只有通过离散化将连续性数据转化成离散型数据再进行处理。这里采用简单的等距离数据划分的方法。该方法先对数据进行排序，然后将连续型数据划分为多个区间，并使每一个区间的数据量基本相同，再以划分的区间进行分类。

c4.5和cart：采用单点离散化对连续型特征进行处理

比如，m个样本的连续特征A有m个，从小到大排列为a1,a2,a3......am,则C4.5取相邻两样本值的平均值，一共取得m-1个划分点，其中第i个划分点表示 $T_i = \frac{a_i + a_{i+1}}{2}$ ,对于这m-1个划分点，分别计算以该点作为二元分类点的信息增益，以信息增益最大的点作为该连续特征的二元离散分类点