PCA

通过正交变换将一组相关性的变量数据转换为一组线性不相关的变量，转换后的变量被称为主成分。

将n维样本点转换为k维后，每一维上的样本方差都很大。

1.特征值和特征向量

A为n×n的方阵且有 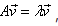    其中λ为一标量，则称λ为向量v对应的特征值，也称v为特征值λ对应的特征向量。

2.对角矩阵

对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag（a1，a2,...,an) 。

3.方差矩阵

 

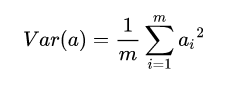
 4.协方差矩阵

 

 

 

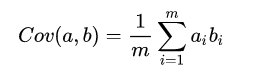
  5.PCA推导

 

   6.PCA算法流程

从上面两节我们可以看出，求样本  的  维的主成分其实就是求样本集的协方差矩阵  的前  个特征值对应特征向量矩阵  ，然后对于每个样本  ,做如下变换  ，即达到降维的PCA目的。

下面我们看看具体的算法流程：

输入：  维样本集  ，要降维到的维数  .

输出：降维后的样本集 

1.对所有的样本进行中心化 

2.计算样本的协方差矩阵

3.求出协方差矩阵的特征值及对应的特征向量

4.将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

5.Y=PX即为降维到k维后的数据