FM

https://www.cnblogs.com/wkang/p/9588360.html

一、FM背景

FM(Factorization Machine)主要目标是：解决数据稀疏的情况下，特征怎样组合的问题。

以一个广告分类的问题为例，根据用户画像、广告位以及一些其他的特征，来预测用户是否会点击广告（二分类问题）。数据如下：

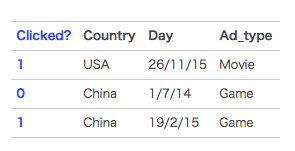
将上面的离散特征数据进行one-hot编码以后（假设Country,Day,Ad_type类别只有图中几种），如下图所示 

 

 

 在一般的线性模型中，是各个特征独立考虑的，没有考虑到特征与特征之间的相互关系。但实际上，大量的特征之间是有关联的。

最简单的以电商为例，一般女性用户看化妆品服装之类的广告比较多，而男性更青睐各种球类装备。那很明显，女性这个特征与化妆品类服装类商品有很大的关联性，男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来，显然是很有意义的。

二、FM算法模型 

1、模型目标函数

    二元交叉的FM（2-way FM）目标函数如下：

    其中，w是输入特征的参数，<vi,vj>是输入特征i,j间的交叉参数，v是k维向量。

    前面两个就是我们熟知的线性模型，后面一个就是我们需要学习的交叉组合特征，正是FM区别与线性模型的地方。 

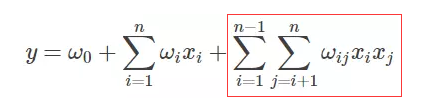
2、模型的计算复杂度

可能有人会问，这样两两交叉的复杂度应该O(k*n^2)吧，其实，通过数学公式的巧妙转化一下，就可以变成O(kn)了。

转化公式如下所示，其实就是利用了2xy = (x+y)^2 – x^2 – y^2的思路。  

 

 

 

 

 

 

3、模型的应用

    FM可以应用于很多预测任务，比如回归、分类、排序等等。

    1.回归Regression：y^(x)直接作为预测值，损失函数可以采用least square error；

    2.二值分类Binary Classification：y^(x)需转化为二值标签，如0,1。损失函数可以采用hinge loss或logit loss；

    3.排序Rank：x可能需要转化为pair-wise的形式如(X^a,X^b)，损失函数可以采用pairwise loss

4、模型的学习方法

    前面提到FM目标函数可以在线性时间内完成，那么对于大多数的损失函数而言，FM里面的参数w和v更新通过随机梯度下降SGD的方法同样可以在线性时间内完成，比如logit loss，hinge loss，square loss，模型参数的梯度计算如下： 

 

 

 

 

5、模型延伸：多元交叉

    前面提到到都是二元交叉，其实可以延伸到多元交叉，目标函数如下：（看起来复杂度好像很高，其实也是可以在线性时间内完成的） 

 

 

6、总结

前面简单地介绍了FM模型，总的来说，FM通过向量交叉学习的方式来挖掘特征之间的相关性，有以下两点好处：

1.在高度稀疏的条件下能够更好地挖掘数据特征间的相关性，尤其是对于在训练样本中没出现的交叉数据；

2.FM在计算目标函数和在随机梯度下降做优化学习时都可以在线性时间内完成。 

三、FM算法 VS 其他算法

1、FM 对比 SVM

1）SVM 

 

 

2）FM 对比 SVM

    a. SVM和FM的主要区别在于，

        SVM的二元特征交叉参数是独立的，如wij，而FM的二元特征交叉参数是两个k维的向量vi、vj，<vi,vj>和<vi,vk>是相互影响的。

         FM可以在原始形式下进行优化学习，而基于kernel的非线性SVM通常需要在对偶形式下进行；

         FM的模型预测是与训练样本独立，而SVM则与部分训练样本有关，即支持向量。 

    b. 为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢？

        线性svm只有一维特征，不能挖掘深层次的组合特征在实际预测中并没有很好的表现；

        多项式svn，交叉的多个特征需要在训练集上共现才能被学习到，否则该对应的参数就为0，这样对于测试集上的case而言这样的特征就失去了意义，

        FM通过向量化的交叉，可以学习到不同特征之间的交互，进行提取到更深层次的抽象意义。