GBDT

（1）Adaboost

最优的w

处理的粒度是更新参数w，使得损失函数L(y,f(x))最小 

 

 

 

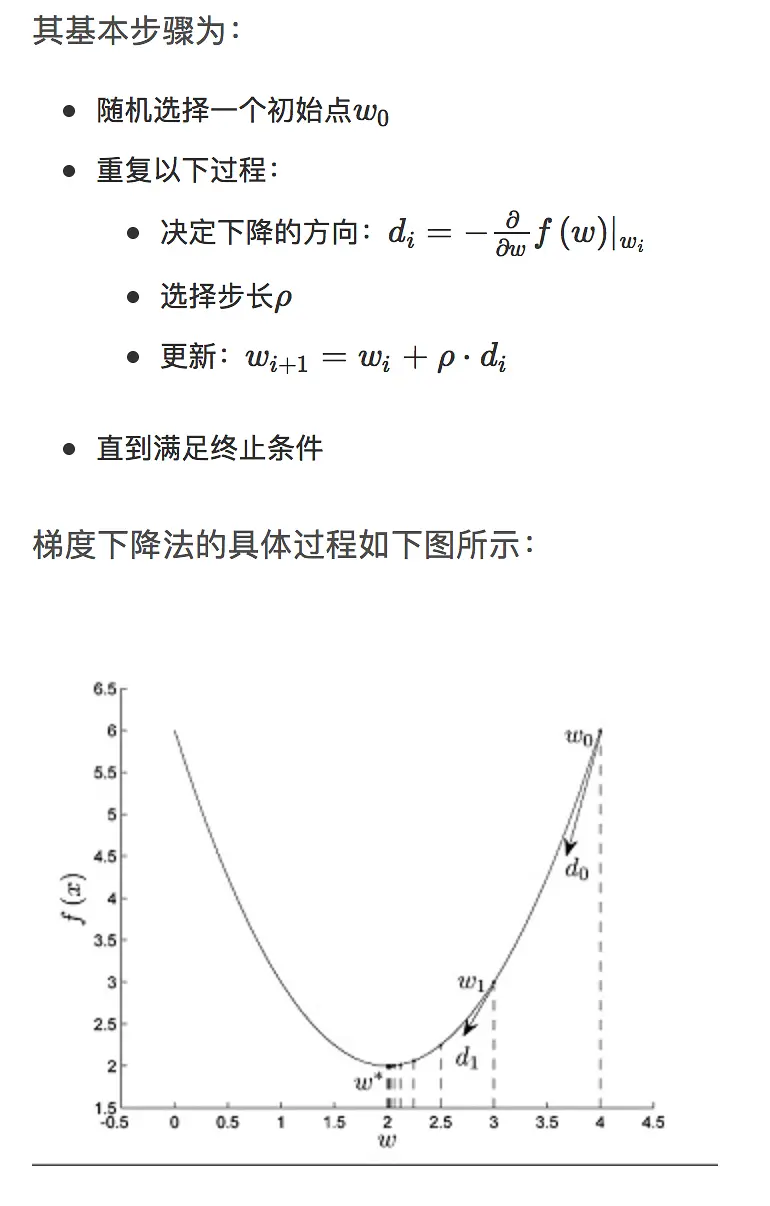
（2）GBDT

 

 

最优的函数F(X)

处理粒度是更新函数F(X)，使得损失函数L(y,F(X))最小。

 

 

 

 

 

 

 

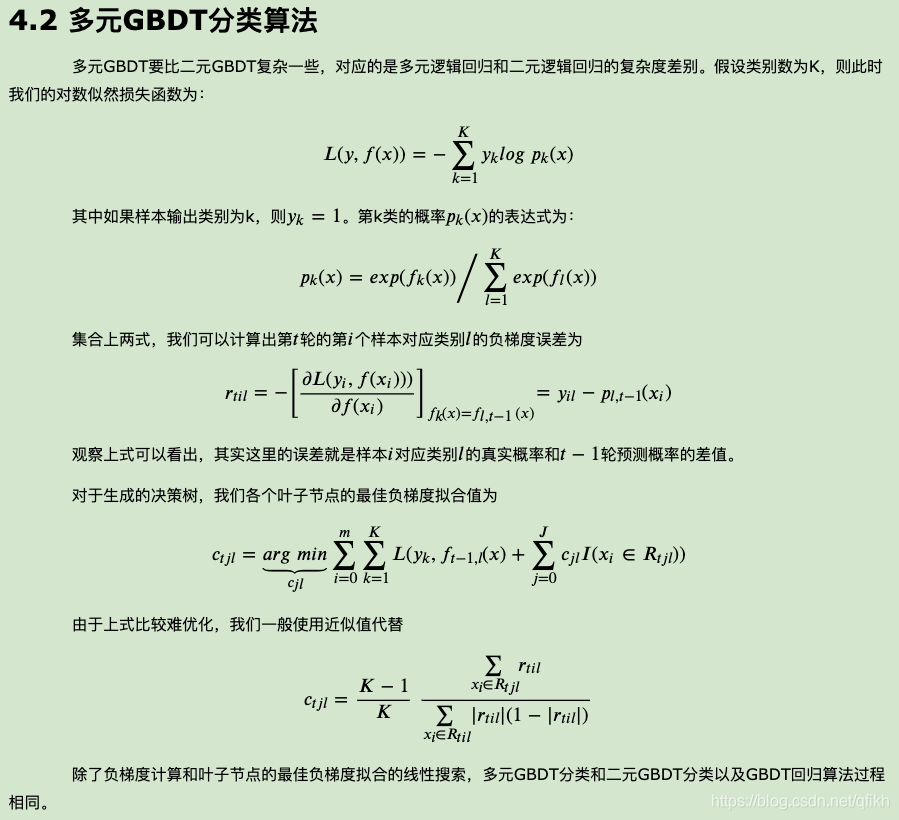
GBDT分为两种：

都是迭代回归树

每棵树都在学习前N-1棵树尚存的不足

都是累加每颗树结果作为最终结果

（1）残差版本 　 

残差迭代树，其核心思想是每轮通过拟合残差来降低损失函数。

优点：全局最优值，每一步都在试图让结果变成最好

缺点：由于它依赖残差，cost function一般固定为反映残差的均方差，很难处理纯回归问题之外的问题。

步骤：

在学习的过程中，首先学习一颗回归树，然后得到残差

把残差作为一个学习目标，学习下一棵回归树

依次类推，直到残差小于某个接近0的阀值或回归树数目达到某一阀值。

（2）梯度版本
梯度迭代树

Gradient是局部最优方向*步长，每步试图让结果更好一点

优点：只要可求导的cost function都可以使用。

（1）残差

 

 

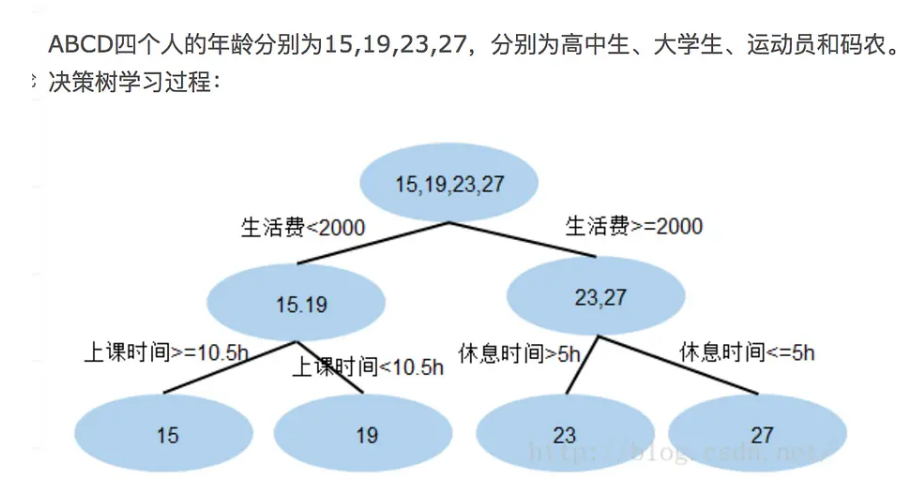
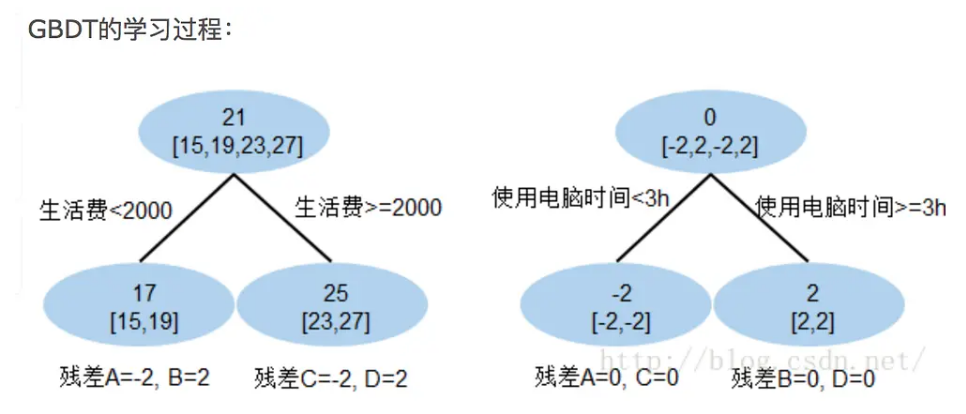
现在A,B,C,D的预测值都和真实年龄一致 A: 15岁高中学生，收入较少，天天没时间玩电脑；预测年龄A = 17– 2 = 15

B: 19岁大学生；收入较少，天天宅在宿舍玩电脑；预测年龄B = 17+ 2 = 19

C: 23岁运动员；收入较多，体育训练没时间玩电脑；预测年龄C = 25 – 2 = 23

D: 27岁码农；收入较多，长时间玩电脑；预测年龄D = 25 + 2 = 27

（2）梯度下降

 

 

 

 

 

 

 

 

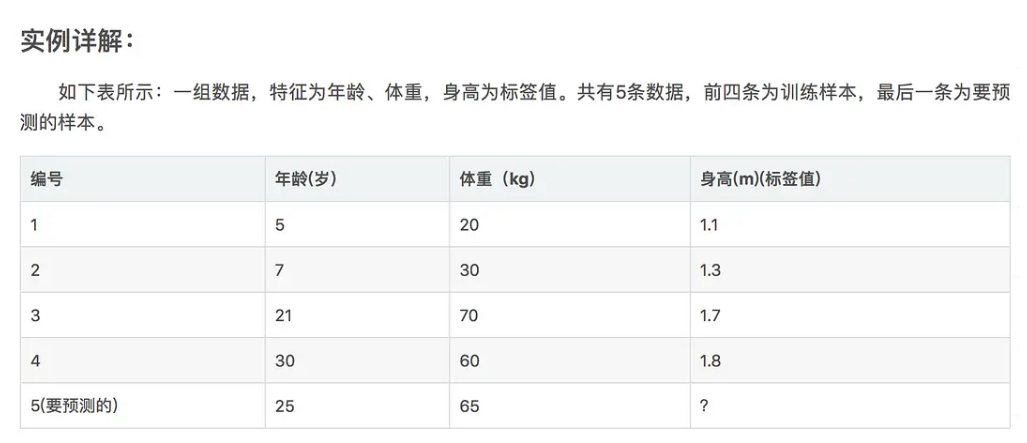
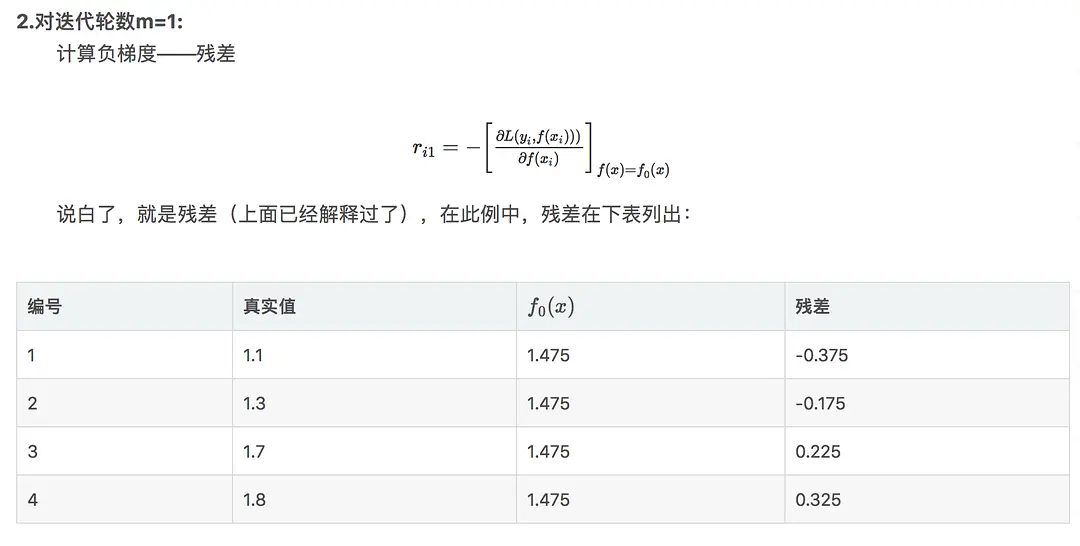
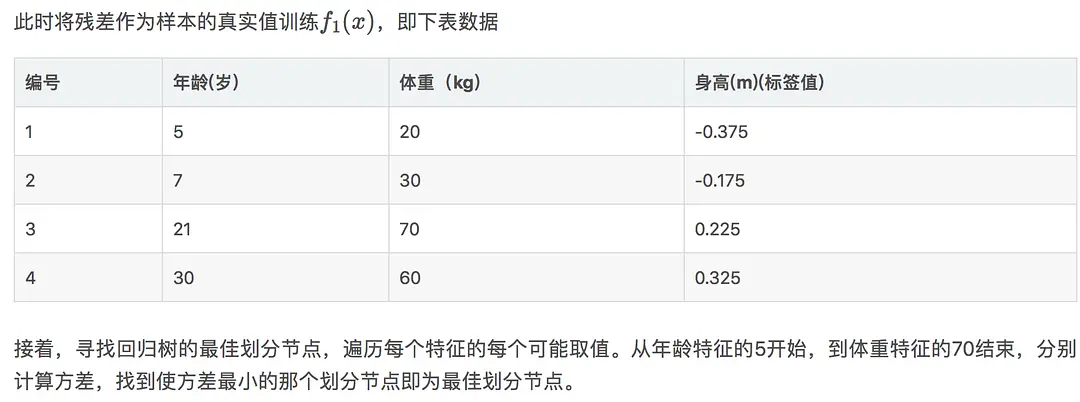
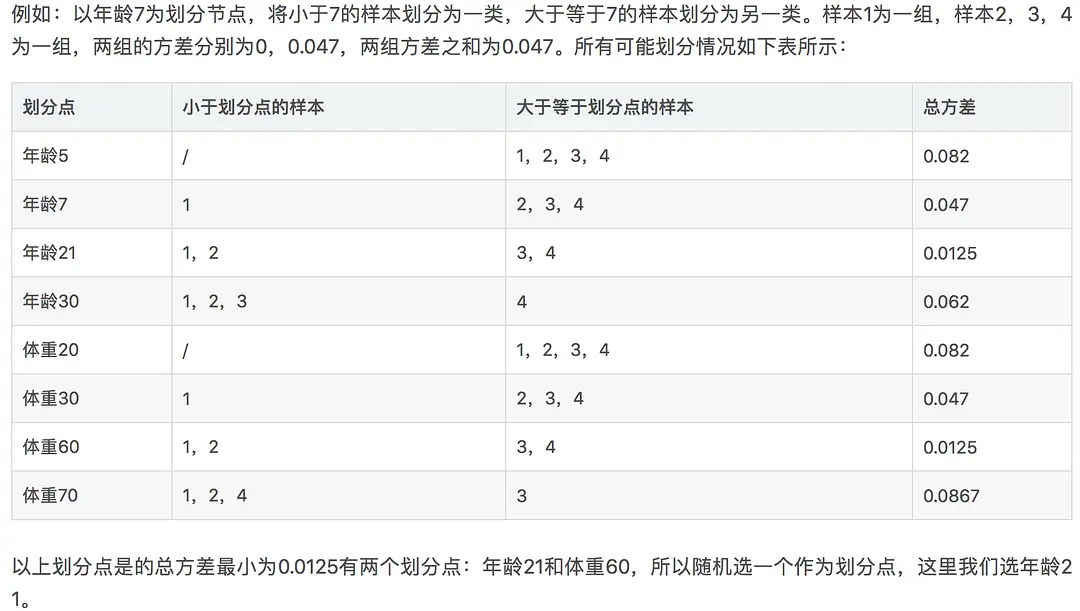
年龄7计算方式：

均值：（-0.175+0.225+0.325）/3=0.125

方差：[（-0.175-0.125）^2 + (0.225-0.125)^2 + (0.325-0.125)^2 ]/3=0.047

 

 

 

 

 

1.75=1.475+0.275