GBDT原理
| 样本编号 | 花萼长度(cm) | 花萼宽度(cm) | 花瓣长度(cm) | 花瓣宽度 | 花的种类 |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | 山鸢尾 |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | 山鸢尾 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 | 杂色鸢尾 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 | 杂色鸢尾 |
| 5 | 6.3 | 3.3 | 6.0 | 2.5 | 维吉尼亚鸢尾 |
| 6 | 5.8 | 2.7 | 5.1 | 1.9 | 维吉尼亚鸢尾 |
6个样本的三分类问题:
(1)三维向量标志样本的label:
[1,0,0] 表示样本属于山鸢尾,
[0,1,0] 表示样本属于杂色鸢尾,
[0,0,1] 表示属于维吉尼亚鸢尾
(2) 对每一个类训练一个CART Tree 模型: 三个树相互独立
山鸢尾类别训练一个 CART Tree 1。
杂色鸢尾训练一个 CART Tree 2 。
维吉尼亚鸢尾训练一个CART Tree 3
(3) 以样本1为例
针对CART Tree 1,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,1]
针对CART Tree 2,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
针对CART Tree 3,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
(4)CART Tree1生成:哪个特征最合适? 这个特征的什么特征值作为切分点?以CART Tree 1为例
1. 从这四个特征中找一个特征做为CART Tree1 的节点,遍历所有的可能值
1.1 第一个特征【长度】的第一个特征值【5.1cm】为例。
R1 为所有样本中花萼长度小于 5.1 cm 的样本集合,
R2 为所有样本当中花萼长度大于等于 5.1cm 的样本集合。

y1为R1样本的label均值:y1=1/1=1
y2为R2样本的label均值:y2=(1+0+0+0+0)/5=0.2
样本1属于R2的值为:(1-0.2)^2
样本2属于R1的值为:(1-1)^2
样本3属于R2的值为(0-0.2)^2
样本4属于R2的值为(0-0.2)^2
样本5属于R2的值为(0-0.2)^2
样本6属于R2的值为(0-0.2)^2
CART Tree 1在第一个特征【长度】的第一个特征值【5.1cm】的损失值为:(1-0.2)^2+ (1-1)^2 + (0-0.2)^2+(0-0.2)^2+(0-0.2)^2 +(0-0.2)^2= 0.84
1.2 第一个特征【长度】的第二个特征值【4.9cm】计算,损失值为:2.244189
1.3 遍历所有特征的特征值,查找最小的特征及特征值,特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8
2. 预测函数
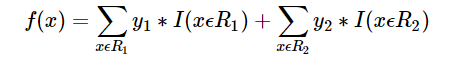
R1 = {2},R2 = {1,3,4,5,6},y1 = 1,y2 = 0.2
样本属于类别山鸢尾类别的预测值f1(x)=1+0.2∗5=2f1(x)=1+0.2∗5=2
同理我们可以得到对样本属于类别2,3的预测值f2(x)f2(x),f3(x)f3(x).样本属于类别1的概率 即为
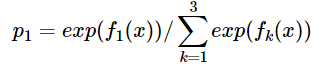
posted on 2018-11-27 17:39 happygril3 阅读(150) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号