贝叶斯推断之最大后验概率(MAP)

本文详细记录贝叶斯后验概率分布的数学原理，基于贝叶斯后验概率实现一个二分类问题，谈谈我对贝叶斯推断的理解。

1. 二分类问题

给定N个样本的数据集，用 $X$ 来表示，每个样本 $x_n$ 有两个属性，最终属于某个分类 $t$

$t=\left\{0,1\right\}$

$\mathbf{x_n}=\begin{pmatrix}x_{n1} \\ x_{n2} \\ \end{pmatrix}$ ，假设模型参数 $w=\begin{pmatrix} w_1 \\ w_2\end{pmatrix}$

$\mathbf{X}=\begin{bmatrix} x_1^T \\ x_2^T \\. \\. \\ x_n^T\end{bmatrix}$

将样本集用用图画出来如下：

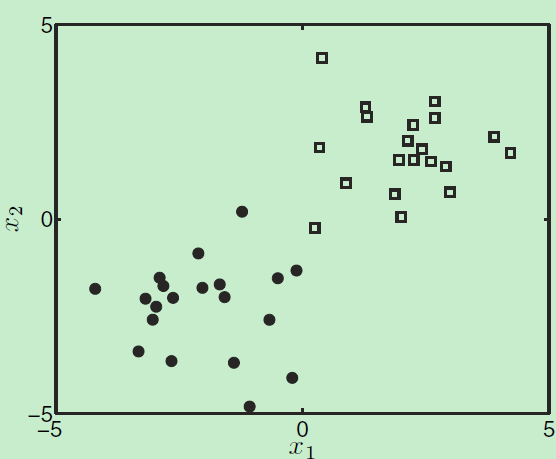
根据贝叶斯公式有：

p (w | t, X) = \frac{p (t | X, w) p (w)}{p (t | X)}

$p(w|t,X)=\frac {p(t|X,w)p(w)} {p(t|X)}$

(公式1)

$p(w | t,X)$ 告诉我们：在已知训练样本集 $X$ 以及这些样本的某个分类 $t$ (这是一个监督学习，因为我们已经有了样本集 $X$ 、以及样本集中每个样本所属的分类 $t$ )，需要求解模型参数 $w$ 。因此， $w$ 是未知的，是需要根据样本通过贝叶斯概率公式来进行求解的。求得了 $p(w|t,X)$ 的分布，也就知道了模型参数 $w$

当我们求得了最优的模型参数之后，给定一个待预测的样本根据公式 $P(T_{new}=1|x_{new}, w^*)$ 来计算新样本 $\mathbf{x_{new}}$ 归类为 1 的概率是多少，这就是模型的预测。

公式1 中等号右边一共有三部分， $p(t|X,w)$ 称为似然概率(likelihood)， $p(w)$ 称为先验概率，这两部分一般比较容易求解。最难求解的是分母: $p(t|X)$ 称为边界似然函数(marginal likelihood)。但是幸运的是，边界似然函数与模型参数 $w$ 无关，因此，可以将分母视为关于 $w$ 的一个常量。

在数学上，若先验概率与似然概率共轭，那么后验分布概率 $p(w|t, X)$ 与先验概率服从相同的分布。比如说：先验概率服从Beta分布，似然概率服从二项分布，这时先验概率分布与似然概率分布共轭了，那么后验概率也服从Beta分布。

因此，在使用贝叶斯公式时，如果选择的先验概率分布与似然概率分布共轭，那后验概率分布就很容易计算出来了（或者说是能够准确地计算出一个 **具体的/精确的 **模型参数 $w^*$ ），这就是：can compute posterior analytically。但现实是，它们二者之间不共轭，从而出现了三种常用的近似计算方法：

点估计(Point Estimate--MAP方法)
拉普拉斯近似方法(Laplace approximation)
采样法(Sampling--Metropolis-Hastings)

而本文只介绍点估计法。

回到公式1，首先来看先验概率，先验概率类似于在做一个决定时，已有的经验。因为我们已经有了训练样本，将这些样本对应的等高线画出来，它们根高斯分布很接近，那么就可以认为先验概率服从高斯分布。也即 $p(w)=N(0,\sigma^2I)$ 。其中， $w$ 是一个向量， $I$ 是单位矩阵。

接下来是似然概率 $p(t|X,w)$ ，假设在给定模型参数 $w$ 以及样本集 $X$ 的条件下，各个样本的分类结果是相互独立的，因此：

$p(t|X,w)=\prod_{n=1}^N p(t_n|x_n, w)$ (公式2)

举个例子，在已知模型参数

w

$w$ 时，

w

$w$ 将

x_{1}

$x_1$ 预测为正类，将

x_{2}

$x_2$ 预测为负类……将

x_{n}

$x_n$ 预测正类，模型对各个样本的预测结果是相互独立的。即：

w

$w$ 对

x_{1}

$x_1$ 的预测结果不会影响它对

x_{2}

$x_2$ 的预测结果。

由于，是二分类问题， ,可以进一步将公式2 写成： $p(t|X,w)=\prod_{n=1}^N p(T_n=t_n|x_n, w)$ ，其中 $T_n$ 代表样本 $x_n$ 被归为某个类的随机变量， $t_n$ 是该随机变量的取值。比如 $t_n=0$ 表示样本 $x_n$ 被分类为正类， $t_n=1$ 表示被归为负类。

2. sigmod函数

由于随机变量取某个值的概率在[0,1]之间，因此要求解 $p(t|X,w)$ ，我们的目标是：找一个函数 $f(\mathbf{x_n};w)$ 这个函数能够产生一个概率值。为了简化讨论，选择 $sigmod(w^T*x)$ ，于是：

$P(T_n=1|x_n,w)=\frac{1}{1+exp(-w^T*x_n)}$

那么：

$P(T_n=0|x_n,w)=1-P(T_n=1|x_n,w)=\frac{exp(-w^T*x_n)}{1+exp(-w^T*x_n)}$

将上面两个公式合二为一：

$P(T_n=t_n|x_n,w)=P(T_n=1|x_n,w)^{t_n}P(T_n=0|x_n,w)^{1-t_n}$

对于N个样本，公式2可写成：

$p(t|X,w)=\prod_{n=1}^N (\frac{1}{1+exp(-w^T*x_n)})^{t_n}(\frac{exp(-w^T*x_n)}{1+exp(-w^T*x_n)})^{1-t_n}$$ **(公式3)**$

至此，先验概率服从高斯分布，似然概率由公式3 给出，就可以求解前面提到的后验概率公式： $p(w|X,t,\sigma^2)$

只要求得了后验概率，就可以使用如下公式计算新样本分为负类的概率：

$P(t_{new}=1|x_{new}, X, t)=E_{p(w|X,t,\sigma^2)}\left(\frac{1}{1+exp(-w^T*x_{new})}\right)$

解释一下这个公式：因为现在已经求得了后验概率

p (w | X, t, σ^{2})

$p(w|X,t,\sigma^2)$ 的表达式，它是一个关于

f (x_{n}; w)

$f(x_n;w)$ 的函数，计算这个函数的期望值

E

$E$ ，这个期望值就是预测新样本

x_{n e w} = 1

$x_{new}=1$ 的概率。

好，接下来就是求解后验概率了。

3. 求解后验概率

前面已经说过，先验概率服从高斯分布 $N(0,\sigma^2I)$ ，似然分布由 公式3 给出，而分母--边界似然函数是一个关于 $w$ 的常数，因此定义一个函数 $g(w;X,t,\sigma^2)=p(t|X,w)p(w|\sigma^2)$ ，函数 $g$ 显然与后验概率 $p(w|X,t,\sigma^2)$ 成比例。因此，求得了函数 $g$ 的最大值，就相当于求得了后验概率的最优参数 $w^*$ 。

这里有个问题就是：凭什么能最大化函数g呢？ $g$ 是 $w$ 的函数， $w$ 取哪个值时函数 $g$ 达到最大值呢？

这里需要用到一个方法叫做牛顿法(Newton-Raphson method)。牛顿法可用于寻找函数中的零点。它通过下面公式：

$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

不断迭代，最终找到函数值为0的点。

而在数学中判断函数在某个点取极值时，有如下定理：

以一元可导函数 $h(x)$ 为例， $h(x)$ 导数为0的点是极值点，但是这个极值点是极小值，还是极大值呢？这时可通过判断 $h(x)$ 是二阶导数来判断该极值点到底是极小值还是极大值。若 $h'(x_n)=0$ 且 $h''(x_n)<0$ ，则，则 $h(x)$ 在在 $x_n$ 处取极大值。

因此，若能够判断 $g(w;X,t,\sigma^2)$ 关于 $w$ 的二阶导数小于0，那么就可以使用牛顿法来求解 $g(w;X,t,\sigma^2)$ 的一阶导数关于 $w$ 的零点，即 $g'(w;X,t,\sigma^2)=0$ 时 $w$ 的取值为 $w_0$ ，这个 $w_0$ 就是最优解 $w^*$ 了。

好，那下面就来证明一下 $g(w;X,t,\sigma^2)$ 关于 $w$ 的二阶导数是小于0的。由于 $w$ 是向量，在多元函数中，相当于要证明的是： $g(w;X,t,\sigma^2)$ 关于 $w$ 的黑塞矩阵是负定的。

将函数 $g$ 取对数，最大化 $log (g(w;X,t,\sigma^2))$ ：

$log (g(w;X,t,\sigma^2))=log({p(t|X,w)p(w|\sigma^2}))$

= l o g (p (t | X, w) + l o g (p (w | σ^{2})

$=log(p(t|X,w)+log(p(w|\sigma^2)$

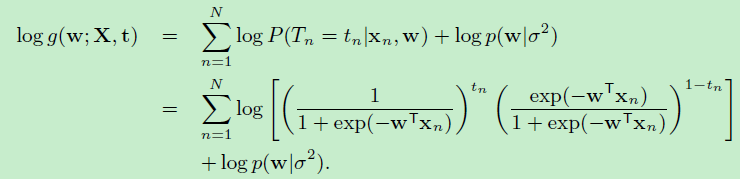
为了简化公式，做如下约定：

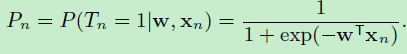
假设 $w$ 是一个 $D$ 维向量：

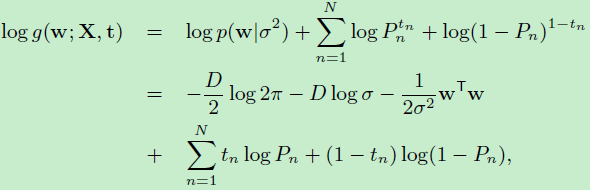
前面三项是先验分布服从高斯分布后，化简得到的结果。根据向量求导公式： $\frac{\partial w^Tw}{\partial w}=w$

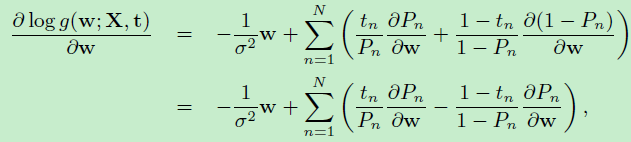
由链式求导法则：

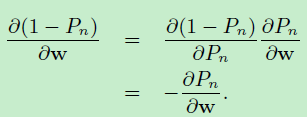
得到：

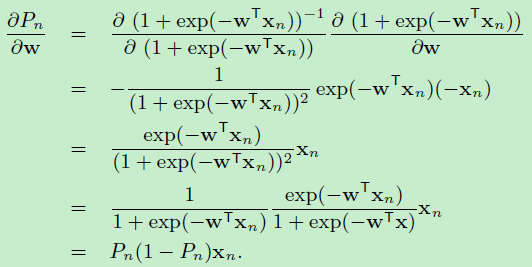
于是： $log (g(w;X,t,\sigma^2))$ 对 $w$ 的一阶偏数如下：

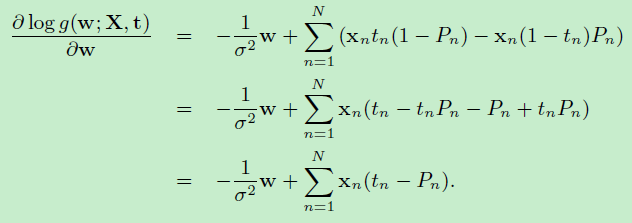
二阶偏导数如下：

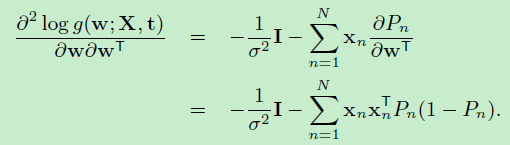
$I$ 是单位矩阵， $0=<P_n<=1$ 是概率值，求得的二阶偏导数就是黑塞矩阵，它是负定的。

证明完毕。

至此，就可以放心地用牛顿法不断迭代，找出 $g(w;X,t,\sigma^2)$ 取最大值时参数 $w$ 的值了，而这个值就是 $w^*$

现在， $w^*$ 求出来了，就可以用下面公式预测新样本 $x_{new}$ 被预测为负类( $T_{new}$ 取值为1)的概率了

P (T_{n e w} = 1 | x_{n e w}, w^{*}) = \frac{1}{1 + e x p (- w^{* T} x_{n e w})}

$P(T_{new}=1|x_{new},w^*)=\frac{1}{1+exp(-w^{*T}x_{new})}$

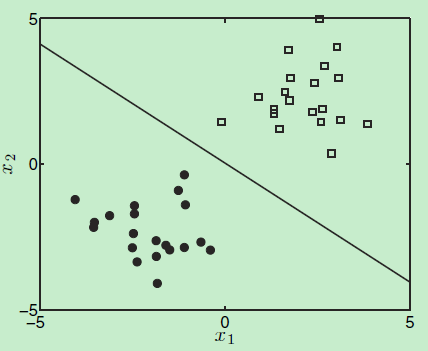
decision boundary

由于是个二分类问题，来看看使用贝叶斯后验概率进行分类的决定边界长什么样子。由于输出的是一个概率值，显然约定 $P(T_{new}=1|x_{new},w^*)>0.5$ 预测为负类， $P(T_{new}=1|x_{new},w^*)<0.5$ 时预测为正类。那等于0.5时呢？

根据：$$P(T_{new}=1|x_{new},w^{*)=\frac{1}{1+exp(-w}x_{new})}=0.5$$得出：

$-w^{*T}*x=0=w_1^*x_1+w_2^*x_2$

$x_2=\frac{w_1^*}{w_2^*}*(-x_1)$

也就是说样本 $\mathbf{x}=\begin{pmatrix}x_{1} \\ x_{2} \\ \end{pmatrix}$ 的两个属性 $x_1$ 和 $x_2$ 是成线性比例的。而这条直线就是decision boundary

总结

贝叶斯方法是机器学习中常用的一种方法，在贝叶斯公式中有三部分，先验概率分布函数、似然概率分布函数、和边界似然概率分布函数（贝叶斯公式的分母）。求出了这三部分，就求得了后验概率分布，然后对于一个新样本 $x_{new}$ 计算后验概率分布的期望值，这个期望值就是贝叶斯模型的预测结果。

由于后验概率分布的计算依赖于先验概率分布函数、似然概率分布函数，当这二者共轭时，后验概率与先验概率服从相同的分布函数，从而可以推导计算出后验概率分布(posterior could be computed analytically)。但是，当这二者不共轭时，则是计算后验概率分布的近似值。计算近似值一共有三种方法，点估计法(point estimate --- MAP)，拉普拉斯近似法，Metropolis-Hastings采样法。而本文主要介绍是第一种方法：点估计法(point estimate --- maximum a posteriori)。

maximum a posteriori中的最大化体现在哪里呢？其实是体现在似然分布函数的最大化上。黑塞矩阵的负定性证明了 $g(w;X,t,\sigma^2)$ 有最大值，再使用牛顿法不断迭代找到了这个使得函数 $g$ 取最大值的最优参数解 $w^*$ 。而求得了最优参数 $w^*$ ，就求得了后验概率分布公式。对于一个待预测的新样本 $x_{new}$ ，计算该样本后验概率分布的期望值，这个期望值就是贝叶斯模型对新样本的预测结果。