[Note]WQS 二分

[Note]WQS 二分

Preface:
感觉大部分网上的总结都说得不太清楚，以下是我自己的理解。@2025/04/15

已大幅度修订@2025/05/07

添加 Part 4 @2025/05/08

Part 1. 普通 WQS 二分

我们经常遇到下列问题：

给定若干个物品，要求恰好选择 \(k\) 个，且代价最大/最小

这类问题的一般做法是把 \(k\) 设为 DP 中的一个维度，不过这样会多一个 \(\mathcal O(n)\) 的复杂度。我们即将说明，如果答案函数 \(f(n)\) ，表示恰好取 \(n\) 个物品的时候答案为 \(f(n)\)，且其满足关于 \(n\) 的函数是凸的，那么有一个可以用 \(\log n\) 的时间将这个问题转化成其不限制个数的版本，只要这个问题能够在 \(\mathcal O(T(n))\) 的时间内解决，那么原问题就可以在 \(\mathcal O(T(n)\log n)\) 的时间内解决。

我们以该函数上凸为例：

我们知道，上凸函数的斜率是单调递减的，在这个问题中，以线段 \(DE\) 为例，其斜率意味着从 \(D\) 点横坐标（即 \(f(4)\)）转移到 \(f(5)\) 时进行的最优决策的收益。这个决策可能是从原先最优的方案里面拿出来一些物品，然后放进去一些物品。而我们现在能够快速求解的问题是，求解这个凸壳的最大值点，就是最顶上的点的坐标 \((x,f(x))\)。

以下我们假设当前要求 \(f(4)\)

所以我们考虑，要把前者转化成容易解决的后者，我们就需要对凸壳进行一定变换，将我们的目标 \((k,f(k))\) 换到最上面去。容易想到，我们把凸壳的每一个边的斜率减掉 \(x\)，就能更改凸壳的最大值点，而要想把 \(D(4,f(4))\) 换到顶上去，就要减去 \(\operatorname{slope}(CD)\)。凸壳的性质保证了我们这样做之后它还是一个凸壳。如图：

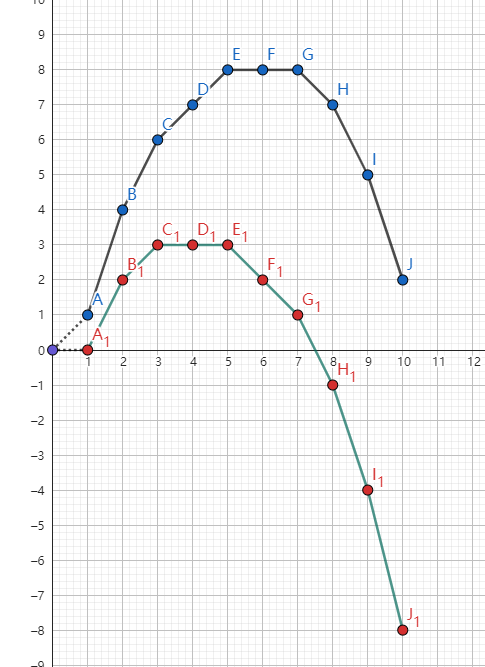
绿色折线即变换后的凸壳，此时用不限个数的算法即可求解最高点 \(D(4,f(4))\)。看到了吗，\(CD\) 被拉平了。每个点 \((x,f(x))\) 的纵坐标都减去了 \(x\operatorname{slope}(CD)\)。方便起见，我们把 \((0,0)\) 作为 \(f(0)\) 加入。

这就是其他教程讲的添加惩罚系数或者二分斜线斜率切凸包的含义。在直接求解的过程中算法有选择最优的那个的功能，施加一个惩罚系数，可以阻止算法选择过少或者过多物品，为什么可以用这种简单的方法完成，因为图像有特殊的凸性，以上分析过程就是原因。

我们又知道，上凸壳的斜率是单调不增的，我们可尝试二分这个减去的斜率 \(x\)，如果算出来的横坐标比目标小，意味着 \(x\) 应该小一点，否则就应该大一点。

我们再来看看减去斜率这个操作的实际意义，其实就是将每一个物品的代价减去了 \(x\)，然后就可以执行不限个数的算法了。

Part 2. 例题 最小度限制生成树

给你一个有 \(n\) 个节点，\(m\) 条边的带权无向图，你需要求得一个生成树，使边权总和最小，且满足编号为 \(s\) 的节点正好连了 \(k\) 条边。

P5633 最小度限制生成树 - 洛谷

遇到“恰好”的限制我们可以考虑 wqs 二分，首先就要判定答案函数 \(f(x)\) 的凸性

上凸：\(F(x)-F(x-1)\ge F(x+1)-F(x)\)

下凸：\(F(x)-F(x-1)\le F(x+1)-F(x)\)

引理 答案函数 \(f(x)\) 是下凸的

引理 1 答案不为 Impossible 的 \(x\) 是连续的一个区间

比较明显，证明略。

如图，如果这是完全图 \(\{A,B,C,D,E,F,G\}\) 的一个生成树：

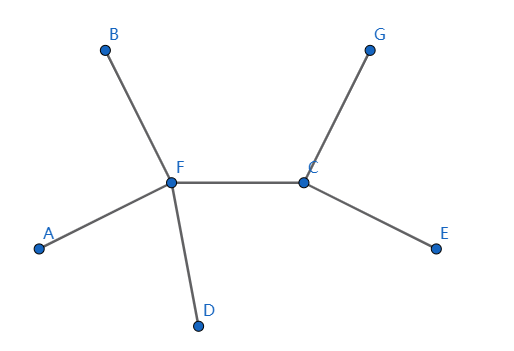
若 \(s=F\)，那么此时它连了 \(4\) 条边，假如就是 \(f(4)\) 对应的最优解。如果添加一条边

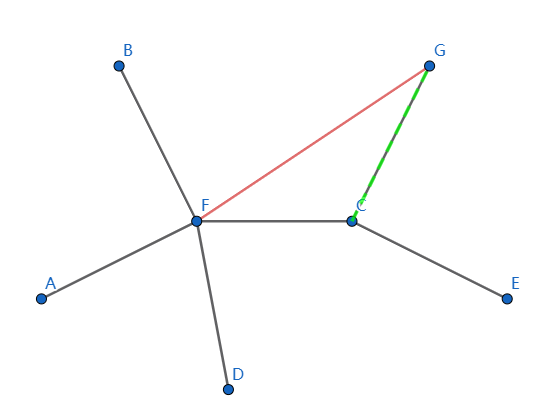
引理 2 在使得点 \(s\) 的度数变大 1 的时候，一定存在一个方案不删掉已经与 \(s\) 连接的边

这是因为，无论是操作之前的局面，还是操作之后的局面，都是最优的。由于添加的边都是与 \(s\) 相连的，假设有一条原来与 $s $ 相连的边被删掉，那么它肯定与新加入的边构成环，设原先的边是 \(x\)，新加入的边是 \(y\)。那么由于原来 \(x\) 在最优方案中，所以必有 \(w(x)\le w(y)\)，然而当前也是最优方案，所以把 \(y\) 用 \(x\) 替换，答案不会变劣。\(\square\)

添加红色边 \(FG\) ，必须去掉一条边，假设是这条绿色的 \(CG\)。鉴于 \(f(4)\) 的最小性，有 \(f(5)\ge f(4)\)。 如果我们考虑再加入一条边，那么新加入的这条边减去它删除的这条边的权值，即 \(f(6)-f(5)\)，也就是答案的变化量，肯定是不小于 \(f(5)-f(4)\) 的，否则在从 \(f(4)\) 转移到 \(f(5)\) 的时候就先加入这条边了。

一般地，我们有 \(f(x)-f(x-1)\le f(x+1)-f(x)\)，那么这个函数是下凸的。\(\square\)

那么，我们可以应用 wqs 二分，配合 Kruskal 算法作为内层来解决这个问题。要注意的是，这个例子里面的物品其实是与 \(s\) 相连的边，所以其实只对这些边的边权有操作，我们把这些边和其他边分开来，每次用归并排序合成一个数组，渐进复杂度可以少一个 \(\log n\) 因子。

注意：求解的时候可能遇到若干边斜率相等的问题，如上面 Part 1 中示例中的 \(C,D,E\) 三个点，此时应仔细考虑内层所用 check 算法返回的横坐标究竟是这一个斜率相等的段中间的哪一个点。

Part 3. 如何输出方案

如果 Part 2 中的问题要求我们输出方案，应该怎么处理呢？CF125E MST Company - 洛谷

你也许认为，Kruskal 算法不是能够求出方案吗？难道不是很简单吗，回顾一下我们之前的例子，\(C,D,E\) 这三个点，我们求最高点的时候，这几个点的答案是相等的，我们并不能保证 Kruskal 能恰好求到 \(x=k\) 的那一组，例如我们要求的是 \(C\) 点所对应的方案。

注意：作者也不确定这个方法的正确性，只知道它没有被上面这种情况 hack 掉。

但是，我们确实可以通过更改排序函数，以边权为第一关键字，以边是否与 \(s\) 连接为第二关键字，我们可以求得这一段的最左边/最右边的那个点。那么，如何构造恰好 \(x=k\) 的方案呢？

我们先求出最左边那个点对应的方案，这个方案中对应的所有与 \(s\) 相连接的边都是在这一段里所有方案中都存在的，我们说这些边是必要的。我们再求出最右边那个点对应的方案，顺便求出 \(g_x\) 表示边权大于 \(x\) 的边中不必要的、能出现在生成树中的、且与 \(s\) 相连的边。

然后再执行一次 Kruskal，若正在考虑一个与 \(s\) 相连的边 \(x\)，若当前已经选的与 \(s\) 相连的边数 \(c\) 加上 \(g_x\) 还不足 \(k\)，那么这个边要选，否则就不选。

wqs 二分求答案的复杂性就在于，内层 check 算法有的的性质并不是那么好，不容易做出这种构造，而且这种构造的通用性似乎非常弱。

Part 4. 例题 以及 如何证明凸性

除了用定义，还能用四边形不等式和费用流来证明凸性。

P4983 忘情

将一个长度为 \(n\) 的正整数序列分成 \(k\) 段，对于每一段，定义其权值为：

\[\left(\frac{\bar{x}\sum_{i=1}^n{x_i}+\bar x}{\bar{x}^2}\right)^2 \]

最小化每一段权值的总和，其中 \(\bar x\) 是该段的平均数，\(n\) 为此段长度。

上式容易化为 \((\sum_{i}x_i+1)^2\)。我们现在就说明，如果 \(f(x)\) 表示分成 \(x\) 段的答案，那么这个函数下凸。

对于正整数序列的任意划分，段数少的权值和不小于段数多的权值和

我们先证明，这个性质对于只有两段的划分是正确的，由于序列任意排序之后这个性质仍然成立，所以可以不管顺序，设总和为 \(n\)，则更强的一个结论是证 \((a+1)^2+(n-a+1)^2\le (n+1)^2\) 成立。

\[\begin{aligned} &(a+1)^2+(n-a+1)^2\le (n+1)^2 \\ \iff & a^2+2a+1+(n-a)^2+2(n-a)+1\le n^2+2n+1 \\ \iff & a^2+2a+1+n^2-2na+a^2+2n-2a+1\le n^2+2n+1\\ \iff & 2a^2-2na+2\le 2n+1\\ \iff & 2a^2-2na-2n+1\le 0\end{aligned} \]

在这里，由于 \(n\ge a\ge 1\)，所以 \(2a^2\ge 2na\)，又 \(n\ge 1\)，所以上式成立。

做出归纳假设，设对于分 \(k\) 段以下的划分都满足这个性质，那么对于分 \(k\) 段的情况，用上述性质合并两段可以归约到 \(k\) 段以下的情况。\(\square\)

好的所以上面这个好像没什么用，有一个经典结论就是用四边形不等式证明，作者懒得写了，参见 四边形不等式优化 - OI Wiki (oi-wiki.org)

CF958E2 Guard Duty (medium) / P3620 [APIO/CTSC2007] 数据备份

给定 \(n\) 个时间点。每个区间都以某两个时间点为左右端点，且每个区间的「代价」定义端点的时间之差。你要选择 \(k\) 个连续的区间，保证这个 \(k\) 个连续的区间没有交集，且代价总和最小。

首先，选择的都一定是排序后相邻的两个。然后本题可以使用费用流做：

这样交错建图，可以发现很明显的退流的意义，就是把一段交错选/不选的区间反转，这就是交错路或者说，增广路的考虑方法吧。通过这个可以导出反悔贪心算法，或者你也可以管他叫（仅在本题中），模拟费用流。

那么，这个与 WQS 二分有什么关系呢？我们知道有一个结论：费用流有凸性，意思是，费用流的最小费用关于总流量有凸性，因此能够用费用流做的这一类问题，都有凸性。所以本题同样有 WQS 二分做法。