省选算法复习

省选算法复习

相比于之前还是有很多更加深入的理解 qwq

1. 线段树优化建图

当我们需要向区间内所有点连边或者从区间中所有点连到某个点的时候，便可以使用线段树来优化，如果需要从区间每一个点连到另一个区间每一个点的话，加一个虚点就好了。

这不是一个很困难的技巧，关键在于要建模。

P5471 [NOI2019] 弹跳 - 洛谷

本题，要求从一个点连接到一个矩形里面的所有点。然后求最短路径。

14-18 号测试点就是模板线段树优化建图。9-13 号测试点是直接建图。1-8 是暴力。

那么 KDT 其实也可以优化建图，但是空间太小了，运气好也许能过 19-22.

只是简单地进行一维技巧的二维扩展好像是比较无效的，因为这种情况下你很难指定第二位应该连哪些边。

现在的问题是要建立的边有 \(\mathcal O(m\sqrt n)\) 条，存不下。

2. KDT

KDT 是维护高维点集的有力结构。其结构保证：点数 \(\mathcal O(n)\) 树高 \(\mathcal O(\log n)\) 矩形查询 \(\mathcal O(\sqrt n),\text{general form }\mathcal O(n^{1-1/k})\)

---

我们可以继续看这个题，qwq

考虑无论边有多少条，能到达的点最多 n 个，而建图的目的就是快速遍历所有能够到达的点。所以不把边建出来即可。

另外，本题也可以不使用 KDT 优化建图，见杂题日推 I，这种方法更巧妙。

---

查询复杂度分析

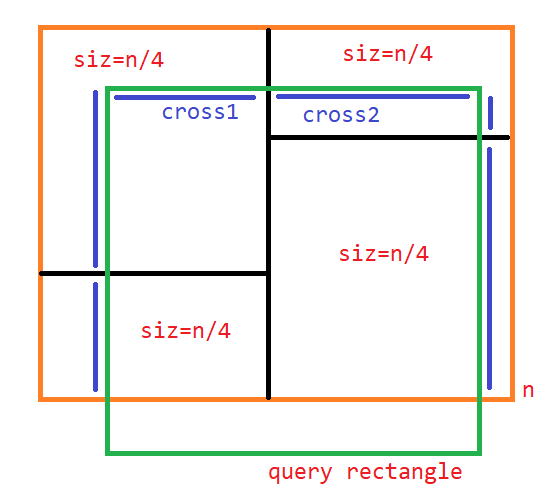
容易知道，一次查询的复杂度就是部分被查询区间包含的节点个数，我们先考虑完全包含查询区间的节点，这至多有 \(\mathcal O(\mathbf{height})=\mathcal O(\log n)\) 个，而不完全包含的，如上图。

对于当前节点，若子树大小为 \(n\)，那么考虑画出它儿子、孙子的划分，上图中每一份的子树大小都是 \(n/4\)，我们可以对查询矩形的每一条边来考虑，发现矩形的一条边至多穿过两个孙子，然后对于每一个被穿过的孙子，递归考虑，可以写出：

\[T(n)=2T(n/4)+\mathcal O(1) \]

由主定理，\(T(n)=\mathcal O(\sqrt n)\)。

插入删除

我们有两种策略

1. 插入/删除的个数超过一定阈值就全局重构，单次修改均摊 \(\mathcal O(n\log n/B)\)，查询均摊 \(\mathcal O(B+n^{1-1/k})\)。

2. 适用于仅有插入的情况，这同样对其他大量不支持插入的数据结构管用，即二进制分组，插入时，新建大小为 1 的某数据结构，然后不断将大小相同的拿来拍平重构。这样，如果最后数据结构有 \(n\) 个点，那么总插入复杂度就是 \(\mathcal O(n\log^2 n)\)。

注意用替罪羊维护是假的。

3. BSGS & exBSGS

经典 BSGS 是用于解决离散对数问题的：

求关于 \(x\) 的同余方程的解 \(a^x\equiv b\pmod m\) 其中 \(a\perp m\)。

我们用一个类似双向搜索的思路。

令 \(x=A\left\lceil\sqrt m\right\rceil-B\)，那么 \(a^x\equiv b\pmod m\) 可以写成 \(a^{A\left\lceil\sqrt m\right\rceil-B}\equiv b\pmod m\) 这可以化为 \(a^{A\left\lceil\sqrt m\right\rceil}\equiv ba^B\pmod m\)。

需要特别注意的是，这一步转化意味着原方程的解是转化后方程的一个解，但是，转化后方程的解不一定是原来方程的解。要使得他们是等价的，就需要 \(a^B\) 在模 \(m\) 下的逆元存在，即 \(a\perp m\)。

枚举 \(B\) 计算方程右边的值，然后枚举左边的值，查找是否存在右边的某个值与之对应。

将特殊的多次剩余问题化为 BSGS 能解决的问题

这类问题的形式是

求关于 \(x\) 的同余方程的解 \(x^a\equiv b\pmod p\) 其中 \(p\) 是质数。

由于模数是质数，那么它一定存在原根 \(g\)，由原根的定义，模 \(p\) 意义下任何数都可以表示为 \(g^i\) 的形式。

那么我们用 \(g^i\) 代换 \(x\) 化为求解 \((g^{a})^i\equiv b\pmod p\) 然后利用 BSGS 求解即可。

扩展 BSGS

这类问题的形式是

求关于 \(x\) 的同余方程的解 \(a^x\equiv b\pmod m\)。

我们尝试将其化为 BSGS 能够处理的问题。

我们遂尝试将方程同时除以 \(d_1=(a,m)\)：

\[\frac{a}{d_1}\times a^{x-1}\equiv \frac{b}{d_1}\pmod{\frac{m}{d_1}} \]

同样地，需要注意的是，我们除掉 \(d_1\)，这个操作确实是一个等价变换（稍后我们可以全部乘以 \(d_1\)），但是如果方程两边同时乘以 \(d_1\)，就有可能不是等价变换了（\(d_1^{-1}\pmod {\frac{m}{d_1}}\)不一定存在）！

如果此时 \(a\not\perp \frac{m}{d_1}\) 那么重复执行上述操作，直到满足 \(a\perp \frac{m}{d_1d_2d_3\dots d_k}\)。由于满足这个条件，所以 \(\frac{a^k}{d_1d_2d_3\dots d_k}\perp \frac{m}{d_1d_2d_3\dots d_k}\)，将这个除到右边去，问题化为普通 BSGS 能够解决的形式。

4. CRT

解方程，就是把方程转化成一个等价的形式，如果转化之后恰好等价，这其实说明这个方程组所含信息量和转化之后的是一样的，如果转化之后有增根，说明不是完全的等价变换，如果转化之后根不全，说明原先方程含的信息还多一些。这里我们非常感性地说“信息量”，但是我们也可以用线性代数的严谨语言去替换它。所以如果我们要做到不漏掉解也不多解的话，我们就要对方程进行步步等价的变形。

这一点，我们在以后再探讨。

中国剩余定理是解决以下问题的：

\[\left\{\begin{aligned} &x\equiv a_1\pmod{n_1}\\ &x\equiv a_2\pmod{n_2}\\ &\vdots\\ &x\equiv a_k\pmod{n_k} \end{aligned}\right. \]

其中 \(n_1,n_2,\dots,n_k\) 两两互质，求解上面的方程组。

以下令 \(A=\prod a_i,M=\prod n_i\)

有一个构造，就是

\[x\equiv \sum a_i\frac{M}{n_i}{\left(\frac{M}{n_i}\right)^{-1}\bmod{n_i}}\pmod {M} \]

有点奇妙，因为右边这项恰在模 \(n_i\) 的时候其他的被除掉，这一项被抵消掉，因为中间的逆元是模 \(n_i\) 意义下的逆元。容易知道，满足上述条件的同余方程组有且仅有上面一个解（当然是模 \(M\) 意义下的）。

没有互质的一般情况

考虑只有两个方程的情况，转化为不定方程问题来解决，这个转化是等价转化，exgcd 解决即可。

5. 最小斯坦纳树

斯坦纳树解决这样的问题，在连通图上有若干关键点，求一个原图的子图使得这些关键点都连通，且子图中边权总和最小。

显然，子图的形状一定是一棵树。这个问题看起来就是动态规划能够解决的，因为我们发现一棵树的不重不漏的生成方式可以是：

• 加点

• 子树拼接

其实考虑答案的生成方式就是在考虑遍历状态空间，而无论是什么问题，计算机解决它的基本思路大多都是用某种方式遍历状态空间。这样的思路在符号化方法中也可以见到。

那么这里我们选择子树拼接方法，我们设 \(f_{S,i}\) 其中 \(S\) 为一个点集合，\(i\in S\) 为这个点集的树根，那么转移即：\(f_{S,i}=\min_{T\subsetneq S,p\in T,q\in S\setminus T}\left\{f_{T,p}+f_{S\setminus T,q}+w(p,q)\right\}\)

这种方式，复杂度是 \(\mathcal O(n^23^k)\)，跑不满，在大部分题目是够用的，思路也相当简单。

我们发现一个奇怪的地方，那就是 \(f_{S,i}\) 的转移与 \(i\) 没有关系，所以我们其实可以省略它，但是复杂度没有变化。

现在复杂度的瓶颈主要就是枚举两个点集中的点，这其实是求一个点集到另一个点集的最短距离。我们把 \(i\) 的定义换成任意一个点，相当于我们提前处理了 \(S\) 到另外一个点的最短距离，此时我们转移就变成 \(f_{S,i}\gets f_{S,j}+w(i,j)\) 和 \(f_{S,i}\gets f_{T,i}+f_{S\setminus T,i}\)。而第一项转移是等于最短路，我们对于每一个 \(S\) 做一次最短路即可。

6. 树上启发式合并

树上启发式合并是一类小巧好用的思想，用来求解静态的子树统计信息，要求统计的复杂度是与子树大小有关的。我们从子树得到父亲的答案时，直接继承重儿子的信息，暴力计算其他儿子的子树即可。证明略，考虑每一个点被计算的次数是 \(\mathcal O(\log n)\) 的。

7. FFT 与 NTT

在 OI 中，FFT 将多项式转化为在复数单位根或者原根的次幂处的点值表示。值得注意的是，复数单位根和原根都是对应群的生成元。

算法的基本思路就是将多项式按照奇偶次数分开，然后合并，根据这两种生成元的对称性合并答案，减少一半的计算。这或许意味着多项式具有在某种意义上的对称重复的结构。