信息学总结[寒假集训]
寒假总结
FBI Warning:本文只是写给自己备忘的,作者是蒟蒻,有各种错误轻喷
0. 前面的
关于0x00,一些基础的东西,我已经进行了总结,见luogu blog
其他比较重要的东西,比如ST、倍增,我并不比lyd总结的好,还是看书把。
0x01的单调栈,也曾进行了总结。
1. 起点:字符串Hash P67 0x14
字符串hash是一种将字符串映射成一个非负整数的方法,便于参与运算,其发生hash冲突的概率极端小。一个字符串的hash值就几乎可以唯一代表这个字符串。它还支持一些运算性质,从而我们可以进行判等、判子串等操作。
但是,不能用hash值进行大小比较之类的操作(废话)。
常用实现方法:
取值P,将字符串看作P进制数(所以P一定要能囊括整个字符集)。
再取一模数M,求该P进制数对M取模的值作为字符串的Hash。
一般取P=131或13331,取\(M=2^{64}\)。并不进行取模运算,当unsigned long long类型溢出时,相当于自动对M取模。
其余对字符串的操作就可转换成对该P进制数的操作。
2. 字符串和基础数据结构 P70 0x15
2.1 KMP模式匹配
KMP模式匹配是能够高效找出文本串T中与模式串M相等的字串的出现位置。
它的基本优化思想是跳过不可能的无用位置,直接跳到下一个可能处继续匹配,从而减少徒劳的匹配时间。
它的如何选择失配时的下一个位置呢?
考虑暴力算法,当发现不匹配时,暴力算法要放弃当前方案,推进一位后重新匹配。
考虑暴力算法过程中已经计算了的部分,我们已经知道这一部分与字符串中的一部分相等。于是我们选择原字符串中这一段:前缀和真后缀相等的长度i,并令当前匹配长度为这个长度i,相当于我们已经从这个位置匹配了i个,跳过了一步步向前推进模式串的过程。
关于更加详细的实现,请看Link
2.2 最小表示法
见P76,讲的很好。基础思想跟KMP差不多,也是及时排除不可能位置。
2.3 Tire
实现见P77
实际上,他也是排除不可能选项,再每一个字符位置上及时排除其他字符。
你可以在节点上存储额外信息来达到一些目的。
其实,他也不是只能处理字符串,还能处理二进制拆分之类的。
2.4 二叉堆
二叉堆将数据组织到一棵完全二叉树上,使得插入/删除时不必要重新进行整个序列的排序。
-> 应用:霍夫曼树
3. 搜索
搜索算法是计算机解决问题的基本方法
对问题进行求解,实际上是在问题空间对应的状态空间中进行映射和遍历
大部分的算法都是对搜索、暴力的优化。
3.1 树和图基础
书P93
这里不讲,只是附一张有意思的图
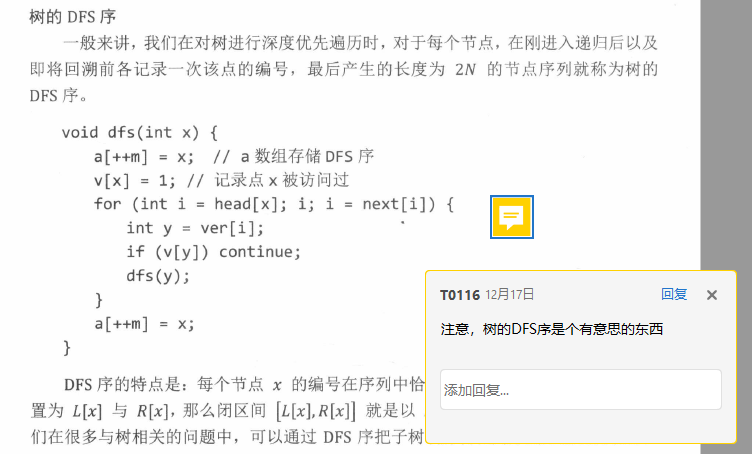

3.2 广搜与拓扑排序
广度优先搜索已经在上面的luogu博客里讲过,不在赘述
那么拓扑排序是什么呢?

所以,我认为,拓扑序是某种程度上的节点重要性排序,也就是说,删除拓扑序中的某一个节点,有可能会导致无法从原先入度为0的点访问到后面的节点,但是肯定不会影响前面的节点。
3.3 搜索剪枝
搜索剪枝,是一种剪除搜索树上不必要枝条的手段,通过及时避免不可能产生答案的遍历来优化搜索运行的时间复杂度。
剪枝是有多种实现方案的,我从我常用的角度进行了排序:
- 最优性剪枝
如果当前代价花费已经大于已经搜到的答案,那么直接剪枝
- 可行性剪枝
如果当前方案不可行,剪枝
- 记忆化
记录每个状态的搜索结果,若重复遍历一个状态就直接返回结果。
或者,在某些问题中,如果无法更新状态的答案(即当前代价不优于记录的代价),就直接剪枝。
- 排除等效冗余
- 优化搜索顺序
3.4 迭代加深与双向搜索
迭代加深和双向搜索都是避免DFS在深层子树中浪费时间的方法,其实也可以用于BFS,而且在BFS中的应用比在DFS中更加广泛。
粘个图

3.5 广搜变形
- 双端队列、优先队列BFS
其实,普通的BFS可以解决走地图问题中每一步代价都一样的那种问题
但假如代价不一样了呢?
这时候,我们就可以使用双端或优先队列,来进一步区分权值(贪心地)。
例题: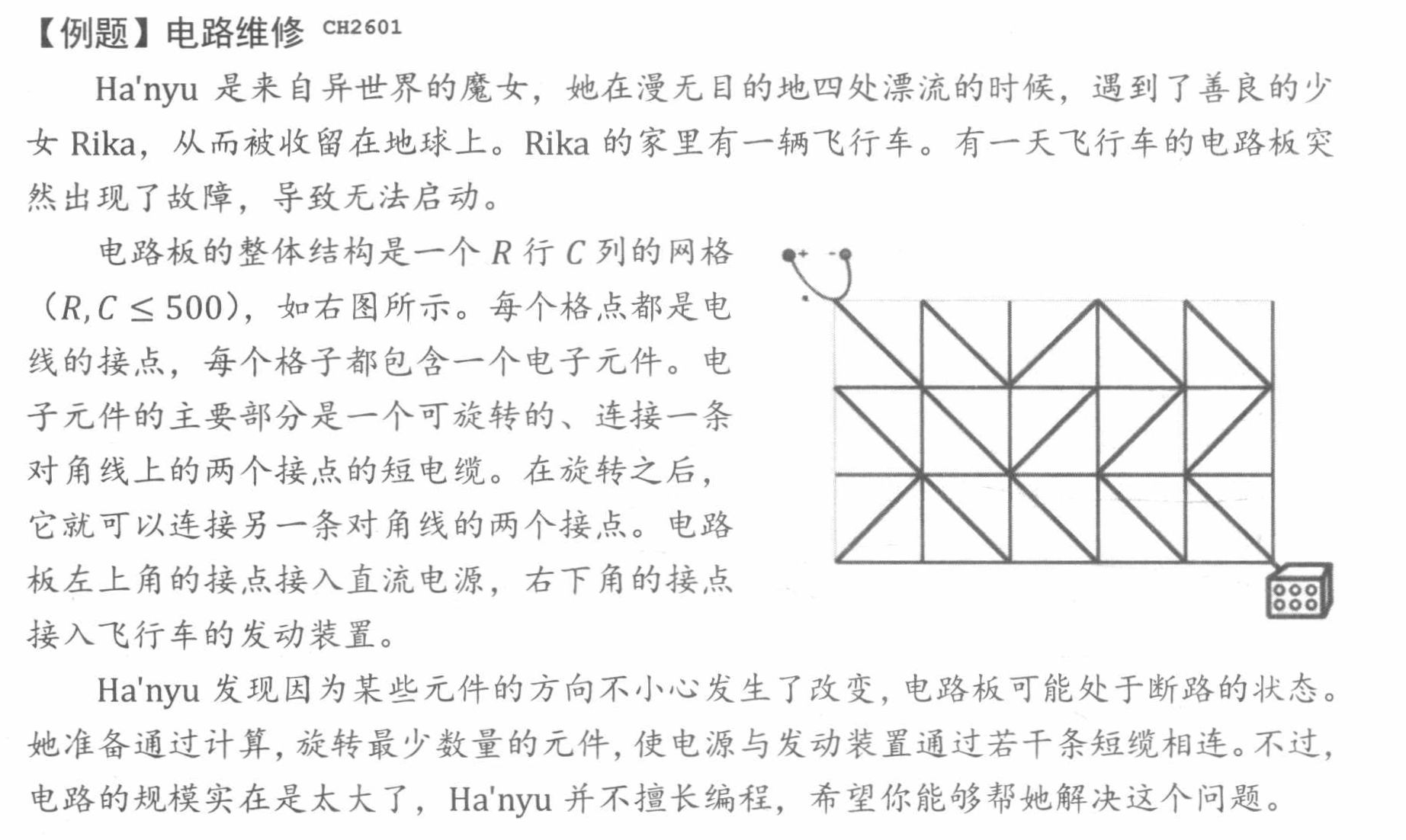
在这题中,如果扩展方向是联通的,那么不费代价,否则要费1的代价。
实际上,优先队列BFS求最短路问题,就是堆优化的Dij
3.6 A&IDA

其实,A*就是多想一步,尽可能早地找到最优解,看起来就像是优化了搜索顺序一样。
同样的,IDA*只是把BFS换成了DFS,并对每次状态还需要的递归步数进行估计,若当前已经走的步数加上估计超过限制就回溯。
3.7 总结
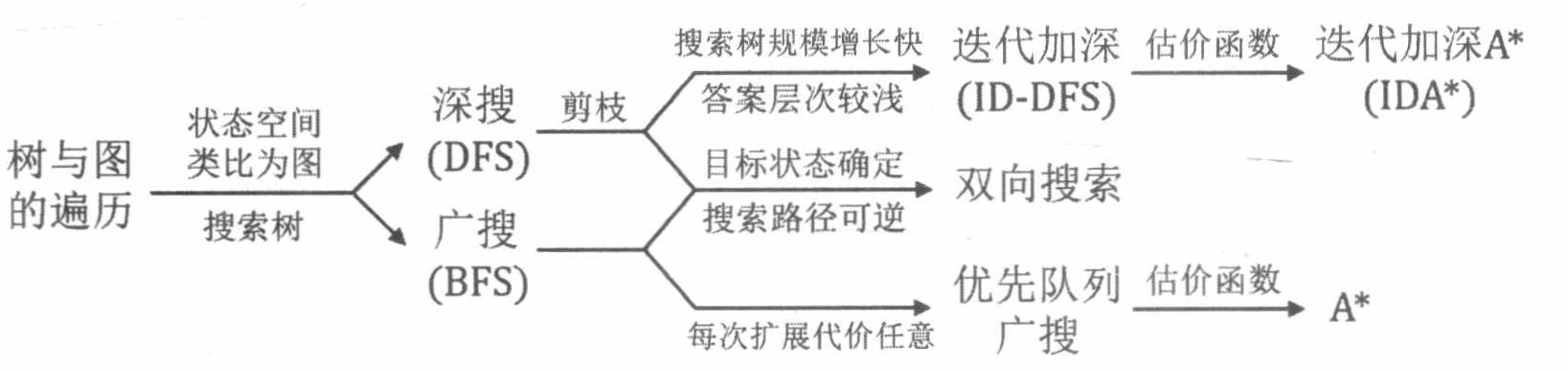
4. 进阶数据结构
4.1 并查集
并查集是一种可以动态维护若干个不重叠的集合,并支持合并与查询的数据结构。
采用代表元法,即为每个集合选择一个固定的元素,作为整个集合的代表
已经总结过,戳Link
并查集更擅长维护添加关系,对于删除可以倒着维护。
并查集并不关心并查集的树结构,为提高效率,可以丢弃它们。
4.2 树状数组
树状数组,是通过对区间进行二进制划分,在保证可以取到任意一个区间的前提下,对前缀和信息进行大段维护和访问的一种数据结构。
通过划分数据,来达到前缀和查询复杂度和修改复杂度的平衡。
由于二进制划分的性质,按照访问层序依次从上往下询问和从下往上修改。

图中,红色路径显示了add(5)的路径,黑色路径显示了ask(14)的路径
其中,我们发现ask、add经过的路径恰好是一位一位地减少或增多末尾的一,所以我们用lowbit运算处理刚好
由于是维护前缀和,我们可以通过存储差分数组来进行区间修改(区间查询也可以)
4.3 线段树
给数据区间分成左右两边,在对一整段进行操作时直接对大区间进行操作,并且在递归时只用递归其中一边。(实际上,似乎3进制划分比2进制划分好一点,这是因为3比2更接近e(大雾)
线段树维护的信息一定是需要满足区间可加性的,这是为了方便将左右两边合成大区间。
关于线段树的其他的动态开点之类的,见P220
线段树十分通用,它也很重要,但是思想是比较简单的。
比较重要的其实是比较复杂的打标记和下传,这个都是因题而异的,大家可以去看看 [SHOI2015] 脑洞治疗仪
4.4 分块和莫队
分块算法通过将数据分块,对于区间操作,做到大段维护,局部朴素的维护。所以,我们又可以把它总结为暴力+暴力=分块
实际上,在前面的树状数组和线段树,都是通过不同的分块方式,对数据操作进行优化。
这里有一个对比图: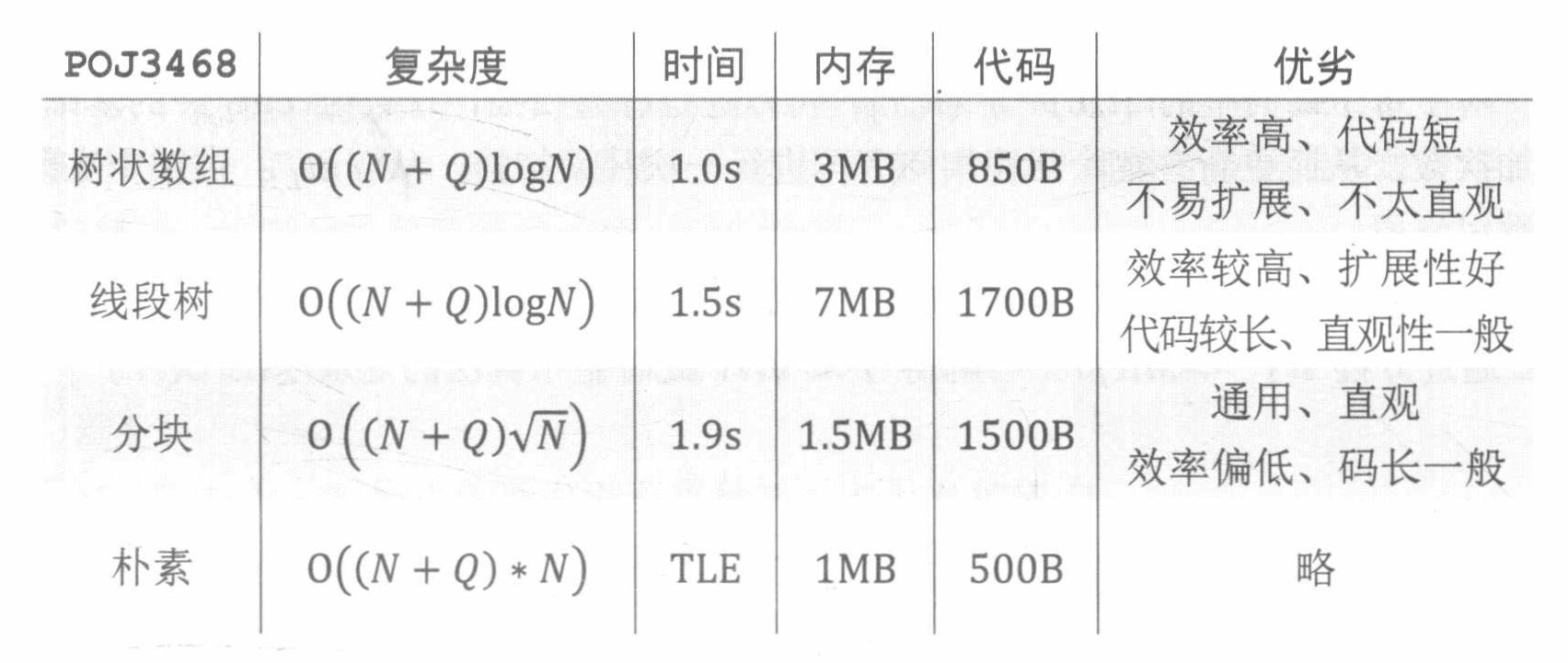
块长通常是取\(O(\log N)\)
莫队,实际上是一种排序询问的策略,就是以分块进行询问的分类,再通过块外块内排序,使得询问尽量靠近,接着我们朴素处理询问变化的那些数据,得到一个个询问的答案。
由于需要对询问进行排序,所以该算法是离线的。
但是一个问题通常不会只有询问,还会有修改操作,这时候怎么办呢?
我们可以给莫队升一个时间维,用来表示当前操作是在什么时候进行的,以便我们可以控制更新的位置。
4.5 平衡树
- BST
BST,通过划分关键码来划分数据,这样在查询时就只需要访问一边。
在数据关键码随机的情况下它的期望复杂度就是\(O(\log N)\)。但是BST很容易退化,如果插入一个有序序列,它的复杂度就变成了\(O(n)\)
其实,写到这里,已经可以感受到什么是数据结构的精髓了:
数据结构就是,以某种方法划分信息,使得在操作时容易排除不可能的选项,达到排除不可能或做到时空平衡
所以,为了解决退化问题,以下将BST转换为一棵比较平衡的树的方法,就是平衡树。
- Treap
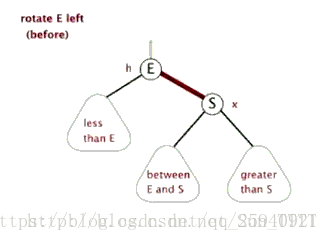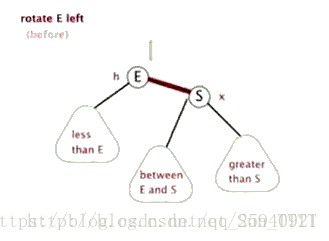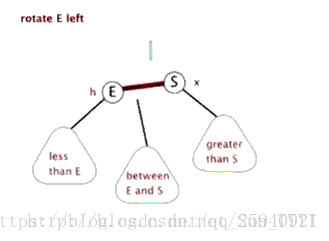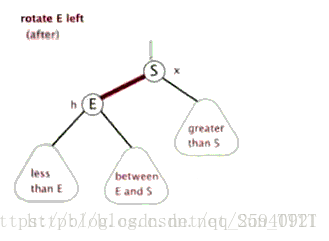
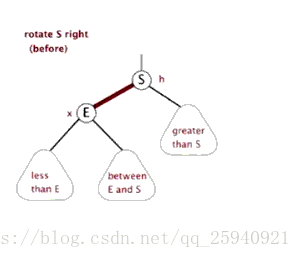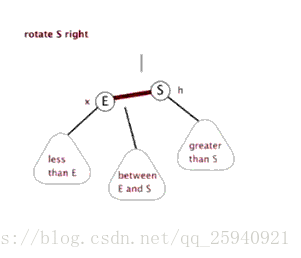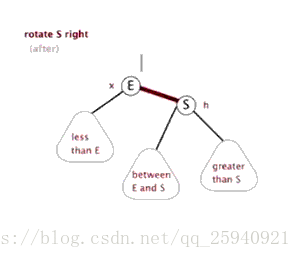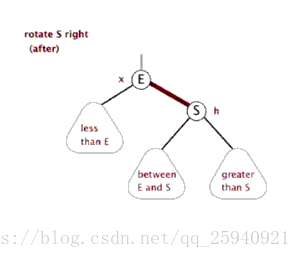
(Zag同理) 注意,上图有问题,Zig是Pushup(rs(p)),即结束时更新原来p,q对应点的值
Treap,是Heap和Tree这两个单词的合成,这说明了Treap维持树平衡的方法———利用堆性质。
关于它的实现之类的,网上的教程大多数已经把它扒的干干净净了,这里只讲讲它的时间复杂度的一个问题:
对于堆来说,他是完全二叉树的意义在哪里呢?就是保证,树的深度一是\(O(\log N)\)的。
那么,对于Treap,这一样吗?不一样。他首先要保证正确性,肯定是优先要满足BST性质,这个情况下再满足堆性质,所以,一棵Treap不一定是像堆那样的完全二叉树,所以是肯定不是像堆那样完全保证复杂度是\(O(\log N)\)。Treap的优先级是随机赋予的,由于随机数是分布均匀的,才有可能复杂度期望是\(O(\log N)\),
我觉得这里有一篇博客解释这个问题解释的很不错:
我们在BST中讲过,普通的BST具有很强的不确定性,如果数据特殊,建树的时候可能直接变成一条链。不仅如此,插入删除的时候也很麻烦。因为如果插入或者删除,整个树原来的结构就会被打乱,这会为遍历和查找带来灾难性的后果。
所以我们推出了平衡树。就是通过将树旋转来动态维护这个树形态是平衡的,这样查找的复杂度就是O(log)级别的,是一种稳定的复杂度。
树堆是一种平衡树,它通过为键值(也就是我们需要维护成BST的)赋予优先级,使之也满足堆结构来进行旋转,成为一棵平衡树。
但是我们需要注意一点:树堆的优先级是随机赋予的。也就是说,这个数据结构其实是一个随机化的数据结构。这不是树堆的缺点,因为只有随机化赋予优先级,才有可能保证树堆的复杂度是O(log)的级别。
那么,上述性质也说明了,树堆并不是一个规则形态的二叉树,更不是堆需要满足的完全二叉树。甚至它也不符合平衡树的定义:每个节点左右子树高度相差≤1,所以我们说树堆是近似实现平衡。
但是通过形态定义二叉树的方式并不绝对。我们换一种方式来对平衡树进行定义:
能够保证时间复杂度的BST,就是平衡树。
- FHQ-Treap
FHQ-Treap是Treap的另一种实现形式,不通过旋转来保持平衡,而是通过分裂-合并操作过程中保持平衡,因为他的分裂操作,可以方便地取出想要操作的子树。
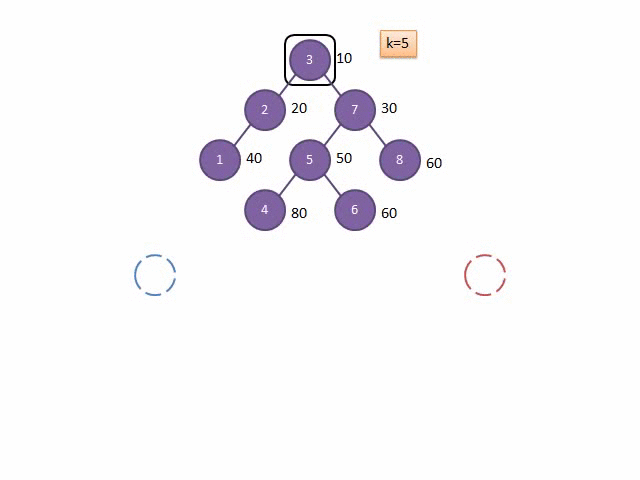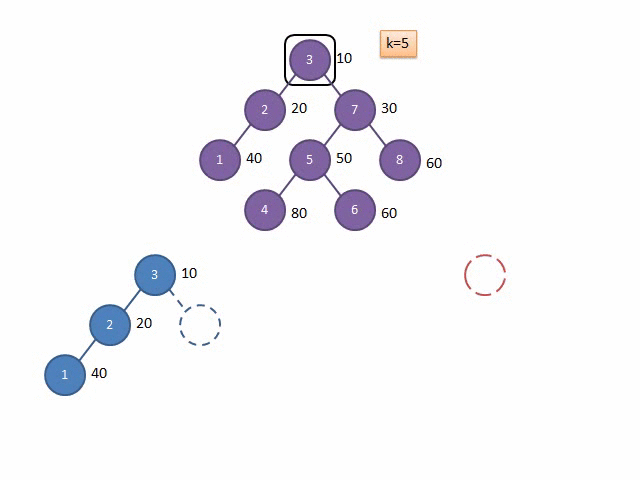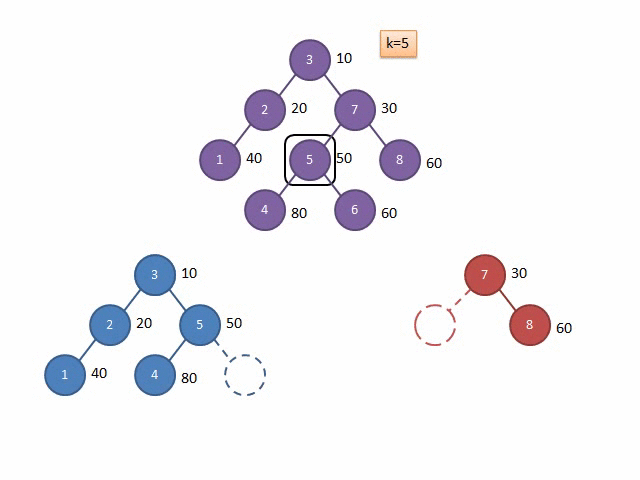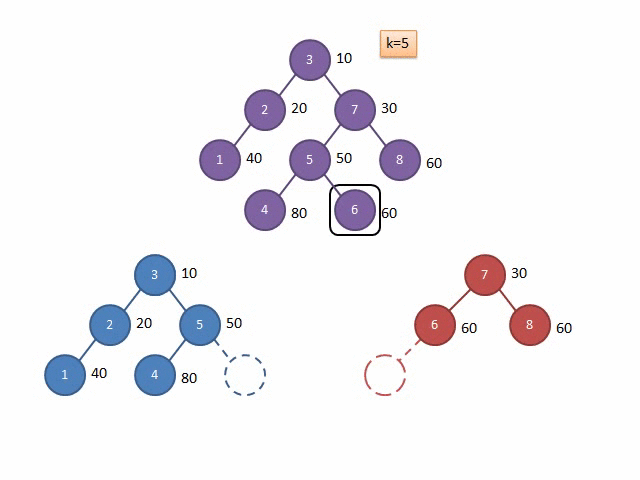
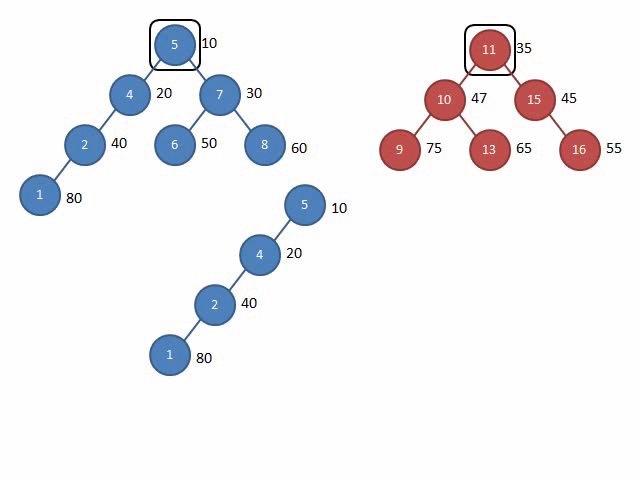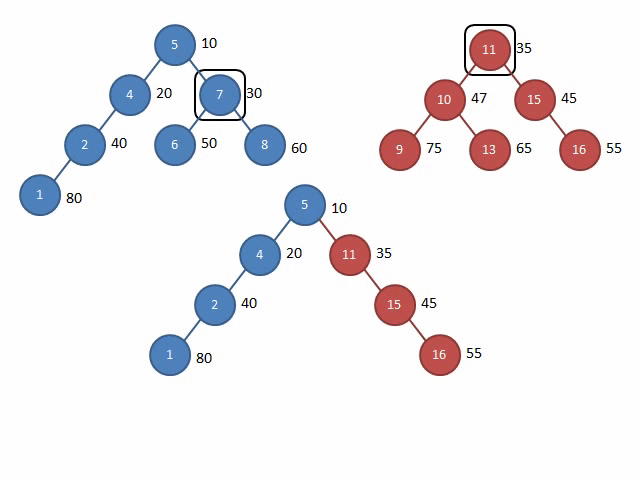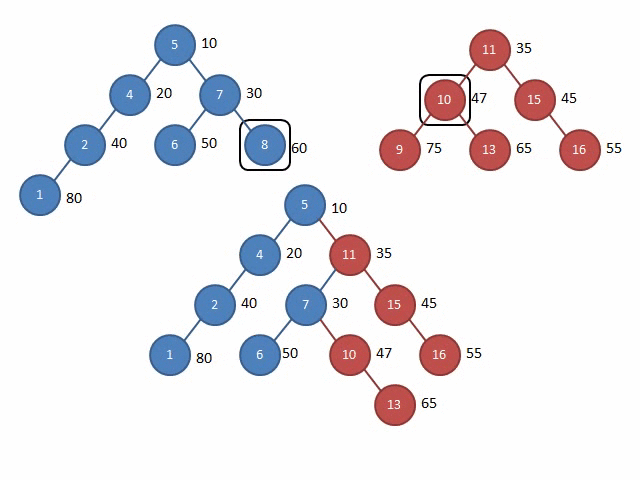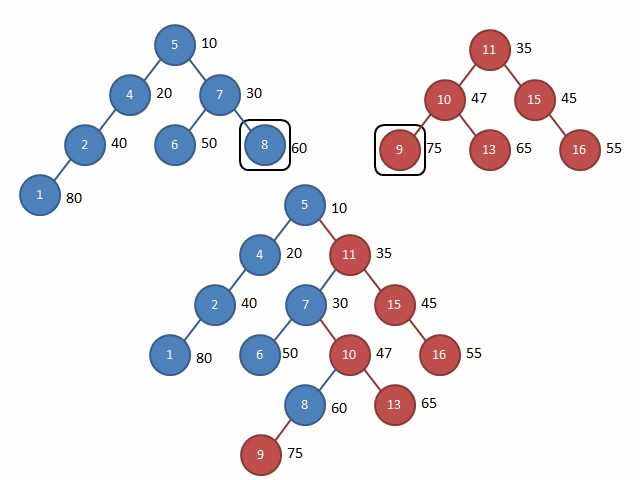
这里放两张Gif解释一下Split和Merge的过程:
图源:远航休息栈 - FHQ-Treap
Split
Merge
注意,这个Merge的图有点问题,但是大致过程就是这样,具体详见图源的评论区。
其他的操作,都可以通过按大小分裂或按权值分裂找到操作位置再合并,就十分简单了,同时,也可以选择在节点上存储额外信息来达到其他目的(例题:文艺平衡树)。
具体的可以看OI-wiki(蓝皮书上没有)
- 其他
还有笛卡尔树、替罪羊树这些,不是十分重要,就不专门记录了。
4.6 点分治和CDQ分治
太难了,还是看书把。
4.7 可持久化数据结构
可持久化原意是保存数据集的历史版本,但是如果真的一个个复制,不仅时间开销大,空间更是无法接受。所以,我们只新建被修改的部分,重用之前的节点。
- 可持久化线段树
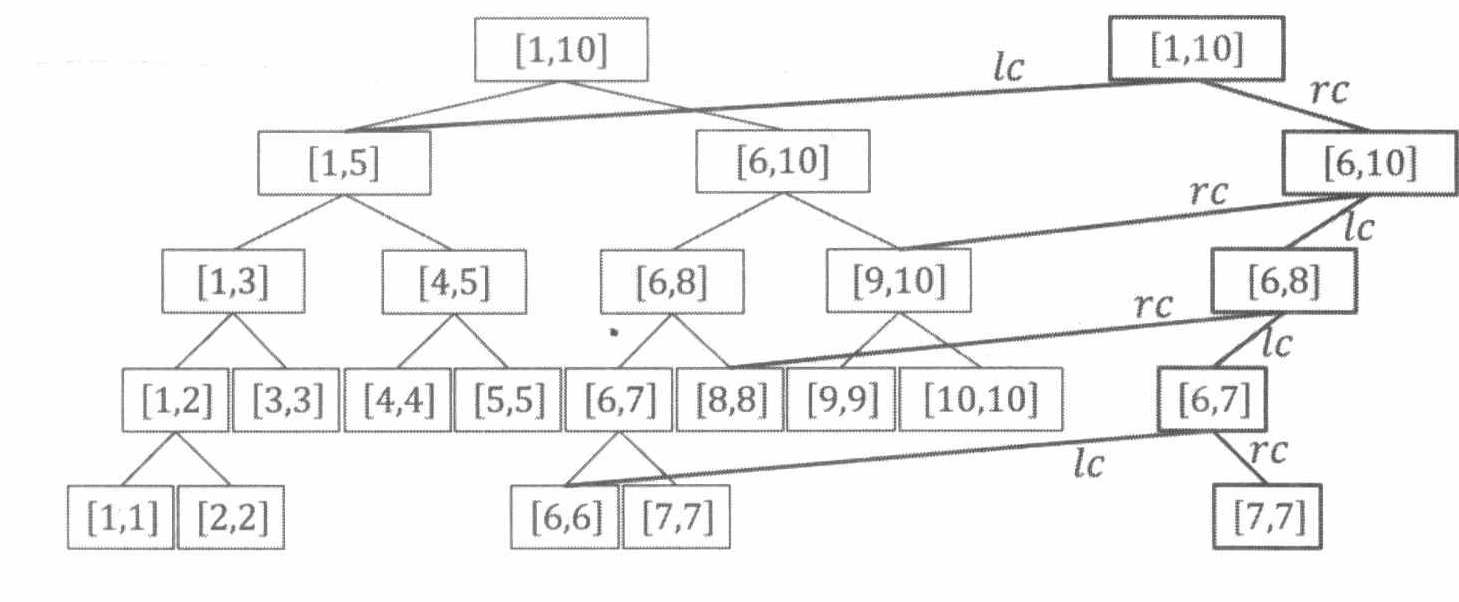
- 可持久化Tire
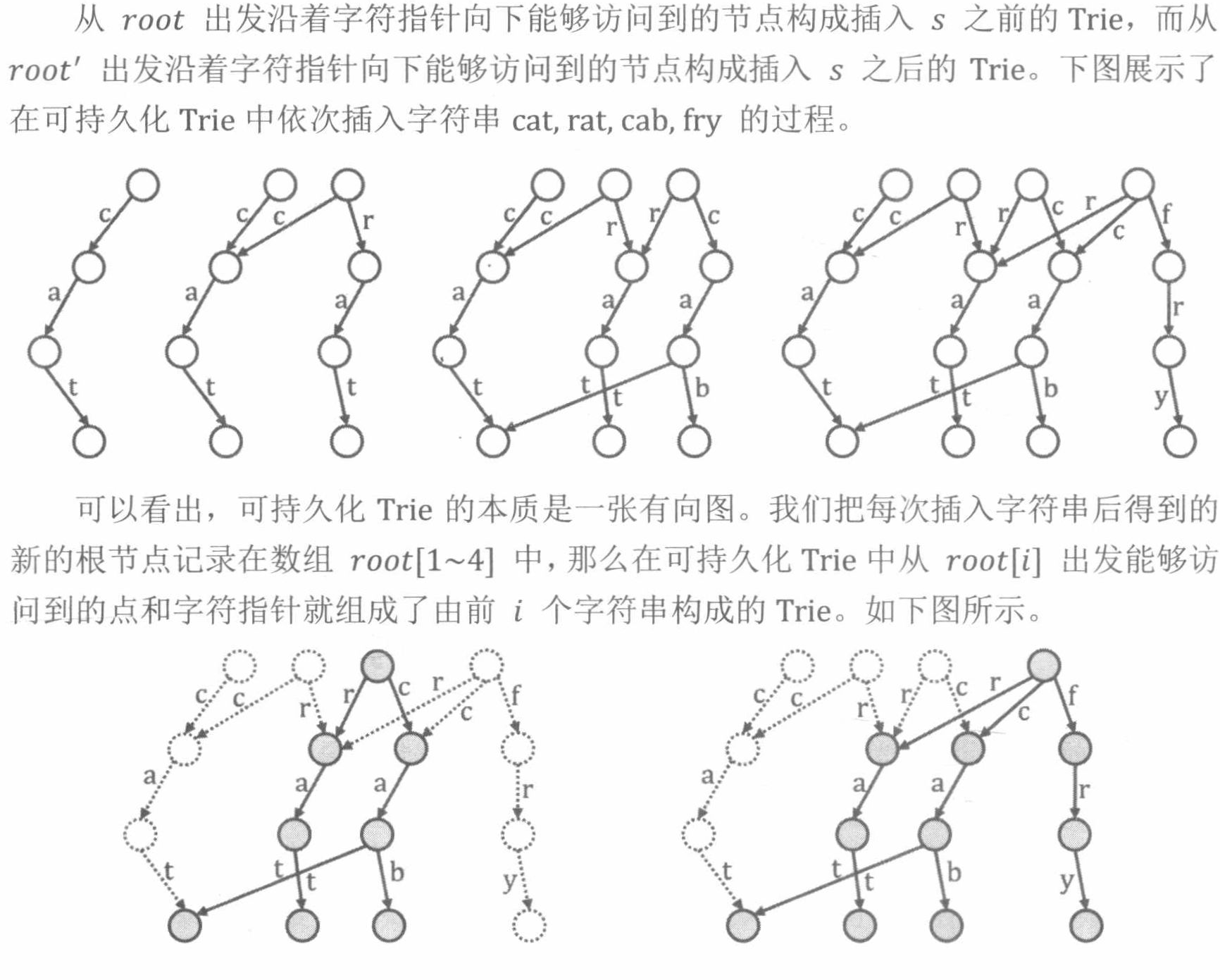
本文来自博客园,作者:haozexu,转载请注明原文链接:https://www.cnblogs.com/haozexu/p/17153703.html





 浙公网安备 33010602011771号
浙公网安备 33010602011771号