背包问题

01背包

集合思想解决01背包问题

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int v[N], w[N], f[N][N];
int n, v;

int main()
{
    cin >> n >> v;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= v; j ++) {
            f[i][j] = f[i-1][j];
            if (j > w[i]) f[i][j] = max(f[i][j], f[i-1][j-w[i]] + v[i]);
        }

    cout << f[n][v];

    return 0;
}

完全背包问题

有 \(N\)种物品和一个容量是 \(V\) 的背包，每种物品都有无限件可用。
第 \(i\) 种物品的体积是 \(v_i\)，价值是 \(w_i\)。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

问题分析

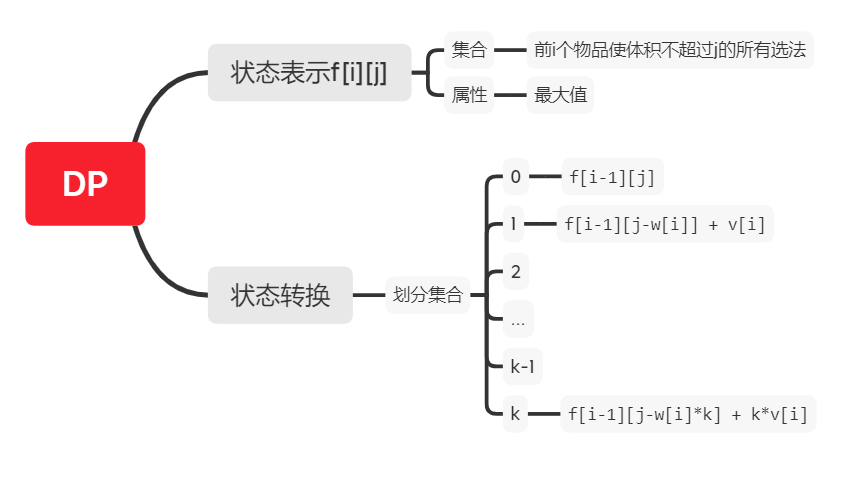
三重循环做法

#include<iostream>
using namespace std;

const int N = 1010;
int v[N], w[N], f[N][N];
int n, m;

int main ()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> w[i] >> v[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j ++)
            for (int k = 0; k * w[i] <= j; k ++) {
                f[i][j] = max(f[i][j], f[i-1][j-k*w[i]] + k*v[i]);
            }

    cout << f[n][m];

    return 0;
}

优化到二重循环

f[i,j]=max(f[i,j],f[i-1,j-w[i]]+v,f[i-1,j-2w[i]]+2v...f[i-1,j-kw[i]]+kv)
f[i,j-w[i]]=max(  f[i-1,j-w[i]],  f[i-1,j-2w[i]]+ v...f[i-1,j-kw[i]]+(k-1)v)

由上可以将2式中的部分替换到一式中得到

f[i][j] = max(f[i][j], f[i][j-w[i]] + v[i])

完整代码如下：

#include<iostream>
using namespace std;

const int N = 1010;
int v[N], w[N], f[N][N];
int n, m;

int main ()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> w[i] >> v[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j ++) {
            f[i][j] = f[i-1][j];
            if (j >= w[i]) f[i][j] = max(f[i][j], f[i][j-w[i]] + v[i]);
        }
                
    cout << f[n][m];

    return 0;
}

多重背包问题

有 \(N\)种物品和一个容量是 \(V\) 的背包
第 \(i\) 种物体最多有\(s_i\)件其体积是 \(v_i\)，价值是 \(w_i\)。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。
\(0<N,V≤100\)
\(0<v_i,w_i,s_i≤100\)

与完全背包问题十分详细重点在于优化部分先给出暴力解法

暴力解法（朴素做法）

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 210;
int n, m;
int v[N], w[N], s[N], f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> w[i] >> v[i] >> s[i];

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
            for (int k = 0; k <= s[i] && k*w[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i-1][j-k*w[i]] + k*v[i]);

    cout << f[n][m];

    return 0;
}

二进制优化

​ 分析原来暴力做法的时间复杂度\(O(NVS)\)对于之前所给的数据范围是可以在\(1s\)之内完成计算的但对于数据范围为\(0<N≤1000, 0<V≤2000, 0<v_i,w_i,s_i≤2000\) 的时候需要运行\(10^9\)显然会超时。

​ 我们可以将对于前\(i\)个物品每个物品最多选\(s\)个，将\(s\)个物品进行划分划分成\(1,2,4,8,16,...\)组每个组只有选或者不选两种这样就可以把前i个物品每个物品最多选s个这种情况全部描述出来

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 15000, M = 2020;
int w[N], v[N], f[N];
int n, m;

int main()
{
    cin >> n >> m;
    int cnt = 0;
    for (int i = 1; i <= n; i ++) {
        int a, b, s;
        cin >> a >> b >> s;

        int k = 1;
        while (k <= s) {
            cnt ++;
            w[cnt] = a * k;
            v[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0) {
            cnt ++;
            w[cnt] = a * s;
            v[cnt] = b * s;
        }
    }
    n = cnt;

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= w[i]; j --)
            f[j] = max(f[j], f[j-w[i]] + v[i]);
    
    cout << f[m];

    return 0;
}