JAVA有关位运算的全套梳理
一、在计算机中数据是如何进行计算的?
1.1:java中的byte型数据取值范围
我们最开始学习java的时候知道,byte类型的数据占了8个bit位,每个位上或0或1,左边第一位表示符号位,符号位如果为1表示负数,为0则表示正数,因此要推算byte的取值范围,只需要让数值位每一位上都等于1即可。
我们来用我们的常规思维来分析下byte类型的取值范围:
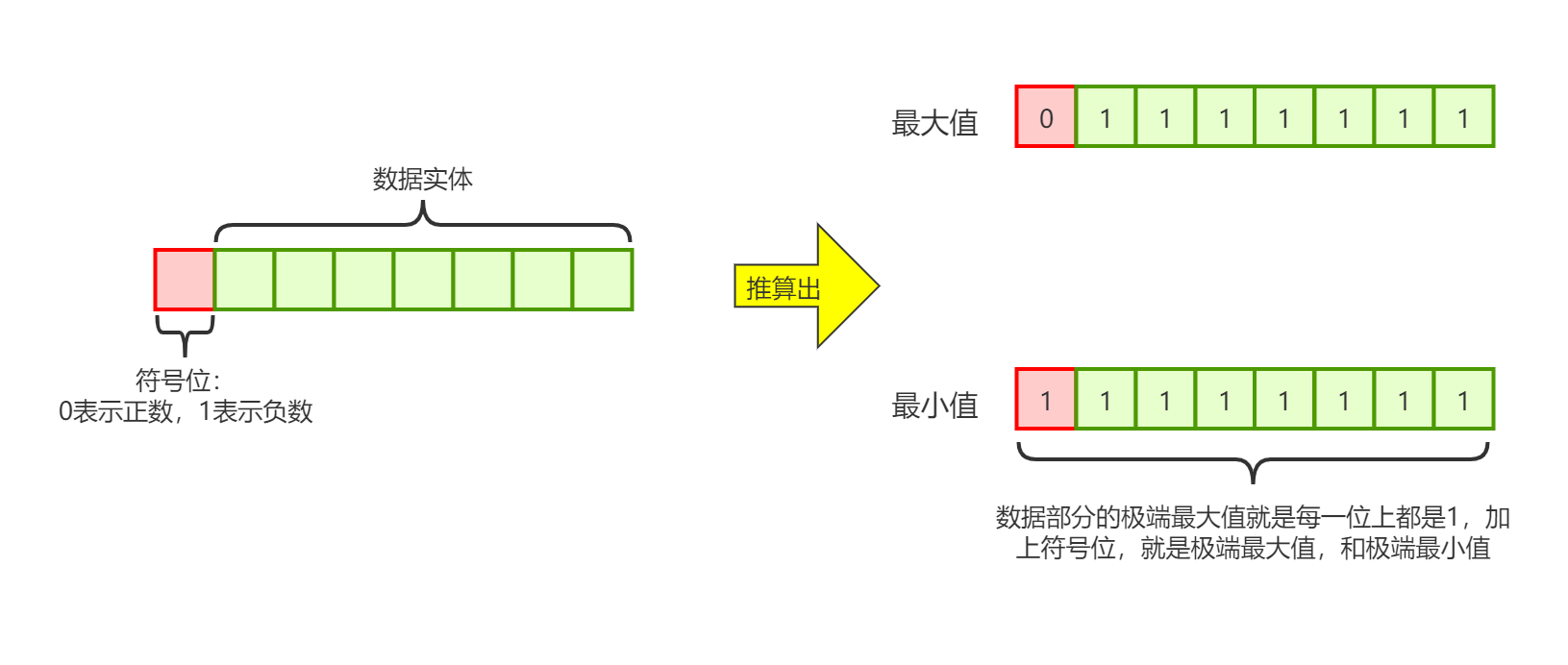
图1
如果按照这种思路来推算,七个1的二进制数转换为十进制是127,算上符号位,取值范围应为:-127~+127,但事实上我们知道,byte的取值范围是-128~127,这里先打个问号,接着往下看。
现在让我们计算下byte类型的7加上byte类型的-2是多少:
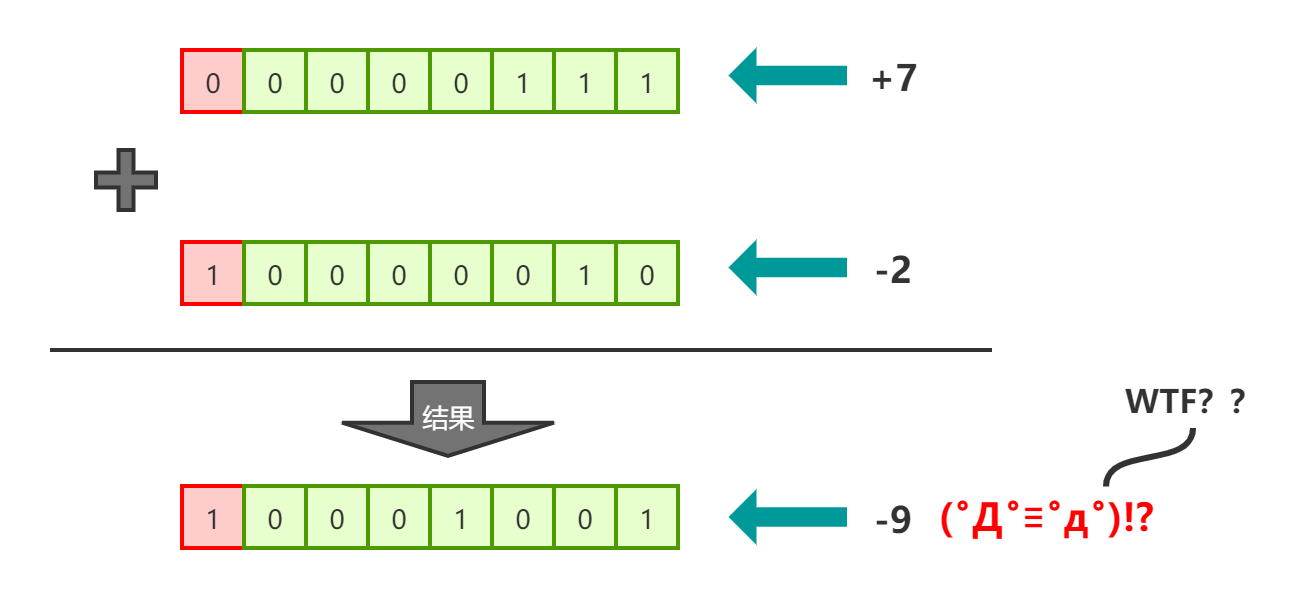
图2
诶?跟我们预想的不一样,因为我们是知道7和-2的和应该是5才对,结果应该表示为:00000101,但事实上通过图2的结果来看确实跟预想的不一样,所以计算机在做计算的时候,肯定不是表面上的符号位+数值位的方式进行的计算的。
1.2:原码,反码,补码
我们先来看下定义:
👉 原码定义:符号位加后面的数值,比如图2里的00000111和10000010都是原码,原码比较简单,就是我们在上面单纯理解上的原值。
👉 反码定义:正数的反码就是它的原码,负数的反码符号位不变,其余数值位全部按位取反,例如:
00000111的反码:00000111
10000010的反码:11111101
👉 补码定义:同样的,正数的补码仍然等于它的原码本身,负数的补码等于它自己的反码+1,例如:
00000111的补码:00000111
10000010的补码:11111110
🌴 总结:正数的原码、反码、补码完全一致,负数的反码等于它原码的数值位按位取反,负数的补码等于它的反码+1
现在让我们用反码的方式来计算下图2中的式子:
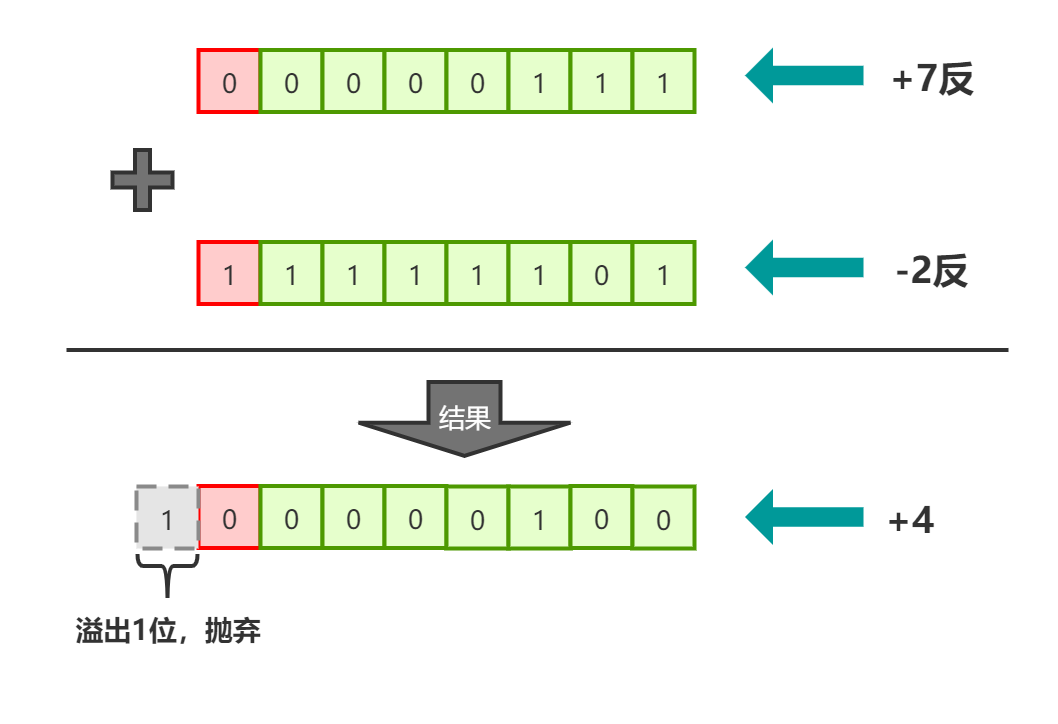
图3
利用数值的反码计算出的结果已经很接近正确答案了,+4的反码等于它的原码,现在只需要让它+1就是正确答案,还记得补码的定义吗?负数的补码等于它的反码+1,那现在让我们用补码做下计算试试?
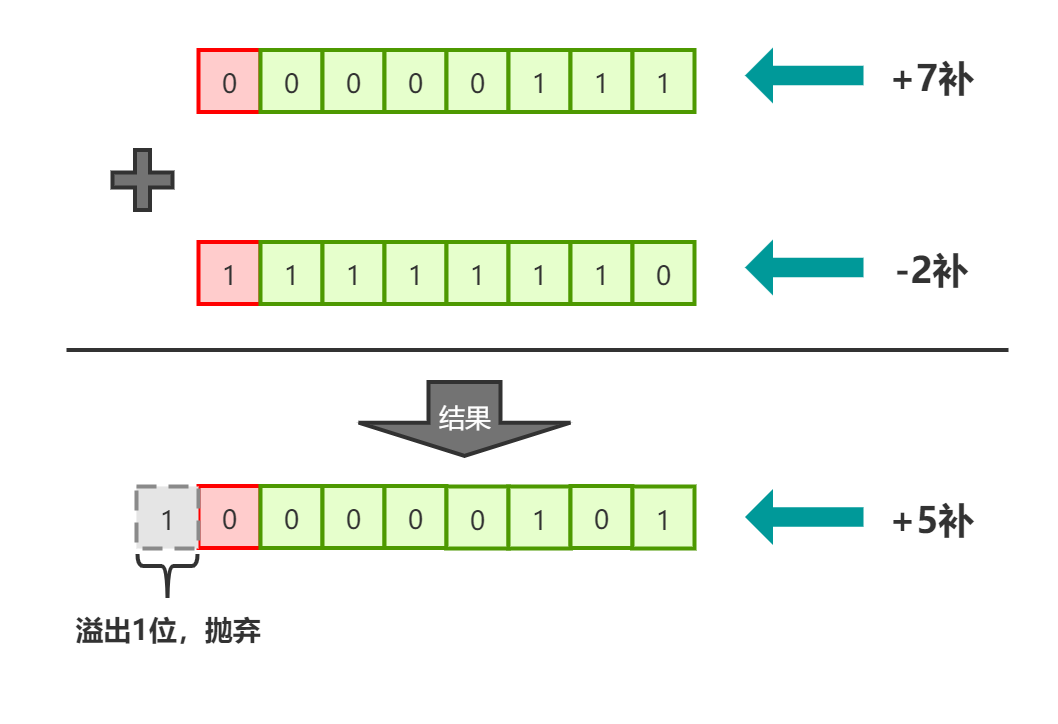
图4
ok,我们发现,用它们的补码做加法,得到的数值就是我们想要的正确答案,事实上,计算机并没有减法运算器,所有的减法运算,都是以一个正数加上一个负数的形式来交给加法运算器计算的,由于负数的符号位为1,虽然我们人是知道它的含义,但是作为计算机,它是不知道第一位是符号位的,它要做的就仅仅是让两个数相加而已,正是因为如此,我们才不能简简单单保存负数,通过图4我们知道,两个数的补码相加,可以得到一个准确的数值。
再举个相加结果为负数的例子,让两个负数相加:

图5
如果结果为负数的话,也是适用的,只是它仍然是以补码的形式存放的,需要转成原码才符合我们人的理解方式。
现在回到上面留下的问题,为什么byte的取值范围是-128~127呢?
我们之前按照图1里的理解,理所应当的以为它应该是-127~127的范围,那是因为我们按照图1的理解方式,数值就是以符号位+数值位的方式理解的(也就是按照原码的方式理解的),但是你可以想一下,如果按照图1那种理解方式,是不是会存在两个0值呢?
即:10000000和00000000,+0和-0;
其次如果站在机器角度上来说,所有的负数都很大,至少要比所有正数大,因为负数的最高位也就是符号位都是1,显然这是不对的,通过本节我们知道了,所有的数均通过自己的补码完成计算,如果将最后得到的结果转成原码,就是我们人眼可以理解的最终值(符号位+数值位),如果现在利用补码的方式做理解,符号位为0的数没啥好说的,自然取值区间为:0~127,但是符号位为1的负数呢?负数就存在一个特殊值(也就是我们之前片面理解的-0):10000000,如果按照原码理解它是-0,但我们前面说过,计算机里所有数字,都是以补码的方式参与运算的,而负数的补码不等于其原码,这个10000000在计算机里显然是某个负数的补码,那么问题就变的简单多了,即10000000是谁的补码呢?答案是:-128,这也是为什么负数的取值范围会比正数多一个的原因,byte类型如此,其它类型也是如此,比如int型的负数取值也比正数多1。
这一块的定义要清晰,对理解后面的位运算会有很大的帮助。
二、java中的位运算
2.1:与运算
与运算符号:&
与运算特点:1&1=1、1&0=0、0&1=0、0&0=0
现在我们来举一个例子:

图6
让我们再来试试负数:
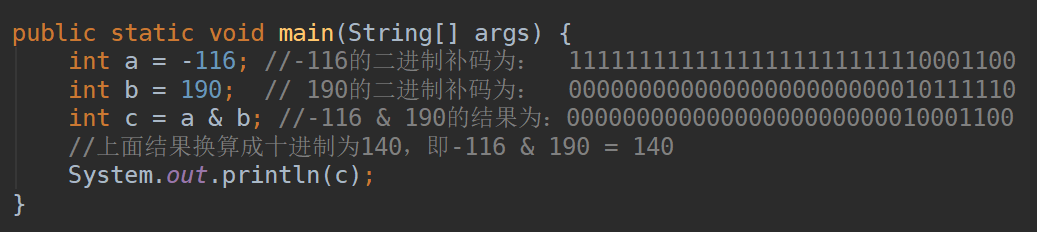
图7
2.2:或、异或
跟与运算的运算方式一致,只不过规则不太一样:
或运算符号:|
或运算规则:1|1=1、1|0=1、0|1=1、0|0=0
异或运算符号:^
异或运算规则:1^1=0、1^0=1、0^1=1、0^0=0
2.3:按位取反
取反符号:~
即一个数对自己取反,例如:
某个数字a的二进制为: 1010110
则~a为: 0101001
2.4:左移运算
左移运算符:<<
例如:
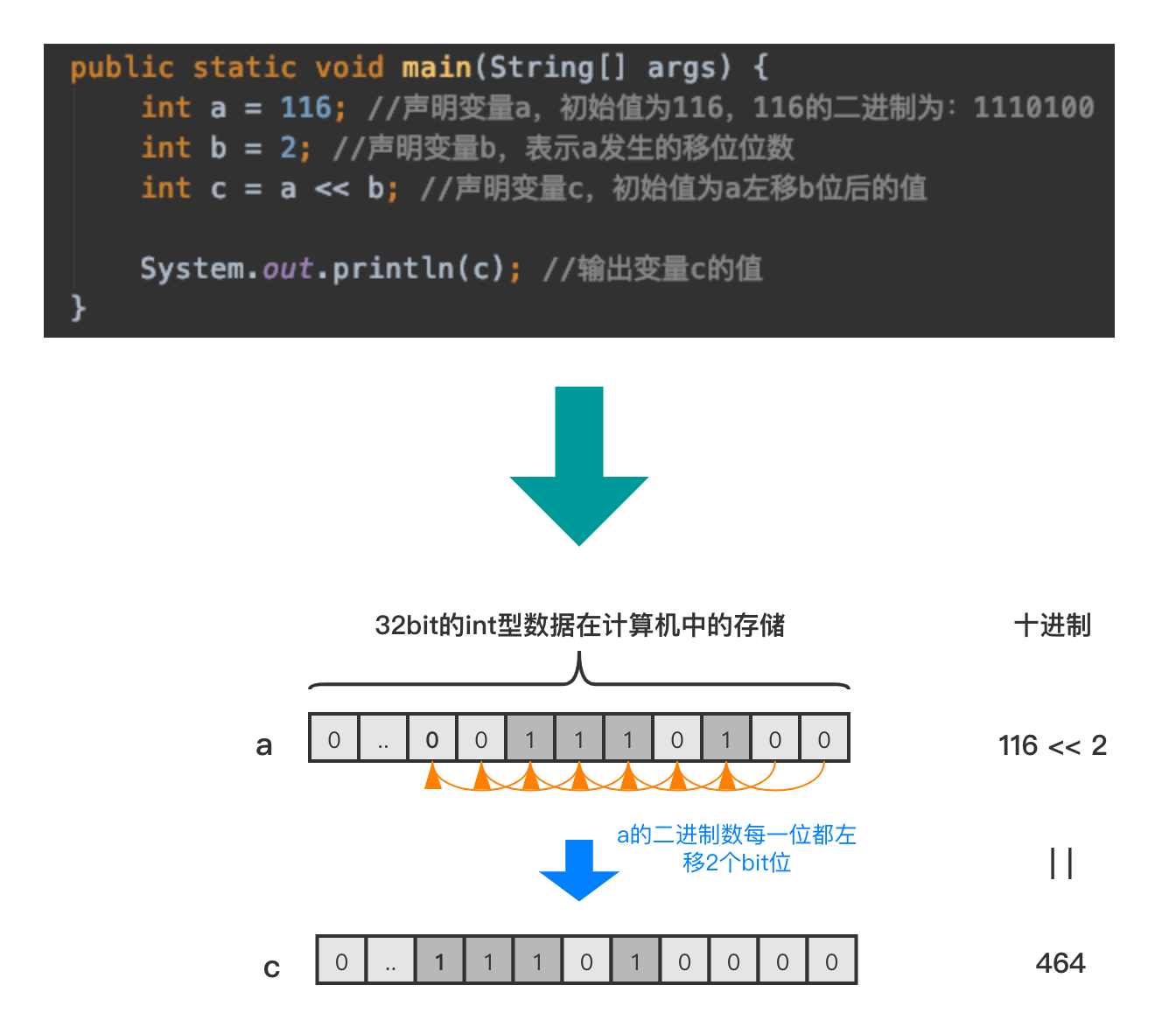
图8
位运算越界&数位抛弃:
图8中的116的二进制数的数值位为7位,符号位为0,此时如果左移超过24位,就会出现负数,为什么会这样?因为java中的位移越界时,java会抛弃高位越界部分,我们知道java里int类型的第一位是符号位,如果符号位是1,则表示其为负数,现在将数值位占7bit符号位为0的116左移24位,就会出现下方结果:
01110100000000000000000000000000
正好31位占全,顶至符号位,低位补0,我们称24为116的不越界的最大左移值,若超出这个值,就会越界,比如左移25位:
11101000000000000000000000000000
显然左移25位后会把数值位的1移动到符号位,这时它表示为一个负数的补码。根据这个规则,我们如果让其左移28位,则值为:
01000000000000000000000000000000
也就是十进制的1073741824,即:116 << 28 = 1073741824,那如果越界过多呢?比如int型的数据,左移32位:116 << 32 = 116
会发现,如果左移自己位数一样多的位数,那么这个数就等于它本身,因此运算符合以下规则:
设x为被位移值,y为本次位移的位数,z为x所属类型的最大存储位数:
x << y = x << (y%z)
如果是int型(32位,long型就用64代入计算),符合如下规则:
116 << 4 = 116 << (4%32) = 116 << 4 = 1856
116 << 32 = 116 << (32%32) = 116 << 0 = 116
116 << 36 = 116 << (36%32) = 116 << 4 = 1856
2.5:有符号右移运算&无符号右移运算
有符号右移运算符:>>
无符号右移运算符:>>>
例如:a >> b表示a右移b位,跟上面的左移例子一样,右移也会有越界问题,只是右移越界是从右边开始抛弃越界部分的,右移操作有符号位干扰,如果是正数右移,无此干扰项,因为符号位本就是0右移不会影响值的准确性,但如果是负数,第一位是符号位,且值为1,右移就有影响了,现在仍然以116为例:
正数右移:
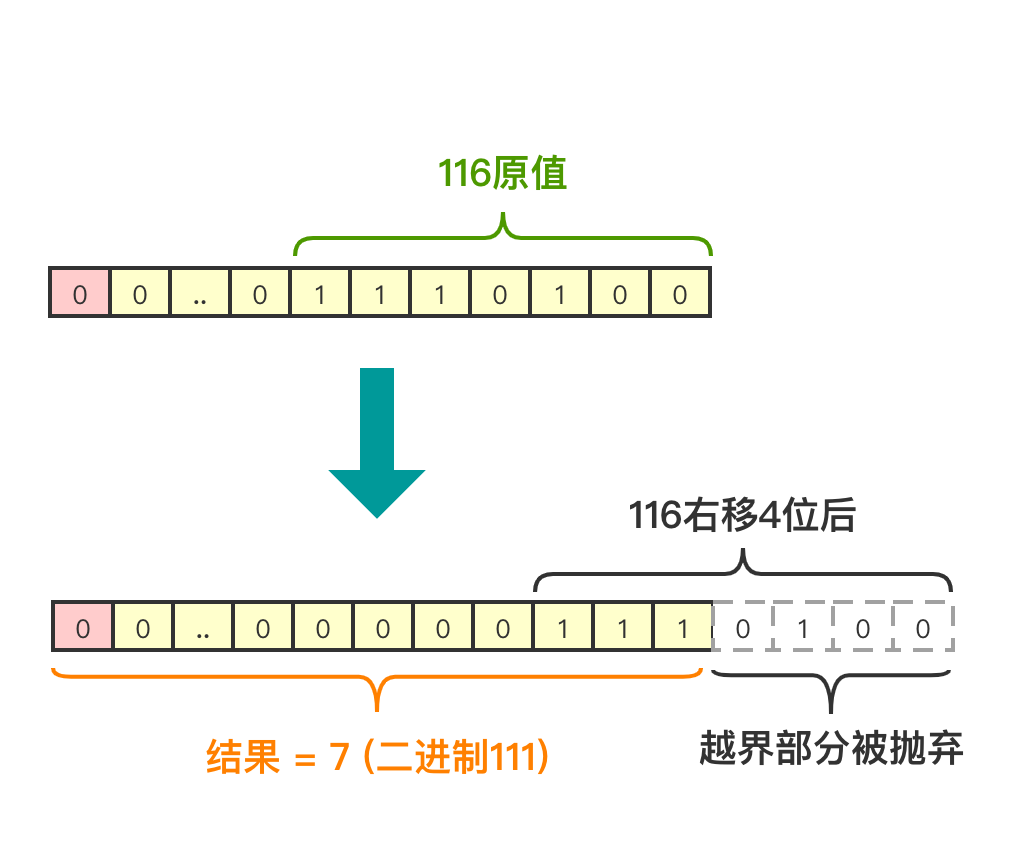
图9
上述是正数,右移无影响,但是负数,这里以-116为例,我们知道负数在计算机里是以补码的形式存储的,所以图里直接用-116的补码做运算,位移过程如下:
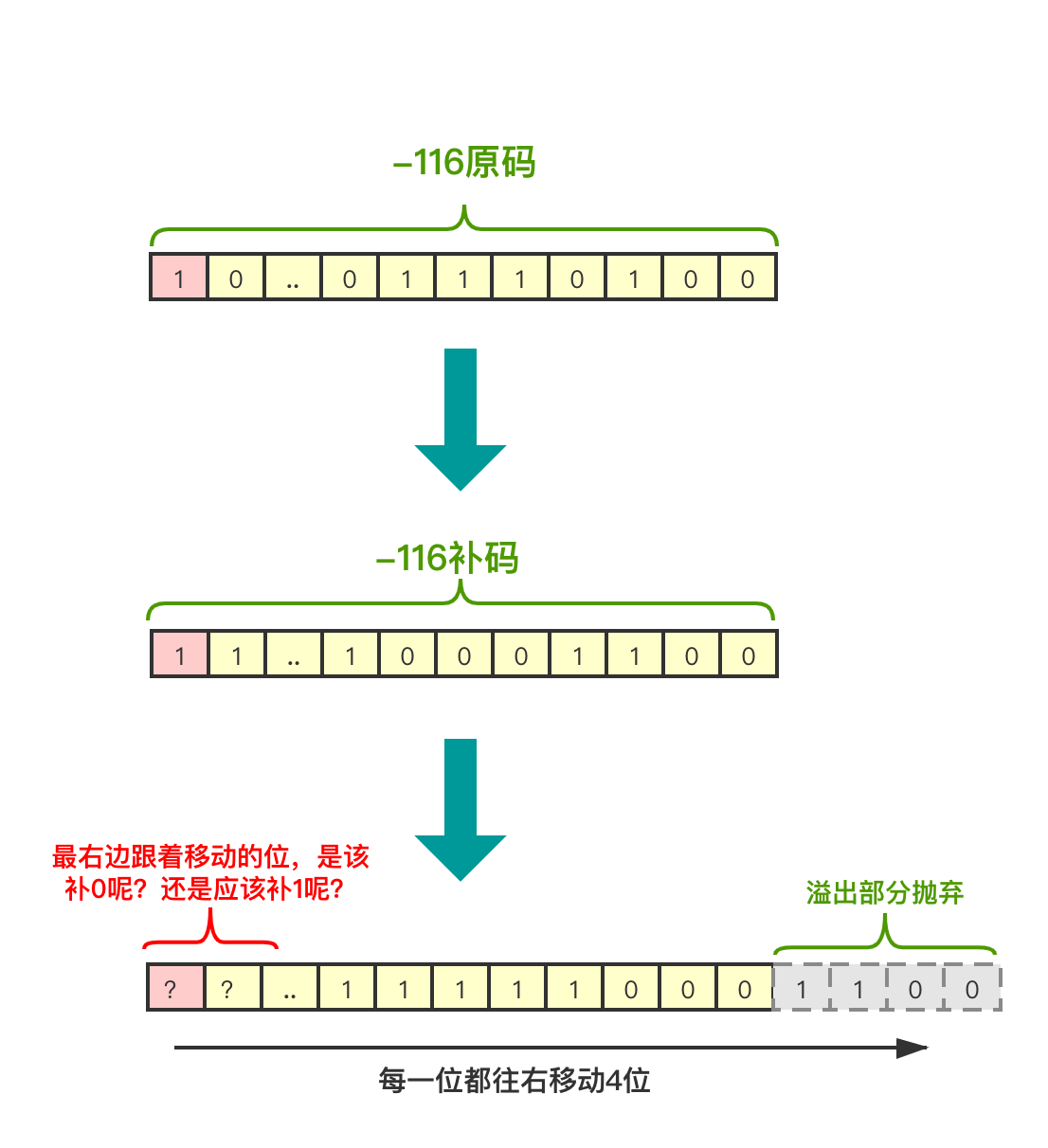
图10
你会发现右移跟左移不一样,左移是不用担心自己符号位存在“补位”问题的,但是右移存在,如图中-116右移4位后,左边第一位,也就是符号位,就面临着补位的问题,那我现在是该补1呢,还是补0呢?这也就是为什么右移操作会存在有符号右移和无符号右移两种移动方式:
☘️ 有符号右移:依照原符号位,如果原符号位是1,那么图4里需要补位的空位全部补1,如果原符号位为0,则全部补0
☘️ 无符号右移:无视原符号位,全部补0
现在让我们用有符号的方式将-116右移4位,即-116 >> 4,按照有符号的规则,补位符合原符号位,则右边4位全部补1:

图11
得到的仍然是个负数,它仍然是一个补码,图里展示不开,它的结果为:11111111111111111111111111111000,经转换可知它是-8的补码,即:-116 >> 4 = -8
现在再试试用无符号右移,根据无符号的特点,右移后的前四位无脑补0:
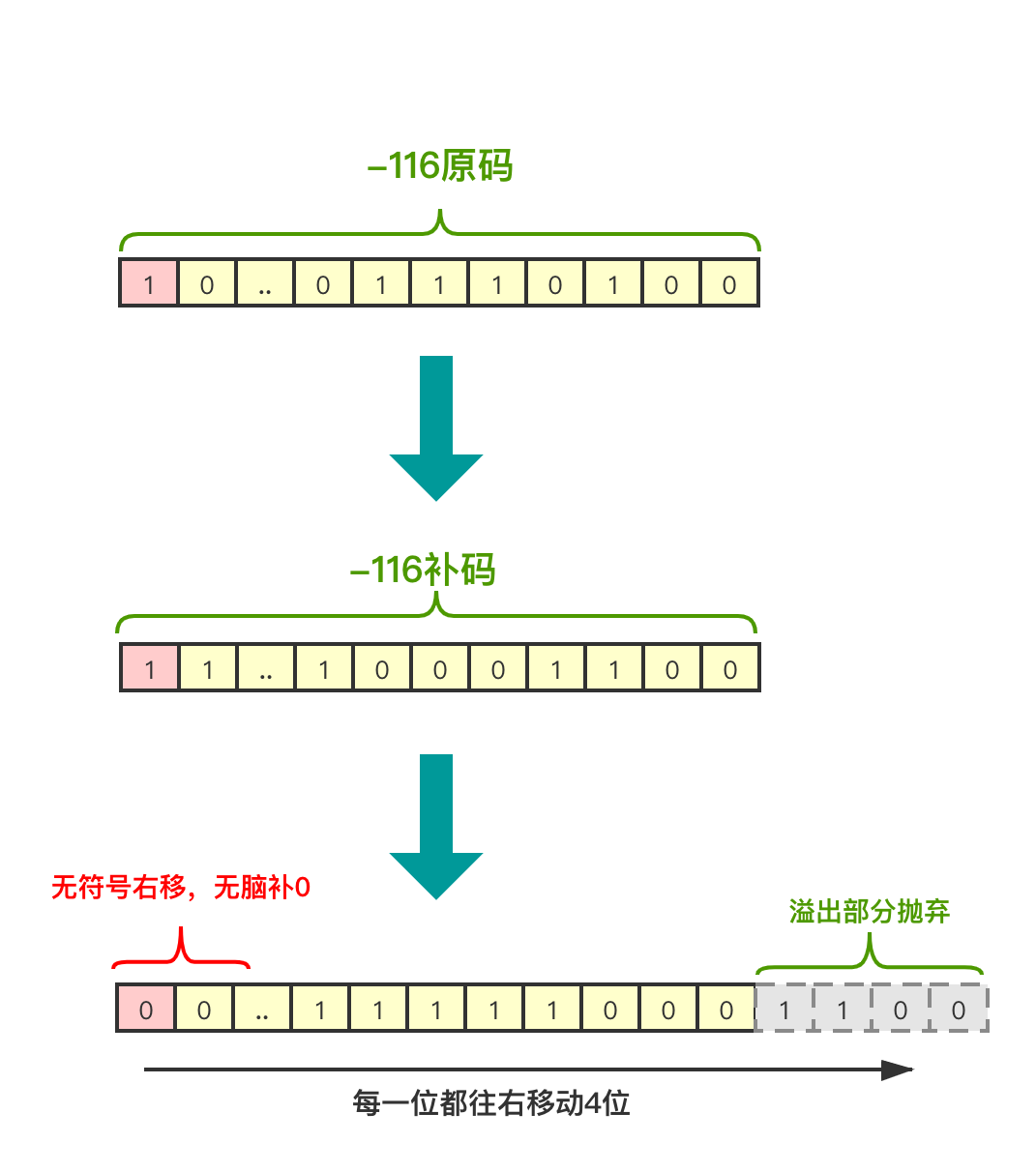
图12
图里展示不开,它的结果为:00001111111111111111111111111000
可见它是个正数,转换成十进制为:268435448,即:-116 >>> 4 = 268435448
最后说一下,跟左移一样,右移里不管是有符号还是无符号,也符合取余的方式,计算出位移的最终位数:
-116 >> 4 = -116 >> (4%32) = -116 >> 4 = -8
-116 >> 32 = -116 >> (32%32) = -116 >> 0 = -116
-116 >> 36 = -116 >> (36%32) = -116 >> 4 = -8
2.6:类型转换溢出
了解完位运算,来看一个比较实际的问题,看下面的代码:
long a = 8934567890233345621L;
int b = (int) a; //b的值为-1493678507
最终b的值是一个负数,这是由于long型64位,让int型强行接收,会出现位溢出的问题,这个流程如下:

图13
三、位运算在实际项目中的运用
位运算的性能是非常好的,相比运算流程,计算机更喜欢这种纯粹的逻辑门和移动位置的运算,但位运算在平常的业务代码里并不太常见,因为它的可读性不太好,但是我们仍然可以利用位运算来解决一些实际项目里的问题。
比如用来表示开关的功能,比如需求里经常有这种字段:是否允许xx(0不允许,1允许),是否有yy权限(0没有,1有),是否存在zz(0不存在,1存在)
上面只是举例,类似这种只有两种取值状态的属性,如果当成数据库字段放进去的话,太过浪费,如果之后又有类似的字段,又得新增数据库字段,为了只有两种取值的字段,实在是不太值得。
这个时候何不用一个字段来表示这些字段呢?你可能已经猜到要怎么做了:

图14
顶一个int型或者long型的字段,让它的每一个二进制位拥有特殊含义即可,然后按照位运算将其对应的位置上的数值变成0或1,那如何将某个数的二进制位第x位上的数值变成1或0呢?其实这在位图结构里经常用到,就是利用1这个特殊的值作位移运算后再与原值进行位运算,让我们看下这个过程:
把一个数的第2位的字符变成1,现在假设这个数初始化为0,int型,我们把它当成二进制展示出来:

图15
现在如何把这个数的第二位变成1呢?目前是这样做的:
0 | 1 << 1
即原值跟1左移1位后的值作或运算,先来看看1 << 1的结果:

图16
然后拿着图16的结果,跟原数(也就是0)进行或运算:
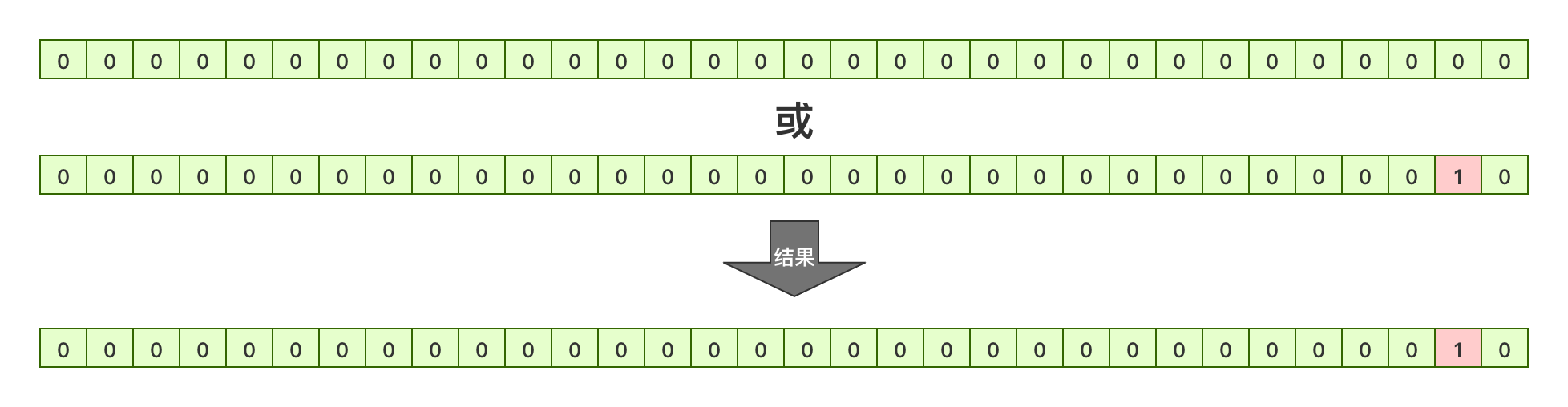
图17
可以看到,原数的第二位已经被置为1了,它的十进制对应2,其它位的数置为1也大同小异,例如,现在让第6位也变成1只需要:
2 | 1 << 5
即拿着原值(现在为2)跟1左移5位后的数做或运算,这个流程如下:
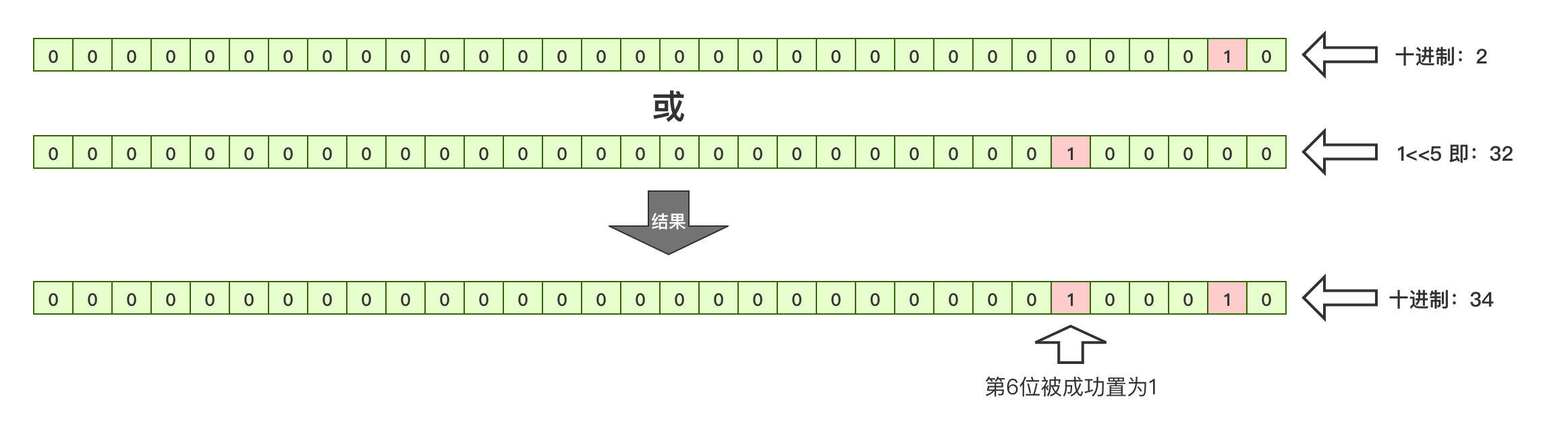
图18
看完了把某个位置的数值置为1,那如何把某位设置为0呢?我们现在把图18里的结果的第6位重新置回0,目前的做法为:
34 & ~(1 << 5)
即拿着原值(经过上面几步的运算,现在值为34)跟1左移5位按位取反后的数做与运算,来看下这个流程:

图19
经过上面的流程,就可以把原值的第6位变成0了。
那么我们知道了让一个数的二进制位的某位变成0或1的方法,那如何知道一个数的某位上究竟是0还是1呢?毕竟我们业务代码需要知道第几位代表什么意思并且获取到对应位置上的值。
假如我现在想知道十进制int型数34的第6位是0还是1,写法如下:
34 >> 5 & 1
即让原值(34)右移5位后跟1做与运算,来看下这个流程:

图20
由图可以看出,想要知道一个数的第几位是1还是0,只需要将其对应位置上的值“逼”到最后一位,然后跟1相与即可,如果对应位置上的值是0,那么与1相与后的结果一定为0,反之一定为1.
☘️ 总结
到这里已经说完了为什么要用一个数表示那么多开关,以及如何给一个开关位设置对应的开关值,以及如何找到对应开关位的值,有了这些操作,我们再也不需要为这种只有0和1取值的字段新增数据库字段了,因为一个int型的数字,就可以表达32个开关属性,如果超了,还可以扩成64位的long型~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号