bzoj 1179[Apio2009]Atm (tarjan+spfa)

题目

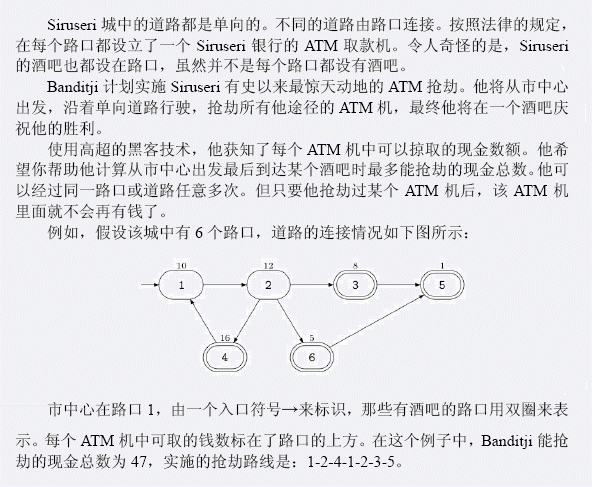
输入

第一行包含两个整数N、M。N表示路口的个数，M表示道路条数。接下来M行，每行两个整数，这两个整数都在1到N之间，第i+1行的两个整数表示第i条道路的起点和终点的路口编号。接下来N行，每行一个整数，按顺序表示每个路口处的ATM机中的钱数。接下来一行包含两个整数S、P，S表示市中心的编号，也就是出发的路口。P表示酒吧数目。接下来的一行中有P个整数，表示P个有酒吧的路口的编号

输出

输出一个整数，表示Banditji从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。

样例输入

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1
5
1 4
4
3
5
6
样例输出

47
提示

50%的输入保证N, M<=3000。所有的输入保证N, M<=500000。每个ATM机中可取的钱数为一个非负整数且不超过4000。输入数据保证你可以从市中心沿着Siruseri的单向的道路到达其中的至少一个酒吧。

 这道题我们需要用tarjan+spfa（用来跑最长路）

 首先要做的是把图上的点跑一边tarjan求出所有的强连通分量，把强连通分量上的点的父节点都设成该强连通分量的根

              //因为强连通分量上的点只要能到达一个就可以到达该强连通分量上的其它点，并且一条路可以走很多遍。

 再把所有强连通分量中的除了根以外的点上的值全部加到根上。

 然后将所有不在强连通分量中的点以及所有强连通分量的根为新的点，重新建图

 对新建的图进行spfa求最长路

 最后找出所有酒吧的父节点找出来，找出这些节点中到起点值最大的

              //因为强连通分量上的点只要能到达一个就可以到达该强连通分量上的其它点，并且一条路可以走很多遍。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int cnt, hh[510000], hhh[510000], stack[510000];
int dfn[510000], low[510000], num, ans, q, top, w[510000];
int father[510000], dd[510000], j, n, h, t, l[510000], z, x, y, m, s, p;
bool d[510000];
struct node
{
    int v, next;
};
node b[510000], ss[510000];
void add(int aa, int bb)//连边
{
    b[++cnt].v = bb;
    b[cnt].next = hh[aa];
    hh[aa] = cnt;
}
void addd(int aa, int bb)//连接新建图上的边
{
    ss[++cnt].v = bb;
    ss[cnt].next = hhh[aa];
    hhh[aa] = cnt;
}



void tarjan(int k)
{
    int i;
    dfn[k] = low[k] = ++num;
    stack[++top] = k;
    d[k] = true;
    for(i = hh[k]; i != 0; i = b[i].next)
    {
        int e = b[i].v;
        if(!dfn[e])
        {
            tarjan(e);
            low[k] = min(low[k], low[e]);
        }
        else if(d[e] == true)
        {
            low[k] = min(low[k], dfn[e]);
        }
    }
    if(dfn[k] == low[k])
    {
        d[k] = false;
        father[k] = k;
        while(stack[top] != k)
        {
            w[k] += w[stack[top]];
            father[stack[top]] = k;
            d[stack[top--]] = false;
        }
        top--;
    }

}
void rebuild()
{
    cnt = 0;
    int i;
    for(i = 1; i <= n; i++)
    {
        for(j = hh[i]; j != 0; j = b[j].next)
        {
            t = b[j].v;
            if(father[i] == father[t])continue;
            addd(father[i], father[t]);
        }
    }
}
void spfa()
{
    int i;
    q = s;
    memset(d, 0, sizeof(d));
    h = 0, t = 0;
    l[q] = w[q];
    d[q] = true;
    while(1)
    {
        if(h > t)break;

        for(i = hhh[q]; i != 0; i = ss[i].next)
        {
            z = ss[i].v;
            if(l[q] + w[z] > l[z])
            {
                l[z] = l[q] + w[z];
                if(d[z])continue;
                dd[++t] = z;
                d[z] = true;
            }
        }
        d[q] = false;
        q = dd[++h];
    }
}
int main()
{
    int i;
    scanf("%d %d", &n, &m);
    for(i = 1; i <= m; i++)
    {
        scanf("%d %d", &x, &y);
        add(x, y);
    }
    for(i = 1; i <= n; i++)
    {
        scanf("%d", &w[i]);
    }
    scanf("%d %d", &s, &p);
    for(j = 1; j <= n; j++)
    {
        if(!dfn[j])tarjan(j);
    }
    rebuild();//利用tarjan求出所有强连通分量

    s = father[s];//如果起点在一个强连通分量中，那么将起点换成该强连通分量的根
                  //因为强连通分量上的点只要能到达一个就可以到达该强连通分量上的其它点，并且一条路可以走很多遍。
                  //重要的事说三遍

    spfa();//利用spfa求出最长路

    for(i = 1; i <= p; i++)
    {
        scanf("%d", &q);
        ans = max(ans, l[father[q]]);
    }
    printf("%d", ans);
    return 0;
}