图论

/**
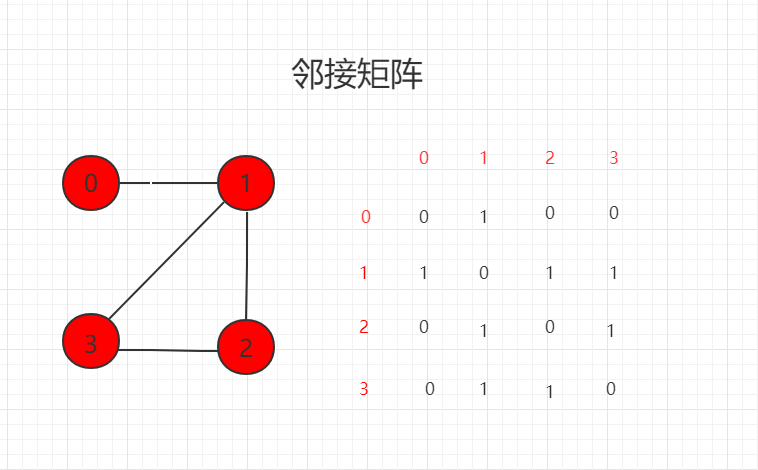
 * 邻接矩阵
 */
export class DenseGraph {
  // 节点数
  n: number
  // 边数
  m: number
  // 是否为有向图
  directed: boolean
  // 图得具体数据
  g: boolean[][]
  constructor(n: number, directed: boolean) {
    console.assert(n >= 0, 'n必须大于0')
    this.n = n
    this.m = 0
    this.directed = directed
    // g初始化为n*n得布尔矩阵,每个g[i][j]均为false,表示没有任何边
    this.g = this.twoArr(n)
  }
  // 返回节点个数
  V() {
    return this.n
  }
  // 返回边得个数
  E() {
    return this.m
  }
  //向图中添加一个边
  add(v: number, w: number): void {
    try {
      console.assert(v >= 0 && v < this.n, 'v必须大于等于0,小于n')
      console.assert(w >= 0 && w < this.n, 'w必须大于等于0,小于n')
      if (this.hasEdge(v, w)) {
        return
      }
      this.g[v][w] = true
      //如果为无向图就职位true
      if (!this.directed) {
        this.g[w][v] = true
      }
      this.m++
    } catch (error) {}
  }
  //验证图中是否有从v到w得边
  hasEdge(v: number, w: number): boolean {
    try {
      console.assert(v >= 0 && v < this.n, 'v必须大于等于0,小于n')
      console.assert(w >= 0 && w < this.n, 'w必须大于等于0,小于n')
      return this.g[v][w]
    } catch (error) {}
    return false
  }
  //构造一个二位数组
  twoArr(n: number) {
    let aa = []
    for (let i = 0; i < n; i++) {
      aa[i] = new Array()
      for (let j = 0; j < n; j++) {
        aa[i][j] = false
      }
    }
    return aa as boolean[][]
  }
}
let graph1 = new DenseGraph(4, true)
graph1.add(3, 3)
console.log(graph1.g)

/**
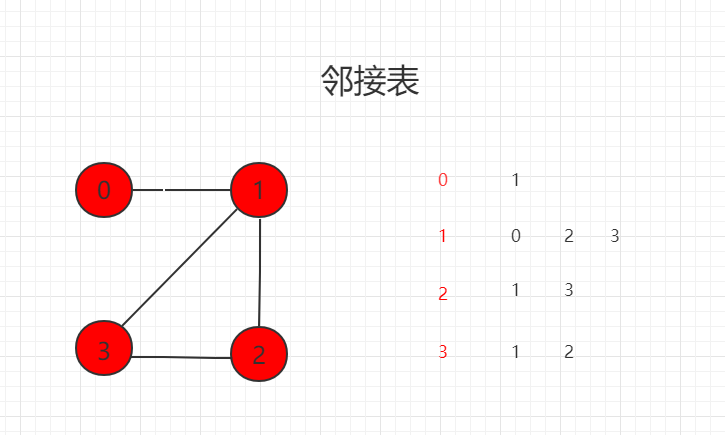
 * 邻接表
 */
export class SparseGraph {
  // 节点数
  n: number
  // 边数
  m: number
  // 是否为有向图
  directed: boolean
  // 图得具体数据
  g: number[][]
  constructor(n: number, directed: boolean) {
    console.assert(n >= 0, 'n必须大于0')
    this.n = n
    this.m = 0
    this.directed = directed
    // g初始化为n*n得布尔矩阵,每个g[i][j]均为false,表示没有任何边
    this.g = this.twoArr(n)
  }
  // 返回节点个数
  V() {
    return this.n
  }
  // 返回边得个数
  E() {
    return this.m
  }
  //向图中添加一个边
  add(v: number, w: number): void {
    try {
      console.assert(v >= 0 && v < this.n, 'v必须大于等于0,小于n')
      console.assert(w >= 0 && w < this.n, 'w必须大于等于0,小于n')
      this.g[v].push(w)
      if (v != w && !this.directed) {
        this.g[w].push(v)
      }
      this.m++
    } catch (error) {}
  }
  //验证图中是否有从v到w得边
  hasEdge(v: number, w: number): boolean {
    try {
      console.assert(v >= 0 && v < this.n, 'v必须大于等于0,小于n')
      console.assert(w >= 0 && w < this.n, 'w必须大于等于0,小于n')
      for (let i = 0; i < this.g[v].length; i++) {
        if (this.g[v][i] === w) {
          return true
        }
        return false
      }
    } catch (error) {}
    return false
  }
  //构造一个二位数组
  twoArr(n: number) {
    let aa = []
    for (let i = 0; i < n; i++) {
      aa[i] = new Array()
    }
    return aa as number[][]
  }
}

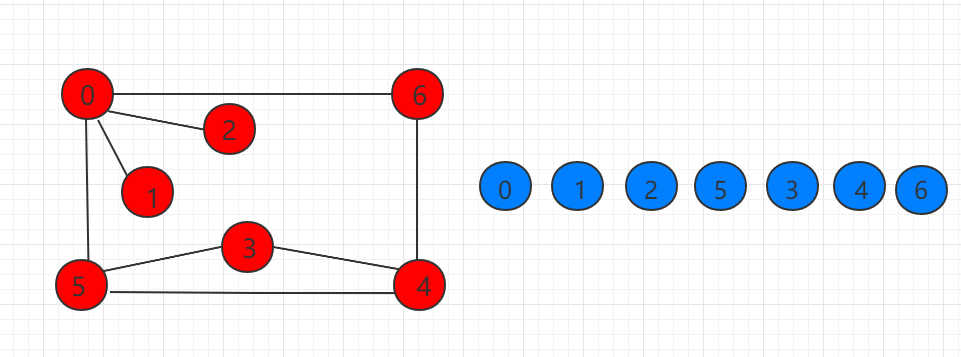
深度优先搜索求出图的联调分量

//求出无权图的联调分量
  const components = () => {
    let graph2 = new DenseGraph(7, false)
    graph2.add(0, 1)
    graph2.add(0, 2)
    graph2.add(0, 5)
    graph2.add(0, 6)
    graph2.add(3, 4)
    graph2.add(3, 5)
    graph2.add(4, 5)
    graph2.add(4, 6)
    console.log(graph2.g)
    console.log(graph2.V())
    // 记录节点是否被访问
    let visited: Boolean[] = new Array(graph2.V()).fill(false)
    // 代表每个节点所对应的联调分量标记
    let id: number[] = new Array(graph2.V()).fill(-1)
    // 记录联调分量个数
    let count = 0
    // 记录深度优先搜索过程
    let dfsArr: number[] = []
    //图得深度优先搜索
    const dfs = (v: number) => {
      dfsArr.push(v)
      visited[v] = true
      id[v] = count
      for (let i of graph2.adj(v)) {
        if (!visited[i]) {
          dfs(i)
        }
      }
    }
    for (let i = 0; i < graph2.V(); i++) {
      if (!visited[i]) {
        console.log(`${i}0.0`, visited[i])
        dfs(i)
        count++
      }
    }
    console.log('count', count)
    console.log(dfsArr)
    console.log(graph2.adj(0))
    // console.log('id', id)
    // console.log('visited', visited)
  }

 //寻路算法,寻找图graph2从s点到其他点的路径
  const shortestPath = (s: number, w: number) => {
    let graph2 = new DenseGraph(7, false)
    graph2.add(0, 1)
    graph2.add(0, 2)
    graph2.add(0, 5)
    graph2.add(0, 6)
    graph2.add(3, 4)
    graph2.add(3, 5)
    graph2.add(4, 5)
    graph2.add(4, 6)
    // 记录节点是否被访问
    let visited: Boolean[] = new Array(graph2.V()).fill(false)
    // from[i]表示查找的路径上i的上一个节点
    let from: number[] = new Array(graph2.V()).fill(-1)
    // ord[i]表示i节点在路径中的次序
    let ord: number[] = new Array(graph2.V()).fill(-1)
    let q: number[] = []
    let bfs: number[] = []
    q.push(s)

    visited[s] = true
    ord[s] = 0
    while (q.length > 0) {
      let v = q.shift()
      bfs.push(v)
      for (let i of graph2.adj(v)) {
        if (!visited[i]) {
          q.push(i)
          visited[i] = true
          from[i] = v
          ord[i] = ord[v] + 1
        }
      }
    }
    // 查询s点到w点是否有路径
    const hasPath = (w: number) => {
      return visited[w]
    }
    //查看s点到w点的最短路径长度
    const length = (w: number) => {
      return ord[w]
    }
    //查询s点到w点的路径,存放在vec中
    const path = (w: number) => {
      let s = []
      let p = w
      while (p !== -1) {
        s.push(p)
        p = from[p]
      }
      let res = []
      while (s.length > 0) {
        res.push(s.pop())
      }
      return res
    }
    //打印出s点到w点的路径
    const showPath = (w: number) => {
      let vec = path(w)
      for (let i = 0; i < vec.length; i++) {
        console.log(vec[i])
        if (i === vec.length - 1) {
          console.log('结束了')
        } else {
          console.log('->')
        }
      }
    }
    console.log('bfs', bfs)
    console.log('form', from)
    console.log('ord', ord)
    console.log('haspath', hasPath(w))
    console.log('haspath', length(w))
    showPath(w)
  }