用 STL 红黑树求第 K 大
众所周知, STL 中的 \({\tt std:\,:set}\) 和 \({\tt std:\,:map}\) 内部使用红黑树来维护数据,于是有着极为优秀的时间效率:在 \(O(\log n)\) 级别的时间复杂度内进行插入、删除或查询。
同时,诸如红黑树一类的平衡树在 OI 中也有着广泛的应用。那么能否直接使用 STL 中现成的 \({\tt set}\) 或 \({\tt map}\) 来代替我们自己写的平衡树呢?
显然是不行的,否则广大 OIer 就不会深陷写平衡树的疾苦了。
于是本文将尝试解决该问题。
写在前面
- 本文的方法并不是 OI 或其他任何地方中最好的方法。如果你想在 OI 中使用现成的平衡树,那么 \({\tt \_\_gnu\_pbds:\,:tree}\) 才是你的第一选择。
- 虽然本文旨在用 STL 代替自己写平衡树,但读者仍需已掌握平衡树(不一定是红黑树)的原理和基础写法。
- 读者需对 C++ 语法较熟练地掌握。
- 读者需可以接受 STL 码风。
- 请读者接受我的码风。
思路
首先,我们不能直接使用 STL 的原因是, STL 没有维护每个子树大小,导致我们不能在 \(O(\log n)\) 的时间内完成求第 k 大和求排名操作。
为解决这个问题,我们尝试自己帮助 STL 来维护子树大小。
\({\tt set}\) 、 \({\tt multiset}\) 、 \({\tt map}\) 和 \({\tt multimap}\) 内部使用的红黑树相同:定义在头文件 stl_tree.h 中的 \({\tt std:\,:\_Rb\_tree}\) 。
原则上, \({\tt \_Rb\_tree}\) 是 STL 的内部容器,不对外开放。但实际上, STL 并没有从语法规则上限制我们,所以我们仍然可以直接使用。
我选择了通过继承 \({\tt \_Rb\_tree}\) 来实现我们的平衡树。
STL 红黑树的结构
\({\tt \_Rb\_tree}\) 的数据结构由以下 3 部分构成:
- 节点(Node): \({\tt \_Rb\_tree\_node}\)
- 数据头(Header cell): \({\tt \_Rb\_tree\_header}\)
- 迭代器(Iterator): \({\tt \_Rb\_tree\_iterator}\)
P.s. 1 分配器(Allocator)等不是本文重点,所以不作讨论。
P.s. 2 以上中文翻译都是我自己瞎编的。为了严谨,后文将尽量使用原文。
Node
\({\tt \_Rb\_tree\_node}\) 继承自基类 \({\tt \_Rb\_tree\_node\_base}\)
STL 将不使用模板的数据放在基类中,将使用模板的数据放在子类中。
// 以下省略了部分内容
// 基类
struct _Rb_tree_node_base
{
// 以下定义节点基类的指针。
// 注意。这是一个很重要的数据类型。
typedef _Rb_tree_node_base* _Base_ptr;
typedef const _Rb_tree_node_base* _Const_Base_ptr;
_Rb_tree_color _M_color; // 节点颜色。此数据于本文暂无用处。
_Base_ptr _M_parent; // 指向父节点
_Base_ptr _M_left; // 指向左儿子节点
_Base_ptr _M_right; // 指向右儿子节点
};
// 子类
template<typename _Val>
struct _Rb_tree_node : public _Rb_tree_node_base
{
typedef _Rb_tree_node<_Val>* _Link_type;
_Val _M_value_field;
// 这里其实是一种不准确的表示。
// C++11 之后,改为了
// __gnu_cxx::__aligned_membuf<_Val> _M_storage;
// 但可以简单理解为将节点的值定义在此。
};
值得注意的是,子类 \({\tt \_Rb\_tree\_node}\) 并不经常使用。相反,更多的时候我们以指针 \({\tt \_Base\_ptr}\) 的形式使用其基类 \({\tt \_Rb\_tree\_node\_base}\) 。
Header Cell
我们自己写平衡树时,常常在树中加入哨兵节点来防止越界。 STL 通过 \({\tt \_Rb\_tree\_header}\) 来实现该功能。
除此以外, \({\tt \_Rb\_tree\_header}\) 还帮助实现 \(O(1)\) 的 begin() 方法,和 \(O(n)\) 的通用合并等算法;帮助初始化红黑树,和记录树的大小。
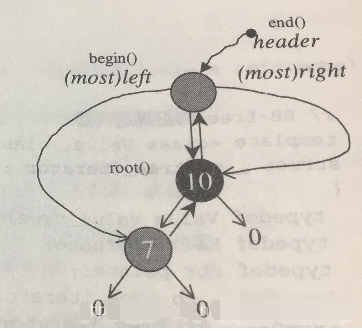
\({\tt \_Rb\_tree\_header}\) 内部有一个 \({\tt \_Rb\_tree\_node\_base}\) 类型的节点,名为 _M_header 。
_M_header 与红黑树的根节点互为父节点,若红黑树为空,则 header 的父节点指向空指针。
_M_header 的左儿子指向红黑树中的最小值,右儿子指向最大值。
struct _Rb_tree_header
{
_Rb_tree_node_base _M_header;
size_t _M_node_count; // Keeps track of size of tree.
// ...
};
在 \({\tt \_Rb\_tree}\) 中, \({\tt \_Rb\_tree\_header}\) 并不被直接使用,而是被继承到 \({\tt \_Rb\_tree}\) 内部的一个名为 \({\tt \_Rb\_tree\_impl}\) 的类型中。
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc = allocator<_Val> >
class _Rb_tree
{
// ...
protected:
template<typename _Key_compare>
struct _Rb_tree_impl
: public _Node_allocator
, public _Rb_tree_key_compare<_Key_compare>
, public _Rb_tree_header // 此处继承
{
// ...
};
_Rb_tree_impl<_Compare> _M_impl; // 此处定义对象
// ...
}
可见,之后我们对 header 的使用都需要通过 _M_impl._M_header 来获取。并且,我们应该注意维护 _M_impl._M_node_count 的值来确保 size() 方法的正确性。
Iterator
迭代器在本文的一个重要用处是,通过 \({\tt \_Base\_ptr}\) 获取对应节点上的值。
template<typename _Tp>
struct _Rb_tree_iterator
{
typedef _Rb_tree_node_base::_Base_ptr _Base_ptr; // 这个类型真的很重要
typedef _Rb_tree_node<_Tp>* _Link_type; // 节点子类的指针
_Base_ptr _M_node; // 迭代器指向的实际节点
_Tp* operator->() const // 取值
{ return static_cast<_Link_type>(_M_node)->_M_valptr(); }
// ...
};
之后我们会使用 _M_node 获取迭代器指向的节点,使用 operator->() 来取值。
stl_tree.h 的文件结构
放在这里作为补充。
部分内容有所省略。
namespace std
{
enum _Rb_tree_color { _S_red = false, _S_black = true };
struct _Rb_tree_node_base;
template<typename _Key_compare>
struct _Rb_tree_key_compare;
struct _Rb_tree_header;
template<typename _Val>
struct _Rb_tree_node;
template<typename _Tp>
struct _Rb_tree_iterator;
template<typename _Tp>
struct _Rb_tree_const_iterator;
// 插入平衡函数的声明
void
_Rb_tree_insert_and_rebalance(const bool __insert_left,
_Rb_tree_node_base* __x,
_Rb_tree_node_base* __p,
_Rb_tree_node_base& __header) throw ();
// 删除平衡函数的声明
_Rb_tree_node_base*
_Rb_tree_rebalance_for_erase(_Rb_tree_node_base* const __z,
_Rb_tree_node_base& __header) throw ();
// 红黑树本体
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc = allocator<_Val> >
class _Rb_tree;
// 之后是部分成员函数的实现
// ...
}
完成自己的平衡树
\({\tt \_Rb\_tree}\) 的定义
\({\tt \_Rb\_tree}\) 的声明源码:
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc = allocator<_Val> >
class _Rb_tree;
其中五个模板参数依次是:键的类型,值的类型,通过值获取键的仿函数,仿函数比较器,内存分配器。
使用时我们可以直接套用 \({\tt set}\) 中的用法。
// 以下代码来自头文件 stl_set.h
template<typename _Key, typename _Compare = std::less<_Key>,
typename _Alloc = std::allocator<_Key> >
class set
{
// ...
private:
typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
key_compare, _Key_alloc_type> _Rep_type;
_Rep_type _M_t; // Red-black tree representing set.
// ...
}
我们一股脑地把键和值设成一样的就行了:
// 可以定义一个 int 型的红黑树
std::_Rb_tree<int, int, std::_Identity<int>, std::less<int> > st;
为了方便,接下来我将使用以下这段代码来简化之后的定义:
template<typename _Tp>
using rb_tree = std::_Rb_tree<_Tp, _Tp, std::_Identity<_Tp>, std::less<_Tp> >;
// 例:定义一个 int 型的红黑树
rb_tree<int> st;
节点定义
为了实现查询第 k 大和查询排名的功能,我们需要自己重新定义节点,来维护子树大小。
同时我们要维护一个副本数,来减少时间常数,并协助之后的删除。
P.s. 副本数指相同值的个数。如果往平衡树中插入了多个相同值,则记录为副本数量,而不是在此新建节点。
template<typename _Val>
struct my_tree_node
{
_Val value_field; // 值字段
int subtree_size; // 子树大小
int copies_count; // 副本数
my_tree_node() : value_field() { }
my_tree_node(const _Val& __val) : value_field(__val) { } // 这个构造函数必须有
// 需重载小于号
bool operator < (const my_tree_node& __x) const
{ return value_field < __x.value_field; }
};
注意:节点必须有一个传值的构造函数。
平衡树
我们的平衡树继承自 \({\tt \_Rb\_tree}\)
template<typename _Tp>
using rb_tree = std::_Rb_tree<_Tp, _Tp, std::_Identity<_Tp>, std::less<_Tp> >;
template<typename _Val>
struct my_tree_node;
template<typename _Tp>
struct my_tree : rb_tree<my_tree_node<_Tp> >
{
typedef rb_tree<my_tree_node<_Tp> > Base; // 红黑树基类
typedef typename Base::iterator iterator; // 迭代器
typedef typename Base::_Base_ptr _Base_ptr; // 极为重要的类型
my_tree_node<_Tp> null; // 定义一个空节点
_Base_ptr root(); // 根节点
void pushup(_Base_ptr); // 维护子树大小信息
void insert(const _Tp&); // 按值插入
void erase(const _Tp&); // 按值删除
const _Tp& kth(int); // 第 k 大(小)
int rank(const _Tp&); // 求排名
const _Tp& predecessor(const _Tp&); // 求前驱
const _Tp& successor(const _Tp&); // 求后继
};
一些约定和提醒
为了方便,在此我们有一些约定,和宏定义。
节点数据的表示方法
对于节点,定义以下表示方法:
fa(x):father,节点 x 的父节点。lc(x):left child,节点 x 的左儿子。rc(x):right child,节点 x 的右儿子。val(x):value,节点 x 的值。siz(x):size,节点 x 的子树大小。cnt(x):count,节点 x 的副本数。
注意:以上的“ x ”都应当是重要的 \({\tt \_Base\_ptr}\) 类型。
具体地,使用宏定义如下:
#define fa(x) ( (x)->_M_parent )
#define lc(x) ( (x) == 0 ? 0 : (x)->_M_left )
#define rc(x) ( (x) == 0 ? 0 : (x)->_M_right )
#define val(x) ( (x) == 0 ? null.value_field : iterator(x)->value_field )
#define siz(x) ( (x) == 0 ? null.subtree_size : iterator(x)->subtree_size )
#define cnt(x) ( (x) == 0 ? null.copies_count : iterator(x)->copies_count )
值得注意的细节:
- 参数需为 \({\tt \_Base\_ptr}\) 类型。
- 注意打括号,养成好习惯。
- 指针需要判空。如果是空指针则返回
null节点的值。(想一想,为什么不直接返回 0,而是使用一个空节点?) - 父指针可以不用判空。(想一想,为什么)
- 通过把 \({\tt \_Base\_ptr}\) 类型转换为 \({\tt iterator}\) 类型,来获取我们节点的数据。
- 一个更标准的写法,是将上面宏定义中所有的
0全部换为 C++ 关键字nullptr。
后文将使用上述表示方法。
其他注意事项
\({\tt \_Base\_ptr}\) 类型真的十分重要,下文将多次出现。如果你忘记了它的意义,请回顾上文“ Node ”章节。
由于语法限制,凡是使用来自基类 \({\tt \_Rb\_tree}\) 的类型、成员、方法等,都需要加上域解析 Base::。其中 Base 类型的定义见上文“ \({\tt \_Rb\_tree}\) 的定义”章节。
可以善用 auto 减少写程序的负担。
成员函数
root
root() 可以有几种写法。
一种较好的写法是利用上文说过的“ _M_impl._M_header 与红黑树的根节点互为父节点”。
_Base_ptr root() { return Base::_M_impl._M_header._M_parent; }
const _Base_ptr root() const { return Base::_M_impl._M_header._M_parent; }
另一种偷懒的写法是直接引用基类的函数。
_Base_ptr root() { return Base::_M_root(); }
当然你根本就可以不写 root() 函数,每次直接调用 Base::_M_root() 就可以了。
update:为什么不用宏定义……
#define root() ( Base::_M_root() )
pushup
非常地正常。
注意,我们都是对 \({\tt \_Base\_ptr}\) 这个类型进行操作。
void pushup(_Base_ptr x) {
if (x == 0) return;
siz(x) = siz(lc(x)) + siz(rc(x)) + cnt(x);
}
insert
\({\tt \_Rb\_tree}\) 提供了两种插入方式。
// 方式一:
// 如果插入的值已经存在,则不插了。
// 返回值:已有值的迭代器,是否插入成功
pair<iterator, bool>
_M_insert_unique(const value_type& __x);
// 方式二:
// 不论插入的值是否已经存在,都新建一个节点把它插进去
// 返回值:新节点的迭代器
iterator
_M_insert_equal(const value_type& __x);
之前说过,我们通过维护副本数来插入重复值。所以我们选择方式一。
void insert(const _Tp& v) {
// 这种写法真的不需要动脑子
auto ret = Base::_M_insert_unique(v); // ret is a pair<iterator, bool>
// 如果插入成功,说明是新值
if (ret.second) ret.first->copies_count = 1;
else ++ret.first->copies_count;
// 更新节点子树大小
// 注意,由于红黑树特殊的插入方式,每次一定要 pushup 左右儿子。
_Base_ptr x = ret.first._M_node; //之前说的,由迭代器取节点指针
while (x != root()) {
pushup(lc(x)), pushup(rc(x));
x = fa(x);
}
pushup(lc(x)), pushup(rc(x));
pushup(x);
// 确保 size() 方法正常运作
++Base::_M_impl._M_node_count;
}
erase
删除操作就要复杂一些了。
众所周知,红黑树的删除操作也是极其复杂的。
所以,我们采用惰性删除。这样只会增加时间常数,而不会使时间复杂度完全坏掉。
void erase(const _Tp& v) {
// 调用现成的函数直接找要删的值啊。
auto it = Base::find(v); // it is an iterator
// 如果要删的值不存在,find() 函数会返回结束迭代器 end()
if (it == Base::end()) return;
// 惰性删除:以前删空了就不删了,保留节点。
if (it->copies_count == 0) return;
--it->copies_count;
// 更新节点子树大小。这里没有坑了。
auto x = it._M_node;
while (x != root()) {
pushup(x);
x = fa(x);
}
pushup(x);
// 确保 size() 方法正常运作
--Base::_M_impl._M_node_count;
}
其他
查询第 k 大和查询排名的功能,完全是一般写法。在此不再赘述。
前驱和后继可以简单地这样写:
// 这里要注意 -1 、 +1 的位置。十分细节。原因请自行思考。
const _Tp& predecessor(const _Tp& v) { return kth(rank(v) - 1); }
const _Tp& successor(const _Tp& v) { return kth(rank(v + 1)); }
如果你想使用其他写法,请牢记我们使用了惰性删除。留意你的算法的正确性与时间复杂度。
总结
总代码
template<typename _Tp = int>
using rb_tree = std::_Rb_tree<_Tp, _Tp, std::_Identity<_Tp>, std::less<_Tp> >;
template<typename _Val>
struct my_tree_node {
_Val value_field;
int subtree_size;
int copies_count;
my_tree_node() : value_field() { }
my_tree_node(const _Val& __val) : value_field(__val) { }
bool operator < (const my_tree_node& __x) const { return value_field < __x.value_field; }
};
template<typename _Tp>
struct my_tree : rb_tree<my_tree_node<_Tp> >
{
typedef rb_tree<my_tree_node<_Tp> > Base;
typedef typename Base::iterator iterator;
typedef typename Base::_Base_ptr _Base_ptr;
my_tree_node<_Tp> null;
#define fa(x) ( (x)->_M_parent )
#define lc(x) ( (x) == 0 ? 0 : (x)->_M_left )
#define rc(x) ( (x) == 0 ? 0 : (x)->_M_right )
#define val(x) ( (x) == 0 ? null.value_field : iterator(x)->value_field )
#define siz(x) ( (x) == 0 ? null.subtree_size : iterator(x)->subtree_size )
#define cnt(x) ( (x) == 0 ? null.copies_count : iterator(x)->copies_count )
#define root() ( Base::_M_root() )
void pushup(_Base_ptr x) {
if (x == 0) return;
siz(x) = siz(lc(x)) + siz(rc(x)) + cnt(x);
}
void insert(const _Tp& v) {
auto ret = Base::_M_insert_unique(v); // ret is a pair<iterator, bool>
if (ret.second) ret.first->copies_count = 1;
else ++ret.first->copies_count;
auto x = ret.first._M_node;
while (x != root()) {
pushup(lc(x)), pushup(rc(x));
x = fa(x);
}
pushup(lc(x)), pushup(rc(x));
pushup(x);
++Base::_M_impl._M_node_count;
}
void erase(const _Tp& v) {
auto it = Base::find(v); // it is an iterator
if (it == Base::end()) return;
if (it->copies_count == 0) return;
--it->copies_count;
auto x = it._M_node;
while (x != root()) {
pushup(x);
x = fa(x);
}
pushup(x);
--Base::_M_impl._M_node_count;
}
const _Tp& kth(int k) {
auto x = root();
while (x) {
if ( k <= siz(lc(x)) ) x = lc(x);
else {
k -= siz(lc(x)) + cnt(x);
if (k <= 0) return val(x);
x = rc(x);
}
}
return val(0);
}
int rank(const _Tp& v) {
int res = 1;
auto x = root();
while (x && v != val(x)) {
if (v < val(x)) x = lc(x);
else { // v > val(p)
res += siz(lc(x)) + cnt(x);
x = rc(x);
}
}
return res + siz(lc(x));
}
const _Tp& predecessor(const _Tp& v) { return kth(rank(v) - 1); }
const _Tp& successor(const _Tp& v) { return kth(rank(v + 1)); }
#undef fa
#undef lc
#undef rc
#undef siz
#undef cnt
#undef root
};
例题
#include <bits/stdc++.h>
template<typename _Tp>
using rb_tree = std::_Rb_tree<_Tp, _Tp, std::_Identity<_Tp>, std::less<_Tp> >;
template<typename _Val>
struct my_tree_node {
_Val value_field;
int subtree_size;
int copies_count;
my_tree_node() : value_field() { }
my_tree_node(const _Val& __val) : value_field(__val) { }
bool operator < (const my_tree_node& __x) const { return value_field < __x.value_field; }
};
template<typename _Tp>
struct my_tree : rb_tree<my_tree_node<_Tp> >
{
typedef rb_tree<my_tree_node<_Tp> > Base;
typedef typename Base::iterator iterator;
typedef typename Base::_Base_ptr _Base_ptr;
my_tree_node<_Tp> null;
#define fa(x) ( (x)->_M_parent )
#define lc(x) ( (x) == 0 ? 0 : (x)->_M_left )
#define rc(x) ( (x) == 0 ? 0 : (x)->_M_right )
#define val(x) ( (x) == 0 ? null.value_field : iterator(x)->value_field )
#define siz(x) ( (x) == 0 ? null.subtree_size : iterator(x)->subtree_size )
#define cnt(x) ( (x) == 0 ? null.copies_count : iterator(x)->copies_count )
#define root() ( Base::_M_root() )
void pushup(_Base_ptr x) {
if (x == 0) return;
siz(x) = siz(lc(x)) + siz(rc(x)) + cnt(x);
}
void insert(const _Tp& v) {
auto ret = Base::_M_insert_unique(v); // ret is a pair<iterator, bool>
if (ret.second) ret.first->copies_count = 1;
else ++ret.first->copies_count;
auto x = ret.first._M_node;
while (x != root()) {
pushup(lc(x)), pushup(rc(x));
x = fa(x);
}
pushup(lc(x)), pushup(rc(x));
pushup(x);
++Base::_M_impl._M_node_count;
}
void erase(const _Tp& v) {
auto it = Base::find(v); // it is an iterator
--it->copies_count;
auto x = it._M_node;
while (x != root()) {
pushup(x);
x = fa(x);
}
pushup(x);
--Base::_M_impl._M_node_count;
}
const _Tp& kth(int k) {
auto x = root();
while (x) {
if ( k <= siz(lc(x)) ) x = lc(x);
else {
k -= siz(lc(x)) + cnt(x);
if (k <= 0) return val(x);
x = rc(x);
}
}
return val(0);
}
int rank(const _Tp& v) {
int res = 1;
auto x = root();
while (x && v != val(x)) {
if (v < val(x)) x = lc(x);
else { // v > val(p)
res += siz(lc(x)) + cnt(x);
x = rc(x);
}
}
return res + siz(lc(x));
}
const _Tp& predecessor(const _Tp& v) { return kth(rank(v) - 1); }
const _Tp& successor(const _Tp& v) { return kth(rank(v + 1)); }
#undef fa
#undef lc
#undef rc
#undef siz
#undef cnt
#undef root
};
my_tree<int> my;
template<typename _Tp = int>
inline _Tp read() {
register _Tp x = 0;
register bool f = false;
register char c = getchar();
while ((c<48||c>57)&&(c^'-')) c=getchar();
(c^'-') || (c=getchar(), f=true);
while (c>47&&c<58) x=(x*10)+(c^48), c=getchar();
return f?-x:x;
}
using namespace std;
signed main()
{
int n = read(), m = read();
while (n--) my.insert(read());
int last = 0, ans = 0, x, opt;
while (m--) {
opt = read(), x = read() ^ last;
if (opt == 1) {
my.insert(x);
} else if (opt == 2) {
my.erase(x);
} else if (opt == 3) {
ans ^= last = my.rank(x);
} else if (opt == 4) {
ans ^= last = my.kth(x);
} else if (opt == 5) {
ans ^= last = my.predecessor(x);
} else {
ans ^= last = my.successor(x);
}
}
cout << ans;
return 0;
}
常数略大罢了。但如果你自己写丑了,说不定比这个还慢。
本文来自博客园,作者:Gyan083,转载请注明原文链接:https://www.cnblogs.com/gyan083/p/16180729.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号