神经网络基本原理

1. 基本概念

输入 input

 (x₁,x₂,x₃)是外界输入信号，一般是一个训练数据样本的多个属性，比如，我们要预测一套房子的价格，那么在房屋价格数据样本中，x₁可能代表了面积，x₂可能代表地理位置， x₃可能代表朝向。另外一个例子是， 分别代表了(红,绿,蓝)三种颜色，而此神经元用于识别输入的信号是暖色还是冷色。

权重 weights

(w₁,w₂,w₃) 是每个输入信号的权重值，以上面的(x₁,x₂,x₃)的例子来说， x₁的权重可能是 0.92， x₂的权重可能是 0.3 ，x₃ 的权重可能是 0.06。当然权重值相加之后可以不是1 。

偏移 bias

还有个 b 是怎么来的？一般的书或者博客上会告诉你那是因为  y=wx+b， b是偏移值，使得直线能够沿  Y轴上下移动。这是用结果来解释原因，并非 b 存在的真实原因。从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值时，神经元细胞才会处于兴奋状态，这个 b 实际就是那个临界值。亦即当：

 w₁⋅x₁+w₂⋅x₂+w₃⋅x₃≥t

时，该神经元细胞才会兴奋。我们把t挪到等式左侧来，变成-t，然后把它写成  b，变成了：

 w₁⋅x₁+w₂⋅x₂+w₃⋅x₃+b≥0

于是  诞生了！

2. 神经网络的主要功能

回归（Regression）或者叫做拟合（Fitting）

单层的神经网络能够模拟一条二维平面上的直线，从而可以完成线性分割任务。而理论证明，两层神经网络可以无限逼近任意连续函数。下图所示就是一个两层神经网络拟合复杂曲线的实例。

 

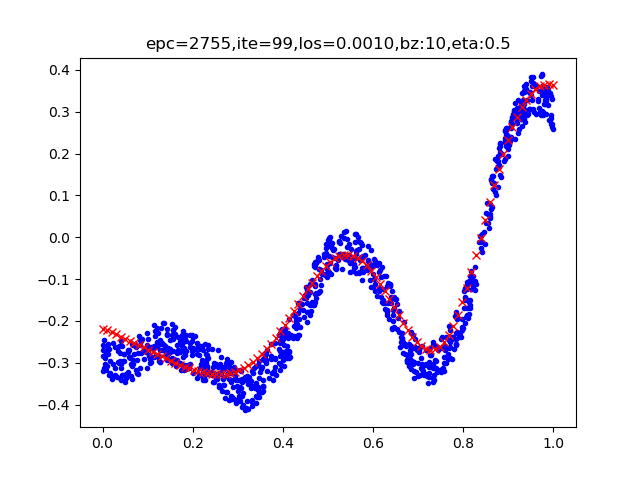
图 1回归/拟合示意图

所谓回归或者拟合，其实就是给出x值输出y值的过程，并且让y值与样本数据形成的曲线的距离尽量小，可以理解为是对样本数据的一种骨架式的抽象。

以上图1为例，蓝色的点是样本点，从中可以大致地看出一个轮廓或骨架，而红色的点所连成的线就是神经网络的学习结果，它可以“穿过”样本点群形成中心线，尽量让所有的样本点到中心线的距离的和最近。

分类（Classification）

如图2，二维平面中有两类点，红色的和蓝色的，用一条直线肯定不能把两者分开了。

 

图2 分类示意图

我们使用一个两层的神经网络可以得到一个非常近似的结果，使得分类误差在满意的范围之内。图1-19中那条淡蓝色的曲线，本来并不存在，是通过神经网络训练出来的分界线，可以比较完美地把两类样本分开，所以分类可以理解为是对两类或多类样本数据的边界的抽象。

图1和图2的曲线形态实际上是一个真实的函数在  [0,1]  区间内的形状，其原型是：

 y=0.4x²+0.3xsin⁡(15x)+0.01cos⁡(50x)−0.3

这么复杂的函数，一个两层的神经网络是如何做到的呢？其实从输入层到隐藏层的矩阵计算，就是对输入数据进行了空间变换，使其可以被线性可分，然后在输出层画出一个分界线。而训练的过程，就是确定那个空间变换矩阵的过程。因此，多层神经网络的本质就是对复杂函数的拟合。我们可以在后面的试验中来学习如何拟合上述的复杂函数的。

神经网络的训练结果，是一大堆的权重组成的数组（近似解），并不能得到上面那种精确的数学表达式（数学解析解）。

3.网络结构：分层连接

神经元被组织成不同的层（Layers）：

• 输入层 (Input Layer)： 接收原始数据（特征）。
• 隐藏层 (Hidden Layers)： 位于输入层和输出层之间，负责进行大部分的复杂计算和特征提取。深度学习中的「深」就体现在有很多隐藏层。
• 输出层 (Output Layer)： 产生最终的结果，如分类标签或预测数值。
  

神经元在层与层之间相互连接，形成一个庞大的信息处理网络。