Another Filling the Grid

Another Filling the Grid

题目信息

题目链接

Luogu CF1228E

题目描述

You have $ n \times n $ square grid and an integer $ k $ . Put an integer in each cell while satisfying the conditions below.

• All numbers in the grid should be between $ 1 $ and $ k $ inclusive.
• Minimum number of the $ i $ -th row is $ 1 $ ( $ 1 \le i \le n $ ).
• Minimum number of the $ j $ -th column is $ 1 $ ( $ 1 \le j \le n $ ).
  Find the number of ways to put integers in the grid. Since the answer can be very large, find the answer modulo $ (10^{9} + 7) $ .
  
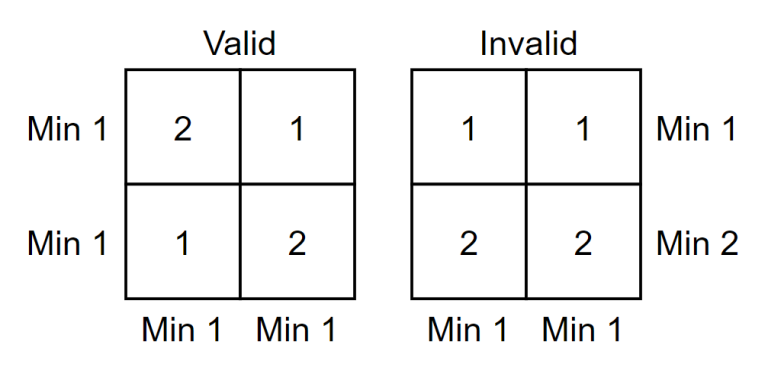
  These are the examples of valid and invalid grid when $ n=k=2 $ .

输入格式

The only line contains two integers $ n $ and $ k $ ( $ 1 \le n \le 250 $ , $ 1 \le k \le 10^{9} $ ).

输出格式

Print the answer modulo $ (10^{9} + 7) $ .

样例 #1

样例输入 #1

2 2

样例输出 #1

7

样例 #2

样例输入 #2

123 456789

样例输出 #2

689974806

提示

In the first example, following $ 7 $ cases are possible.

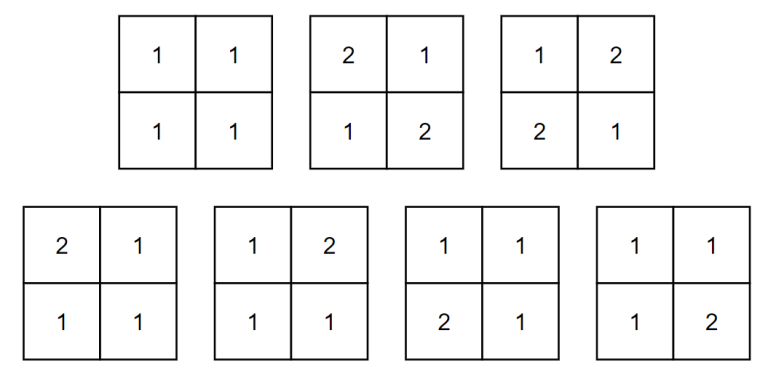
In the second example, make sure you print the answer modulo $ (10^{9} + 7) $ .

题面翻译

给定一个 \(n\times n\) 的矩阵，用 \(1\sim k\) 的数填充，每行每列最小值均为 \(1\)，问有多少填法，对 \(10^9+7\) 取模。
\(1\le n\le 250,1\le k\le 10^9\)。

思路分析

\(S_i\) 表示第 \(i\) 行不合法的方案集合。
\(T_i\) 表示第 \(i\) 列不合法的方案集合。
答案就是：\(k^{n^2}-|\displaystyle\bigcup_{1}^n S_i\displaystyle\bigcup_{1}^n T_i|\)。
\(O(2^n)\) 显然过不了，考虑优化，发现可以合并（不要只想着 1 个 \(\sum\) 的合并，要想一想多个 \(\sum\) 的合并）。
则答案为：

\[\sum_{i=0}^n\sum_{j=0}^n(-1)^{i+j}{n\choose i}{n\choose j}(k-1)^{(i+j)n-ij}k^{(n^2-(i+j)n+ij)} \]

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 2e5+10;
const int MOD = 1e9+7;
namespace math{
	int mu[MAXN],prime[MAXN];
	bitset<MAXN> is_prime;
	int frac[MAXN];
	int qpow(int a,int b){
		if(b==0) return 1;
		if(b==1) return a;
		int k = qpow(a,b>>1);
		k*=k;k%=MOD;
		if(b&1) k*=a;k%=MOD;
		return k;
	}
	int exgcd(int a,int b,int &x,int &y){
		if(b==0){
			x = 1;y = 0;
			return a;
		}
		int t = exgcd(b,a%b,x,y);
		int g = x;
		x = y;
		y = g-a/b*y;
		return t;
	}
	int inv(int a){
		return qpow(a,MOD-2);
	}
	int ex_inv(int a){
		int x,y;
		exgcd(a,MOD,x,y);
		return (x%MOD+MOD)%MOD;
	}
	int C(int n,int m){
		if(n<m) return 0;
		return frac[n]*inv(frac[m]*frac[n-m]%MOD)%MOD;
	}
	int get(int n,int m){
		return C(m+n-1,m);
	}
	void frac_init(){
		frac[0] = 1;
		for(int i = 1;i<MAXN;i++){
			frac[i] = frac[i-1]*i;
			frac[i]%=MOD;
		}
	}
	int lowbit(int k){
		return k&(-k);
	}
	int bit(int k){
		int sum = 0;
		while(k){
			sum ++;
			k -= lowbit(k);
		}
		return sum;
	}
	int log2(int k){
		for(int i = 0;i<=64;i++){
			int p = 1;
			if(p<<i==k) return i;
		}
		return 0;
	}
	void Euler_sieve(){
		mu[1] = 1;
		for(int i = 2;i<MAXN;i++){
			if(!is_prime[i]){
				prime[++prime[0]] = i;
				mu[i] = -1;
			}
			for(int j = 1;j<=prime[0]&&i*prime[j]<MAXN;j++){
				is_prime[i*prime[j]] = 1;
				if(i%prime[j]==0){
					mu[i*prime[j]] = 0;
					break;
				}else{
					mu[i*prime[j]] = -mu[i];
				}
			}
		}
	}
}
using namespace math;
int n,k,ans;
signed main(){
	scanf("%lld%lld",&n,&k);
	frac_init();
	for(int i = 0;i<=n;i++){
		for(int j = 0;j<=n;j++){
			ans += 
			qpow(-1,i+j)
			*C(n,i)%MOD
			*C(n,j)%MOD
			*qpow(k-1,(i+j)*n-i*j)%MOD
			*qpow(k,n*n-(i+j)*n+i*j)%MOD
			;
			ans%=MOD;
		}
	}
	printf("%lld",(ans%MOD+MOD)%MOD);
	return 0;
}