ABC398 E题题解

ABC398 E题题解

前言

• 个人认为这是本场比赛最难的题目。
• 交互题太烦了。

正文

什么是交互题

想要做交互题，就要先了解交互题是什么。

交互题就是你的代码和评测机进行一个游戏。

注意，这个过程是动态的。也就是你的代码输出一个，评测机就会进行响应。而我们日常的 \(\texttt{IO}\) 是这样的。

既然刚刚说了，这个过程是连续的，而你输出一个而没有达到缓冲区上限，就相当于没输出，评测机无法给出响应，你的程序就被搁置在一边，双方都在等待对方进行相应。那么我们就会 \(TLE\)。

一张梗图。。。

为了避免这样尴尬的局面发生，就需要在每次输出后清空缓冲区，让评测机进行相应。

给出这样的语句就行：

fflush(stdout);

当然，如果你是 \(cin,cout\) 爱好者，也可以使用 \(endl\)。

题面

回归正题。

思路

考虑什么样的图不会出现奇环。这一定是一张二分图，在一张二分图里面，整个图被分成完美的两部分。并且每一侧之间没有连边。

根据 \(zhx\) 的讲课，我们都知道，树一定是一张二分图。

把一棵树变成二分图的例子：

我们为了建二分图，采用染色法。

把根节点染成 \(0\)，子节点染成 \(1\)。
子节点的所有子节点都染成 \(0\)。
子节点的字节点的子节点都染成 \(1\)。

这好像非常像……

$ \color{Red} \texttt{DFS} $。

动态染色就行了。

把染成 \(0\) 的放在一边，\(1\) 的放在另一边。

根据 \(zhx\) 的讲课，我们发现，一棵树上随机连边，都会出现一个环。

那么不同颜色的点之间相互连边，就一定会出现一个偶环。

为什么呢?

因为如果是奇环，就会出现下方的局面：

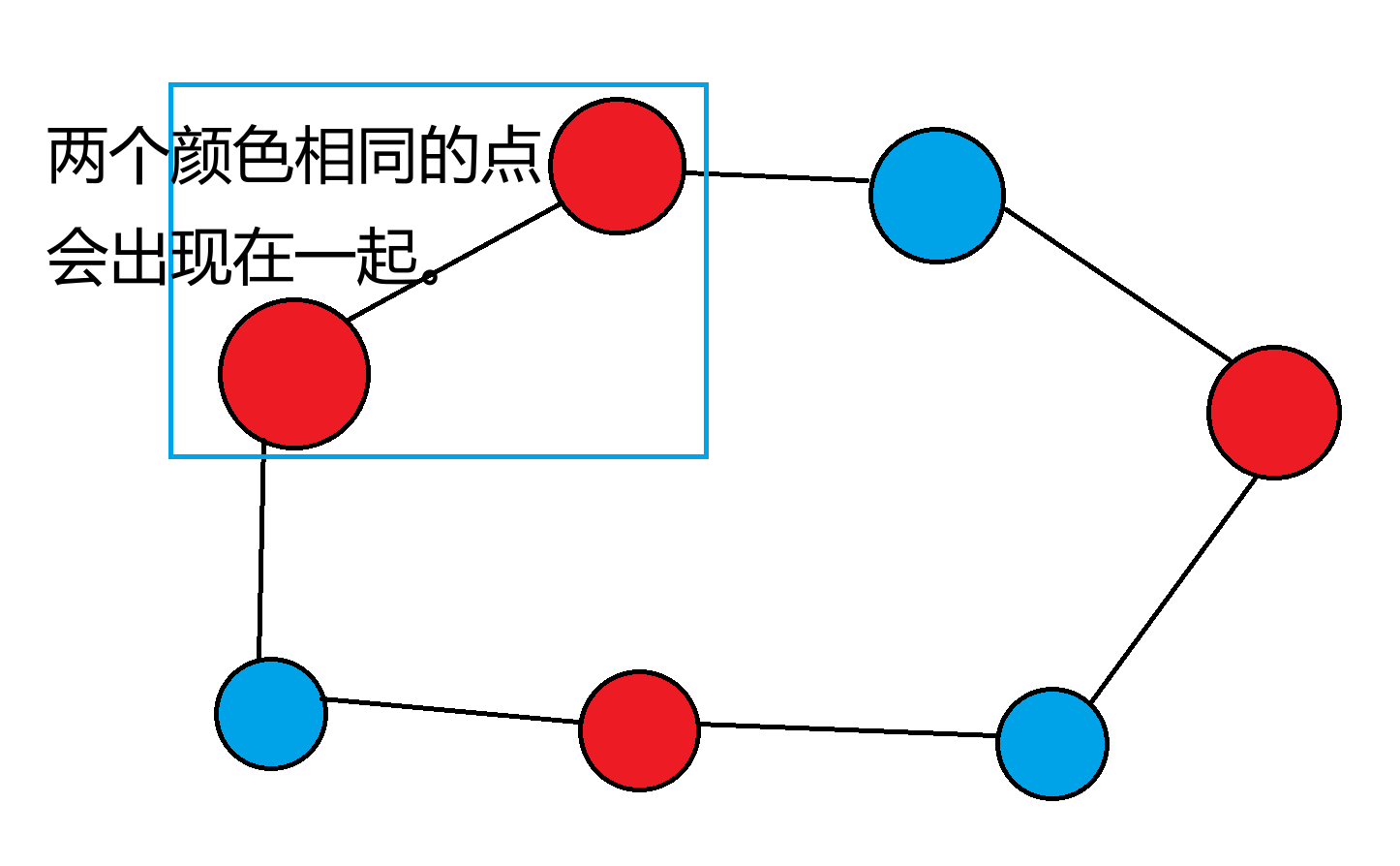
那么是不是不会产生奇环的点就是左右两边随机匹配，减去原来的边数就行了呢？

形式化的来讲，如果染成 \(0\) 的有 \(L\) 个点，染成 \(1\) 的有 \(R\) 个点，可以连的边就是：

\[L \times R - (n - 1) \]

条。

如果这个数字是奇数，就会发生这样的局面。

你选择先手，拿走第一组可以连的点
评测机选择第二组
你选择第三组
评测机选择第四组
你选择所有的奇数组
评测机选走所有的偶数组
直到……还剩下一组！！！这组的编号一定是奇数，你拿走了它……
评测机 彻底败了

如果是这个数字是偶数，就会发生相似的局面。

你选择后手
评测机选走所有的奇数
你拿走所有的偶数，因为最后一组的编号一定是偶数，所以你取走了最后一组
评测机……

总而言之，评测机怎么都会输给你。

步骤

我们发现，我们需要维护一坨点对，并且可以支持查询和删除操作。

通过我们不断的苦思冥想

\[STL-SET \]

出场了！

这个东西的内部是红黑树，具体可以看这里。

详细的步骤如下：

1. 读入
2. 染色
3. 存储不同颜色的点对
4. 如果点对数量是偶数，选择后手，否则选择先手，并且输出第一组。
5. 不断于评测机进行游戏，直到评测机彻底输掉。
6. 每输出一行，一定要刷新缓冲区！！！每输出一行，一定要刷新缓冲区！！！每输出一行，一定要刷新缓冲区！！！

代码

个人认为代码很简洁。

因为 \(n\) 只有 \(100\)，可以用最高效的邻接矩阵进行存图，查询时间复杂度 \(O(1)\)。

#include <bits/stdc++.h>

#define PII pair<int,int>

#define mkp make_pair 

#define int long long

#define il inline

using namespace std;

const int N=110;

int n;
int w[N][N];
int col[N]; 
set<PII> st;

void dfs(int now) {
	for(int to=1;to<=n;++to) {
		if(col[to]==-1&&w[now][to]) {
			col[to]=col[now]^1;
			dfs(to);
		}
	}
}

signed main() {
	cin>>n;
	for(int i=1;i<n;++i) {
		int u,v;
		cin>>u>>v;
		w[u][v]=w[v][u]=1;
	}
	memset(col,-1,sizeof col);
	col[1]=0;
	dfs(1);
	for(int i=1;i<=n;++i) {
		for(int j=i+1;j<=n;++j) {
			if(col[i]!=col[j]&&w[i][j]!=1) {
				st.insert(mkp(i,j));
			}
		}
	}
	if(st.size()%2==1) {
		cout<<"First"<<endl;
		fflush(stdout);
		auto k=*st.begin();
		cout<<k.first<<" "<<k.second<<endl;
		st.erase(k);
		fflush(stdout);
	}
	else {
		cout<<"Second"<<endl;
		fflush(stdout);
	}
	while(1) {
		int x,y;
		cin>>x>>y;
		if(x==-1&&y==-1) {
			break;
		}
		st.erase(mkp(x,y));
		auto k=*st.begin();
		cout<<k.first<<" "<<k.second<<endl;
		st.erase(k);
		fflush(stdout);
	}
	fflush(stdout);
	cout<<endl;
	return 0;
}