The First Chapter:Wave Function

Introduction to quantum mechanics

the quantum mechanics is very fascinating,no baby can truly say they really understand it,and it is counterintuitive

There were once three unuexplainable experiments

1. Blackbody spectrum
2. Photoelectric effect
3. Bright line spectra

To explore them,the scientists found the quantum mechanics

The domain of quantum mechanics

There are something different between classical mechanics and quantum mechanics

classical	quantum
certain	uncertain
predictable	predictable
determine everything	probability

When does quantum mechanics apply?

• when angular momentum \(L\)~\(\hbar\)
• when uncertainties \(\Delta p\Delta x\)~\(\hbar\)
• when uncertainties \(\Delta E \Delta t\)~\(\hbar\)
• when action \(S\)~\(\hbar\)

\(\hbar=1.05457148 × 10^{-34} kg m^2/s\)

Key concepts in quantum mechanics

The wavefunction

about its properties:

• complex function
• describe state of system
• gives probabilities

it has two part:real part of \(\psi\) and imaginary part of \(\psi\)

In math,the \(\psi^2\) is density function

In physical,the \(\psi\) is related to the probability of finding the partical at a particular point in space

Operators

it connect \(\psi\) to observables

• \(\hat{x}=x*\psi(x)\)
• \(\hat{p}=-\hbar \frac{d\psi(x)}{dx}\)

and we should know \(\hat{p}\psi\) is not "the momentum of \psi"

The Schrodinger equation

\[i\hbar \frac{\partial \psi}{\partial t}=\hat{H}\psi=(\hat{KE}+\hat{V})\psi=-\frac{\hbar^2}{2m}\frac{\partial^2 \psi}{\partial x^2}+V \]

\(\hat{H}\) is Hamiltonian energy operator

\(\\\)
the common form

\[i\hbar \frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2 \psi}{\partial x^2}+V \]

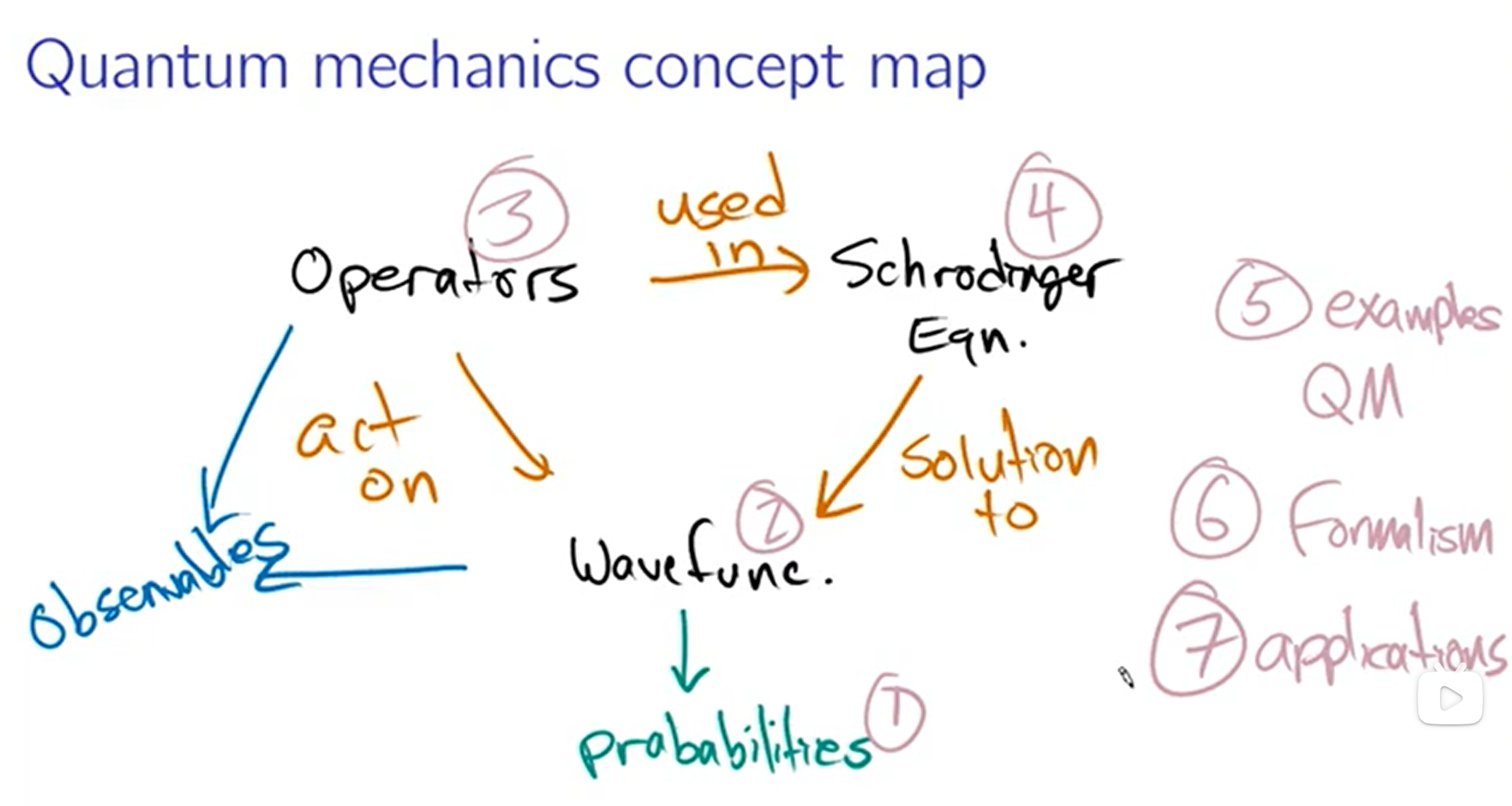
Quantum mechanics concept map

Complex number

Basic definition

complex number \(z=a+bi\)
\(i=\sqrt {-1} \\ i^2=-1\)

• the real parts \(Re(z)=a\)
• the Imaginary parts \(Im(z)=b\)

Complex exponentials

\[e^{i\theta}=cos\theta+isin\theta \]

Polar form

\[z=x+i*y=\displaystyle\sqrt{x^2+y^2}(cos\theta+isin\theta)=|z|e^{i\theta} \]

Basic operations

1. Addition (and subtraction):
   (a+i*b)+(c+id)=(a+c)+i(b+d)
2. Multiplication(distribute):
   (a+ib)(c+id)=(ac-bd)+i(ad+bc)
3. Division:
   \(\frac{a+ib}{c+id}=\frac{a+ib}{c+id}\frac{c-id}{c-id}=\frac{(ac+bd)+i(bc-ad)}{c^2+d^2}\)

The polar form obeys exponential operations as you know

Magnitudes

Complex conjugate
\((a+bi)^{*}=a-bi\)
Squared magnitude(always real,positive):
\(|z|^{2}=zz^{*}=Re(z)^2+Im(z)^2\)

Geometric interpretation

Complex plane

The complex plane has the imaginary numbers as the real numbers as the x-axis and the y-axis

for example: z=3+4i
In the complex plane,the coordinates are (3,4)
so the \(|z|=\sqrt{(3)^2+{4}^2}=5\),\(z^{*}=3-4i\) and its coordinates are (3,-4)

the polar form in complex in complex plane

\(z=Re^{i\theta}\)
\(\\\)
\(tan\theta=\frac{Im(z)}{Re(z)}\)
\(\\\)
\(R=|z|\)

Complex functions

\(f(z)=f_real (z)+f_imag (z)i=f_real(Re(z),Im(z))+if_imag(Re(z),Im(z))\)

Probability in quantum mechanics

density function p(x)

\(|\psi(x)|^2\) is a p(x) of find the particle

\(P\)(Particle is between a and b)\(=\int_a^{b}|\psi(x)|^2dx\)

but in a particular x_0 ,p(x_0)=0

what does it mean

the \(|\psi|^2\) will change after measuring

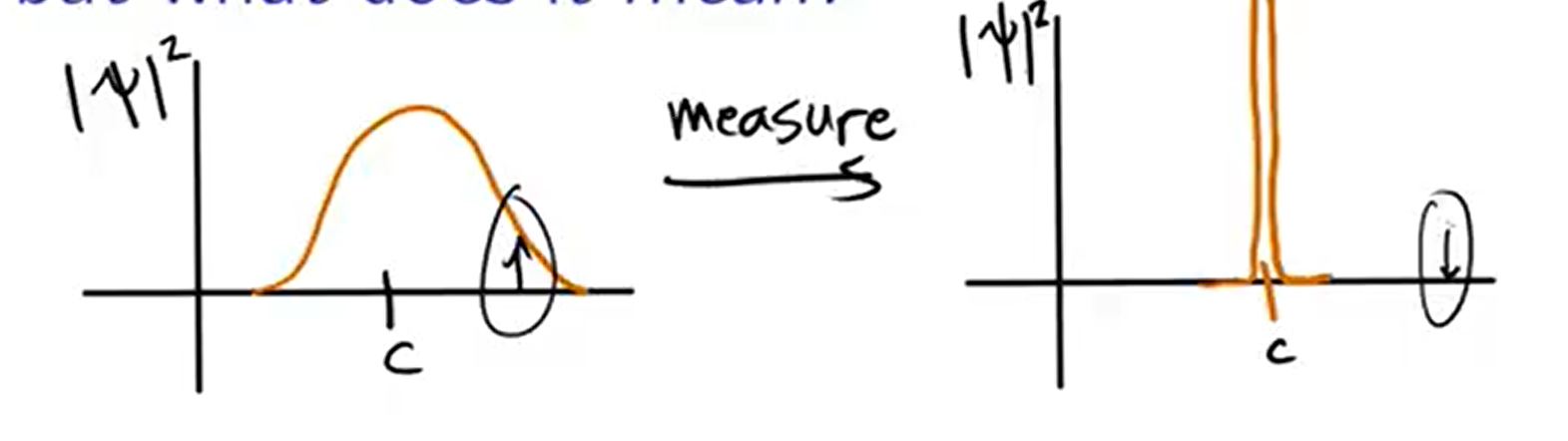
there are some interpretations about it

• the wavefunction collabses after measuring

• the particle was at c all along
  it has been proved to be wrong

• the universe split(interesting)

Probability distributions and their properties

Discrete probability

for the particular date,its probability is
the number of date/sum of number of the date

for example 1 2 3 1 2 3 3 3

the probability of 3 is \(\frac{4}{8}=\frac{1}{2}\)

most probably(mode)

Mode is the number that appears most frequently

in that example,3 is the mode

median

if the number of date is even, the median is the average of two middle value

if odd,the median is the average of the middle value

Expectation value

\[E(X)=\sum_i x_ip(x=x_i) \]

expectation value of \(f(x)\)

\[<f>=\sum_if(x_i)p(x=x_i) \]

Continuous probability

it obey the probaility density p(x),at any particular point,like p(x=1)=0

\[p(a<x\leq b)=\int_a^{b}p(x)dx \\ \int_{-\infty}^{\infty}p(x)dx=1 \]

Most prbably(mode)

in any exact value,p(x)=0,so there is no n mode

Median

\[\int_{-\infty}^{median}p(x)dx=0.5 \]

Expectation value

\[E(x)=\int_{-\infty}^{\infty}xp(x)dx \]

expectation value of f(x)
=\int_{-\infty}{\infty}f(x)p(x)dx

Variance and standard deviation

the broadness of a distribution is called the variance

\(\Delta x=x-<x>\)
\(D(x)=<\Delta x^2>=\sigma^2\)
D(x) is variance

variance formulation

variance \(D(x)\) is equal to \(<x^2>-<x>^2\)

proof:
before proof,you should know:

\(E(ax)=aE(x)\)
\(\\\)
\(E(ax+b)=E(ax)+b\)

when p(x) is discrete:

\[D(x)=E((x-E(x))^2)=E(x^2+E(x)^2-2xE(x))=E(x^2)+E(x)^2-2E(x)E(x)=E(x^2)-E(x)^2 \]

when p(x) is continous:

\[<\Delta x^2 >=\int \Delta x^2p(x)dx =\int (x-<x>)^2p(x)dx=\int(x^2-2x<x>+<x>^2)p(x)dx=\int x^2p(x)dx-\int2x<x>p(x)dx+\int<x>^2p(x)dx=<x^2>-2<x><x>+<x>^2=<x^2>-<x>^2 \]

Probability normalization and \(\psi\)

Normalization

Probability density p(x)
\(\int_{-\infty}^{\infty}p(x)dx=1\)
\(P(a<x<b)=\int_a^{b}p(x)dx\)

Wavefunction

\(\int_{-\infty}^{\infty}|\psi(x)|^2dx=1\)
\(P\)(particle is between a and b)\(=\int_a^{b}|\psi(x)|^2dx\)

to be normalizable

• \(\psi\) must be square-integrable
  \(\int_{-\infty}^{\infty}|\psi|^2dx\) is finite
• \(\displaystyle\lim_{x \to \infty} \psi=0\)

Time evolution

\(\frac{d\int|\psi(x,t)|^2dx}{dt}=\int \frac{\partial|\psi(x,t)|^2}{\partial t}dx =\int\frac{\partial(\psi ^{*}\psi)}{\partial t}dx=\int(\frac{\partial \psi*}{\partial t}\psi+\psi^{*}\frac{\partial \psi}{\partial t})dx\)

give the schrodinger equation

\[i\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial \psi}{\partial x^2}+V\psi \]

\(\\\)
so

\[\frac{\partial\psi}{\partial t}=-\frac{\hbar}{2m}\frac{\partial^2 \psi}{\partial x^2}-iV\frac{\psi}{\hbar} \\ \frac{\partial\psi^{*}}{\partial t}=-\frac{\hbar}{2m}\frac{\partial^{2} \psi^{*}}{\partial x^2}+iV\frac{\psi^{*}}{\hbar} \]

then
\( \int(\frac{\partial \psi*}{\partial t}\psi+\psi^{*}\frac{\partial \psi}{\partial t})dx=\int((-\frac{\hbar}{2m}\frac{\partial^2 \psi^*}{\partial x^2}+iV\frac{\psi^{*}}{\hbar})\psi+\psi^{*}(-\frac{\hbar}{2m}\frac{\partial^2 \psi}{\partial x^2}-iV\frac{\psi}{\hbar})dx=\frac{i\hbar}{2m}\int -\frac{\partial^2\psi^*}{\partial x^2}\psi+\psi^*\frac{\partial^2\psi}{\psi x^2}dx \)
at the end

\(\int_{-\infty}^{\infty}|\psi(x)|^2dx=\frac{d\int|\psi(x,t)|^2dx}{dt}=\frac{i\hbar}{2m}\int -\frac{\partial^2\psi^*}{\partial x^2}\psi+\psi^*\frac{\partial^2\psi}{\psi x^2}dx=\int_{-\infty}^{\infty} \frac{\partial}{\partial x}(\psi^*\frac{\partial \psi}{\partial x}-\frac{\psi^*}{\partial x}\psi)dx=\frac{i\hbar}{2m}(\psi^*\frac{\partial \psi}{\partial x}-\frac{\psi^*}{\partial x}\psi)|_{-\infty}^{\infty} \)

due to\(\displaystyle\lim_{x \to \pm\infty} \psi=0\)

\[\frac{i\hbar}{2m}(\psi^*\frac{\partial \psi}{\partial x}-\frac{\psi^*}{\partial x}\psi)|_{-\infty}^{\infty}=0 \\ \frac{d}{dt}\int_{-\infty}^{\infty}|\psi(x)|^2dx=\frac{d\int|\psi(x,t)|^2dx}{dt}=0 \]

\(\int_{-\infty}^{\infty}|\psi(x)|^2dx=constant\)
so the time evolution does not affected normalization

Motion ,repeated measurement

Can we predicat motion in quantum mechanics?
yes ,we can know how the center of probability distribution,the center of wave function move

\(<x>=\int_{\infty}^{\infty}\psi^*x\psi dx\)
then
\(\frac{d}{dt}<x>=\frac{d}{dt}\int_{-\infty}^{\infty}x\psi(x,t)^*\psi(x,t) dx=\int x\frac{\partial}{\partial t}\psi^*\psi dx=\frac{i \hbar}{2m}\int x\frac{\partial}{\partial x}(\psi^*\frac{\partial \psi}{\psi x}-\frac{\partial \psi*}{\partial x}{\psi})dx=\frac{i\hbar}{2m}(x(\psi^*\frac{\partial \psi}{\psi x}-\frac{\partial \psi*}{\partial x}{\psi})|_{-\infty}^{\infty}-\int(\psi^*\frac{\partial \psi}{\psi x}-\frac{\partial \psi*}{\partial x}{\psi})dx)=\frac{i\hbar}{2m}\int\psi^*\frac{\partial \psi}{\psi x}dx-\int\psi\frac{\partial \psi*}{\partial x}dx=\frac{\hbar}{m}\int \psi*\frac{\partial \psi}{\partial x} dx=<\hat{v}>\)

Expectation value of operators

• \(<\hat{v}>=-\frac{ih}{m}\int \psi^*\frac{\partial \psi}{\psi x}dx \)

• \(<\hat{p}>=\int \psi^*(-i\hbar \frac{\partial}{\partial x})\psi\)

• \(<\hat{x}>=\int \psi^*(x)\psi dx\)

operators:

\[\hat{x}=x*sth \\ \hat{v}=-\frac{i\hbar}{m}\frac{\partial sth}{\partial x} \\ \hat{T}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}sth \\ \]

In general

\[<\hat{Q}>=\int \psi^*\hat{Q}\psi dx \]

Q=something with \(\hat{x}\)..\(\hat{T}\)...

An introduction to the uncertainty principle

Position and wavelength

According to the Fourier transform
,$\Delta x \Delta\lambda \geq 1 $

Matter waves(Debroglie)

how do these wave come into quantum mechanics

we all know the three formulations

• \(E=mc^2\).....1
• \(E=hf\)......2
• \(c=f\lambda\).....3

if 1 and 2 describe the wave,\(mc^2=hf\)
then \(mc^2=h\frac{c}{\lambda}\)

\(mc=\frac{h}{\lambda}\)

we can consider the \(mc\) as momentum when velocity is \(c\)(c is equal to the speed of light)

so \(p=\frac{h}{\lambda}\)

it is also true for matter

Position-momentum uncertainty

through \(p=\frac{h}{\lambda},\Delta \lambda \Delta x \geq 1\)

we get \(\Delta p \Delta x \geq \frac{\hbar}{2}\)

Energy-time uncertainy

\(\Delta p \Delta x \geq \frac{\hbar}{2}\)

\(\Delta p\) is related to the wavelength,which is the frequence of wave in space
\(\Delta x\) is related to space

Make an analogy

\(\Delta E \Delta t \geq \frac{\hbar}{2}\)

$\Delta E $ is related to frequence of wave in time
\(\Delta t\) is related to time

Summary

Within the initial chapter, we obtain a fleeting view of quantum mechanics.Therefore, in the subsequent chapters, we will delve deeper into the details of it, with the aim of constructing a solid foundation in the field of quantum mechanics.