思维 / Trick 题合集

Synchronised Alpinism

别人的 30 分钟，我的一辈子。

Description

给定长度为 \(n\) 的序列 \(h\)，描述了一个山脉的形状。两个人初始时分别在 \(1\) 和 \(n\)，每时每刻都需要保证高度相等。问能否让这两个人相遇。保证 \(h_0 = h_n = 0, |h_i(1 < i < n)| \le 10 ^ 9\)

Solution

显然的，连续上升或者下降可以合并。现在可以自行思考 5min。容易发现，每次卡死的位置一定是一个这样的形状：

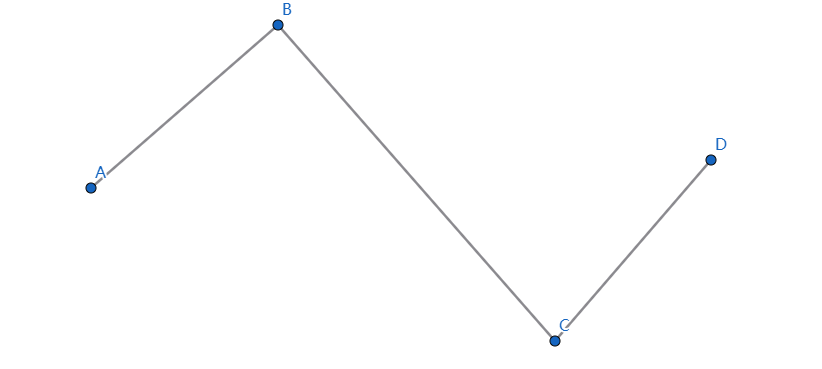
除此之外似乎无从下手。

这类题一定不能直接模拟，可以通过一些信息（充分必要的条件）来转化问题。先假设两个人可以走到的值域是 \([L, R]\)（即在这个值域内的高度可以随便走）。然么遇到一个在值域内的点直接忽略，否则如果两个高度同时在值域的一侧（上方或者下方），则将值域放大到 \(\min(h_l, h_r)\)。如果两个高度不在同一侧，则一定不合法。

抽象但是正确。感性理解吧，暂时没看到官方题解，所以不会证。

Spoj685 Seqpar

Description

将一个长度为 \(n\) 的序列 \(a\) 分成 \(m\) 段，使每一段的最大值最小。\(a\) 有正有负。

\[n, m \le 2 \times 10 ^ 5 \]

Solution

二分，朴素 DP \(f_{i, j}\) 表示前 \(i\) 个分 \(j\) 段是否合法。数据结构还要再带个 \(\log\)。爆炸。

考虑这样一件事情。如果我们能够求出合法的最小段数和最大段数，那么中间的段数一定合法吗。合法，但是我不会证。因此将 \(j\) 压进附带属性最优性 DP 就行了。

类似的，这类问题可以把限制变成求的值，验证合法性。而合法性可以通过是否在某个合法区间内来验证。而是否在每个合法区间又可以通过最优性 DP 来解决，直接压掉一维。

CF1951D Buying Jewels

Description

\(n\) 枚硬币，要恰好买 \(k\) 件物品。现在可以设置小于等于 \(60\) 个摊位，每个摊位可以设置一个价格属于 \([1, 10 ^ {18}]\)。这个人会顺序买且能买就买，硬币不一定要花完。现在要问能否构造方案，且输出方案。

Solution

\(k > n\) 不合法。\(k = n\) 就构造 \(1\)。显然不能直接构造 \(\lfloor \frac{n}{k} \rfloor\)，因为 \(\lfloor \frac{n}{\lfloor \frac{n}{k} \rfloor} \rfloor \ge k\)。对于 \(k > \lfloor \frac{n}{2} \rfloor\) 的情况来说，除了 \(n = 2k + 1\) 一定不合法。感性理解就是选 \(1\) 不够，选 \(2\) 少了。如果选了大于 \(\lfloor \frac{n}{2} \rfloor\) 的那么剩下的也不够。

对于剩下的情况，第一个定价 \(n - k + 1\), 则第二个一定剩下 \(k - 1\) 个硬币，一定合法。

关键是最大选 \(60\) 个非常迷惑人往二进制上想。

CF1991D Prime XOR Coloring

Description

构造长度为 \(n\) 的序列 \(a\)，使得对于每一个 \(i, j\)，若 \(i \operatorname{xor} j\) 为质数，则 \(a_i \not = a_j\)。

Solution

猜测颜色个数不超过 \(4\)。考虑奇偶分类，则对于奇偶性相同的数，只有二进制异或为 \(2\) 的情况才会有不同的颜色。因此考虑奇偶各开两个颜色，则对于任意奇偶之间的边，连接的两个颜色一定不同。

CF825E

Description

给定一个 DAG，给每一个点赋一个权值 \(a_i\)，且 \(a\) 是排列，要求对于边 \(u \to v\)，满足 \(a_u < a_v\)，满足 \(a\) 字典序最小。

Solution

有一种很显然的贪心：正着做，每次给可以处理的编号最小的点赋值。但是这样做是错的。因为可以先给一个编号更大的点赋值，然后它后面藏着一个编号更下的点。也就是说这么做是有后效性的。

考虑反过来做，建反图，每次从编号最大的点赋最大的值，证明可以看尺子姐姐的证明。

附赠一道题：AT_arc200_c。