线段树-基础

1.引语

线段树，可谓是好用的数据结构（废话）

2.线段树作用

1. 区间加和
2. 区间查找
3. 区间最大值，最小值。。。
4. 数据结构优化，配合如树链剖分解决问题

3.线段树概念：

存储：

线段树需要用结构体存储
代码：

struct tr{
    int l,r;
    long long sum,lazy;
}t[N<<2];

其中，\(sum\) 代表该节点维护的值，\(l，r\) 代表该节点维护的区间范围，\(lazy\) 为懒标记,其余也可以通过增加数组来维护。

建树

一个节点 \(node\)，它的左儿子的编号为 \(2*node\)，右节点为 \(2*node|1\)。
其中，树的每个没有子节点的节点就是放置数组 \(a\) 的。

而每个根节点都是放置其两个子节点的某些特性（如加和，最大值，最小值....）

树状数组的建树图像可以看成是这样：

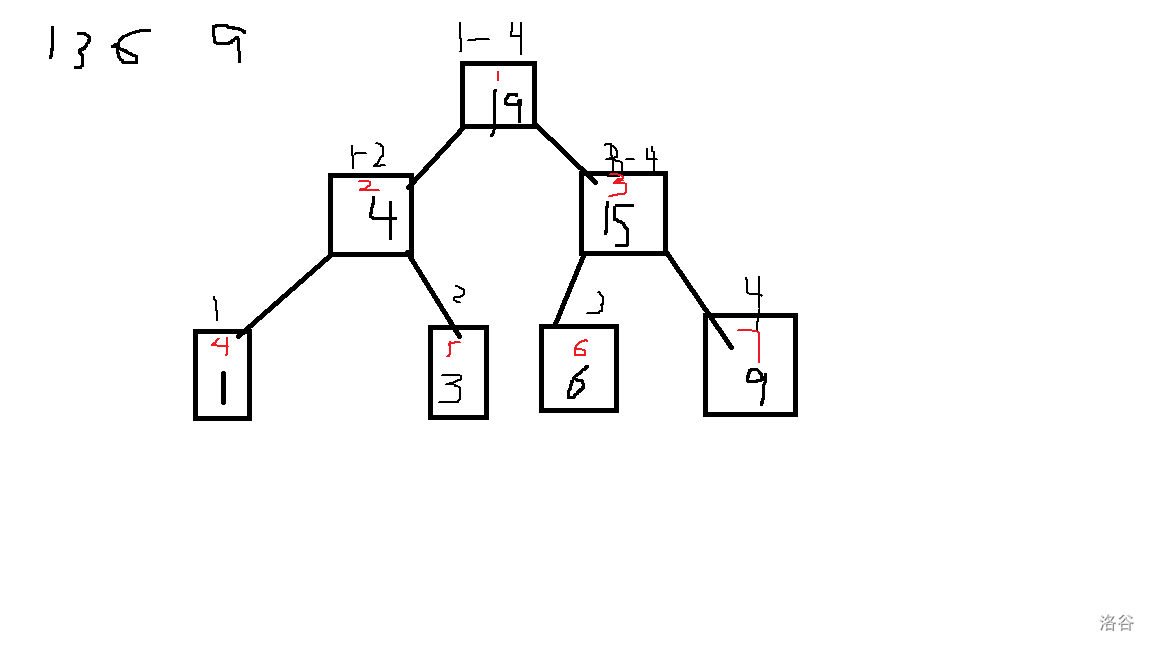
当左区间和右区间所划定的范围相同，

也就是其为子节点，
那么就可以将 \(a\) 数组中对应的数值赋值到 \(sum\) 中。下面是代码：

void build(int x,int l,int r)
{
    t[x].l=l,t[x].r=r;//设立p点所对应的区间范围为l-r
    if(l==r){
        t[x].sum=a[l];
        return;
    }
    int mid=l+r>>1;//取中点
    build(x<<1,l,mid);//左子树，编号为p*2，范围为 l-mid
    build(x<<1|1,mid|1,r);//右子树，编号为p<<1+1，范围为mid+1—r
    t[x].sum+=t[x<<1].sum+t[x<<1|1].sum;//p点的值为左右两个子书节点的值的和
   	
}

区间查询：

查询的思想是这样：假如说要求取 \(1-3\) 的加和，
根据上面的图来看，首先从根节点开始找，分成\(1-2,3-4\)。
而此时我们发现，\(1-2\) 正好包括在 \(1-3\) 中，那么直接返回值，
接着，由于 \(3-4\) 不在范围内，继续往下分为\(3,4\), \(3\)在范围内，直接返回三。
运用到代码中长这样：

long long ask(int x,int l,int r)
{
    if(l<=t[x].l&&r>=t[x].r)//在范围内
        return t[x].sum;//直接返回值
    else if(t[i].r<l||t[i].l>r) return 0;//这个区间和目标没有关系，即在目标之外，直接返回0
    int mid=t[x].l+t[x].r>>1;
    long long ans=0;
    if(l<=mid)  ans+=ask(x<<1,l,r);//如果这个区间的左儿子与目标区间有交集，那么搜索。
    if(r>mid) ans+=ask(x<<1|1,l,r);//如果这个区间的右儿子与目标区间有交集，那么搜索。
    return ans;
}

单点修改

算法的目标是在 \(pos\) 的位置上加上一个\(k\)。

从根节点开始，看这个\(pos\)是左儿子还是右儿子。

比较好理解，因此直接上代码：

void add(int x,int k,int pos)
{
    if(t[x].l==t[x].r)//如果这个区间被完全包括在目标区间里面，那么就直接添加赋值 
    {
        t[x].sum+=k;
        return;
    }	
    if(pos<=t[x<<1].r)  add(x<<1,k,pos);//dis的区间判断 
    else add(x<<1|1,k,pos);
    t[i].sum=t[x<<1].sum+t[x<<1|1].sum;//回溯时需要重新赋值 
}

区间修改

思路：如果把这个区间加上\(k\)，相当于在这个区间上涂上一个\(k\)的标记，单点查询时就把标记加上即可。

int add(int x,int l,int r,int k){
    if(t[x].l>=l&&t[x].r<=r){//如果这个区间被完全包括在目标区间里面，讲这个区间标记k
        t[x].num+=k;
        return 0;
    }
    if(t[x<<1].r>=l)  add(x<<1,l,r,k);//左子树的右区间的边界小于左边界
    if(t[x<<1|1].l<=r)  add(x<<1|1,l,r,k);//右子树的左边区间小于右边界 
} 

单点查询

\(pos\) 去哪，把路径上所有值加起来就好。

void search(int x,int pos)
{
    ans+=t[x].num;//一路加起来
    if(t[x].l==t[x].r)  return;
    if(pos<=t[x<<1].r)  search(x<<1,pos);
    if(pos>=t[x<<1|1].l) search(x<<1|1,pos);
}

至此，线段树基础部分完结