【NOI2019】序列 题解（贪心模拟费用流）

（感觉是有史以来自己代码最好看的一次

贪心模拟费用流。

LG传送门

Solution

1

经过一番思考，不难发现我们可以根据题面建图跑费用流。具体见下图：（从@cmd大佬那里薅来的。）

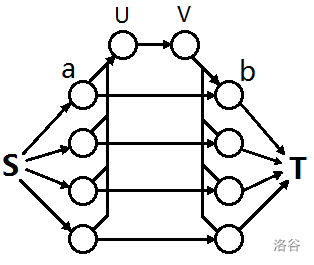
然后你可以跑一发费用流，然后成功 \(\text{T}\) 掉。

2

“如何提高费用流效率？我们有个叫“模拟费用流”的东西。说白了，我对模拟费用流的理解就是，在特殊条件允许下，用贪心来取代spfa找最短路，用各种手段（代价取反、分类讨论等等）来模拟退流过程。”（from @wyt2357）

不难发现，在可行的情况下，走 \(UV\) 这条路径总是最优的，因为它不受“\(a,\ b\)下标一样”的限制。故我们不妨在 \(a,\ b\) 各挑 \(K-L\) 个最大权值，即经过 \(UV\) 这条边能获得的最大总权值。此处涵盖一个巧妙的转化：将“至少 \(L\) 对下标相同”转化为“至多 \(K-L\) 对下标不同”，简化了模拟费用流。另：若对于某一下标 \(i\)，\(a_i\) 和 \(b_i\) 都被选中，那么就可以不经过 \(UV\)，走 \(S\rightarrow a_i\rightarrow b_i\rightarrow T\) 这条路径。记 \(cnt\) 为满足上述条件的、不同的 \(i\) 的个数。

故对这 \(cnt\) 条边，我们可以统计进 \(L\) 中。所以，我们还需要找 \((L-cnt)+cnt=L\) 条路径。前者是不经过 \(UV\) 的路径个数，后者相反。

---

我们优先统计 \(cnt\) 条经过 \(UV\) 的路径。此时 \(a,\ b\) 下标可以任意选，所以选择剩余节点中权值最大的即可。若两者下标不同，\(cnt\) 则减 \(1\)；反之，不变。故这里需要两个堆，\(h_1,\ h_2\)，分别记录 \(a,\ b\) 中没使用过的权值（记 \(A\) 为选中的 \(a_i\) 权值的集合，\(B\) 同理）：

• \(h1\)：对于 \(i\in h1\)，满足 \(a_i \notin A\)；
• \(h2\)：对于 \(i\in h2\)，满足 \(b_i \notin B\)。

---

而在统计不经过 \(UV\) 的路径时，我们需要三个堆去记录：

• \(f1\)：对于 \(i\in f1\)，满足 \(a_i \notin A\ \land b_i \in B\)；
• \(f2\)：对于 \(i\in f2\)，满足 \(a_i \in A\ \land b_i \notin B\)；
• \(h3\)：对于 \(i\in h3\)，满足 \(a_i \notin A\ \land b_i \notin B\)。

而三个堆对应着三种路径情况：

1. 对于 \(i\in f1\)，必定存在路径 \(S\rightarrow a_j \rightarrow b_i \rightarrow T\)，则我们可以从 \(h2\) 中选出 \(l\)，满足 \(b_l\) 在 \(h2\) 中最大。如此可使上述路径转化为路径 \(S \rightarrow a_j \rightarrow b_l \rightarrow T\) 和路径 \(S \rightarrow a_i \rightarrow b_i \rightarrow T\)。
2. 对于 \(i\in f2\)，构造方法同上。
3. 从 \(h3\) 中挑选 \(i\)，满足 \(h3\) 中 \(a_i+b_i\) 最大。故可构造路径 \(S \rightarrow a_i \rightarrow b_i \rightarrow T\)。

对与第一或第二种构造方式，可能会出现 \(j=l\) 的情况，此时我们会多构造出一条不过 \(UV\) 的路径，所以我们就优先选择这样走，可使得 \(cnt+1\)，更优。所以需要特判一下选择那种构造方式。当不存在上述特殊情况时，直接选择贡献最多的方式即可。

---

\(\text{BTW}\)，时复 \(\mathcal{\text{O}}(n\log n)\)。

Code

u1s1，看起来整齐且短。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
#define per(i, a, b) for(int i = a; i >= b; --i)
#define h1p h1.top().id
#define f1p f1.top().id
#define h2p h2.top().id
#define f2p f2.top().id
#define h3p h3.top().id
const int maxn = 2e5 + 5;
int T, n, L, K;
int v1, v2, v3, vmx;
int a[maxn], b[maxn], s[maxn], c[maxn];
ll ans; int cnt; 
struct node1{ int id; 
	bool operator <(const node1 x) const{return a[id] < a[x.id];}
}t1; priority_queue<node1> h1, f1; 
struct node2{ int id; 
	bool operator <(const node2 x) const{return b[id] < b[x.id];}
}t2; priority_queue<node2> h2, f2;
struct node3{ int id; 
	bool operator <(const node3 x) const{return a[id] + b[id] < a[x.id] + b[x.id];}
}t3; priority_queue<node3> h3;
inline bool cmpa(int x, int y){return a[x] > a[y];}
inline bool cmpb(int x, int y){return b[x] > b[y];}

inline void init(){
	while(h1.size())h1.pop(); while(f1.size())f1.pop();
	while(h2.size())h2.pop(); while(f2.size())f2.pop();
	while(h3.size())h3.pop();
}
inline void init2(){
	while(h1.size() and (s[h1p] != 2 and s[h1p] != 0)) h1.pop(); 
	while(f1.size() and (s[f1p] != 2)) f1.pop();
	while(h2.size() and (s[h2p] != 1 and s[h2p] != 0)) h2.pop(); 
	while(f2.size() and (s[f2p] != 1)) f2.pop();
	while(h3.size() and (s[h3p] != 0)) h3.pop();
}
inline void slv(){ init(); ans = cnt = 0;
	scanf("%d%d%d", &n, &K, &L);
	rep(i, 1, n) scanf("%d", &a[i]); rep(i, 1, n) scanf("%d", &b[i]);
	rep(i, 1, n) c[i] = i, s[i] = 0;
	sort(c + 1, c + n + 1, cmpa); rep(i, 1, K - L) s[c[i]] += 1, ans += a[c[i]];
	sort(c + 1, c + n + 1, cmpb); rep(i, 1, K - L) s[c[i]] += 2, ans += b[c[i]];
	rep(i, 1, n) if(s[i] == 3) cnt += 1;
		else if(s[i] == 2) t1.id = i, h1.push(t1), f1.push(t1);
		else if(s[i] == 1) t2.id = i, h2.push(t2), f2.push(t2);
		else t1.id = t2.id = t3.id = i, h1.push(t1), h2.push(t2), h3.push(t3);
	//---
	while(L--){ init2();
		if(cnt){ cnt -= 1; int i = h1p, j = h2p;
			ans += a[i] + b[j], s[i] |= 1, s[j] |= 2;
			if(i == j){cnt += 1; continue;}
			if(s[i] != 3) t2.id = i, f2.push(t2); else cnt += 1;
			if(s[j] != 3) t1.id = j, f1.push(t1); else cnt += 1;
			continue;
		} vmx = v1 = v2 = v3 = 0; int i, j;
		if(f2.size()) i = h1p, j = f2p, v1 = a[i] + b[j];
		if(f1.size()) i = f1p, j = h2p, v2 = a[i] + b[j];
		if(h3.size()) i = h3p, v3 = a[i] + b[i];
		vmx = max(v1, max(v2, v3)), ans += vmx;
		if(v1 == vmx and ((v1 == v2 and s[h1p] != 2) or v1 != v2)){
			s[h1p] |= 1, s[f2p] |= 2;
			if(s[h1p] != 3) t2.id = h1p, f2.push(t2); else cnt += 1;
		} else if(v2 == vmx and ((v1 == v2 and s[h1p] == 2) or (v1 != v2))){
			s[f1p] |= 1, s[h2p] |= 2;
			if(s[h2p] != 3) t1.id = h2p, f1.push(t1); else cnt += 1;
		} else i = h3p, h3.pop(), s[i] = 3;
	} printf("%lld\n", ans);
}

int main(){
	scanf("%d", &T); while(T--) slv();
	return 0;
}

---

end.