CF 比赛整理合集

Codeforces Round 801 (Div. 2)

B. Circle Game

博弈/必胜策略题。探究奇偶关系。

• 发现谁有必胜策略与当前堆的数量有关系。若数量为偶数，那么这两个人各取各的，互不影响，此时就看谁取的堆中的石子最小值小了。
• 反之，若为奇数，举例有 3 堆，那么第一个人取的堆数是：1、3、2、1...，第二人的是：2、1、3、2...发现第二个人在第二次会取到第一堆，所以只要第一个人第一次把第一堆取完，第二人必输。

C. Zero Path

奇偶判定 + 简单 dp + 推结论。

首先，要发现走完全程会走 \((n+m-1)\) 个格子，每个格子权值非 1 即 -1，为最后和为 0，故 \((n+m-1)\) 需是 2 的倍数。直觉和 dp 有关，但是直接暴力 dp 肯定会挂空间，除非使用 bitset。

虽然不能全部 dp 求出，但我们可以在复杂度允许范围内求出从头走到尾获得总和的最大值 \(mx\) 与最小值 \(mn\)。而要想最后和为 0，必须满足 \(mn\leq 0 \leq mx\)。为什么满足这个不等式就说明最终和为 0 可以实现呢？因为我们在之前已经保证了 \((n+m-1)\) 的奇偶性，所以 \(mx\) 和 \(mn\) 必定都为偶数，而通过拐角的不同走法可以对这两条路径的权值和进行加二或减二操作，故可以实现。更严谨的证明。

My submission.

Codeforces Round 875 (Div. 2)

Written Time：2023年5月30日

D. The BOSS Can Count Pairs

发现 \(a_i,\ b_i\) 的值域与 \(n\) 同级。所以从值域的角度出发考虑问题。

发现可以直接枚举 \(a_j\) 的大小，并且这个大小是不超过 \(\sqrt n\) 的。然后再去寻找对应的合法的 \(b_j\)。

这样一来 \(O(n^2)\) 的暴力就能被优化到稳定的 \(O(n\sqrt n)\)。可过。

My submission.

E. Hyperregular Bracket Strings

显然括号序列的方案数可以使用卡特兰数 \(O(n)\) 预处理。

考虑区间交的情况。那么我们可以把这两个相交的区间拆分成三份，首一份、重叠的一份、尾一份。

然后中间重叠的这一份一定是一个完整的括号序列，其方案数是可以直接求出来的。

经过简单推论，首一份与尾一份合起来（即不考虑中间重叠的一份）是一个完整的括号序列，其方案数亦可直接求出。

同时，易证这两个完整的括号序列是互不干扰的。

区间不相干的时候方案当然独立，直接方案数相乘即可。区间包含的时候和区间相交的情况同理。

所以，假设覆盖点 \(i\) 的区间的集合为 \(S_i\)，易知所有 \(S_i\) 相同的数实际上是构成一个完整的括号序列的。

所以最终的答案就是所有 \(S_i\) 对应的括号序列方案数相乘取模即可。

维护这个 \(S_i\) 相同的点，我们使用一个类似哈希的小技巧。它满足溢出之后依旧满足哈希性质。注意取 rand() 的时候要平方，因为 \(n\) 比较大。

My submission.

Codeforces Round 880 (Div. 2)

Written Time：2023年7月12日

D. Lottery

想出来了一半吧。主要是自己在思考的时候思路比较凌乱，而且没能很好地将思路和实现联系起来思考。

我们能够很显然地发现对于一个数 \(x\)，能够覆盖它的合法 \(target\) 值的范围是一个区间。而因为我们的编号是 \(n+1\) 所以直接考虑严格包含即可，计算出左右边界并不十分难。需要注意的一点是：主人公的数可以不是 \(a_i\)。所以我们考虑哪些值可能产生贡献（因为 \(m\) 范围太大了）。根据我们推出的左右边界的式子可以知道：\(a_i\) 和 \(a_{i+1}\) 之间的数的答案基本相同，而因为上取整所以存在一个奇偶的差别，所以分别考虑所有的 \(a_i-1,a_i-2,a_i,a_i+1,a_i+2\) 的左右边界构成的区间长度大小即可。

附详细题解：

My Submission.

Codeforces Round 889 (Div. 2)

赛时被打爆了/ng。

All my submissions. 懒得贴了，直接找吧。

C2. Dual (Hard Version)

考场上想出来了，但脑子依托答辩写挂了。

考虑优化统一正负的次数。发现当这个序列正负两两对半开的时候上面那个做法仍然可行。考虑极端情况，如果有 n-1 个 1 和 1 个 -20，直接用 -20 去统一正负是不可行的。然后把目光放到条件“-20 <= a[i] <= 20”以及“可以自己加自己”，简单推算可以发现，0 不用管，±1 如果自己加自己，最多 5 次就可以把自己加到比其他任何数都大。这么一来，对于上述极端情况，我们就可以这样做。

最后你会发现那个次数上界是出题人精心设计的上界。最多次数恰恰好是 31。

D. Earn or Unlock

想出来了一半 x 2。

发现对于解锁数量 x，我们可以直接计算贡献。然后就可以使用 bitset 优化背包去 dp 能否构造出恰好解锁 i 张卡牌的情况。然后注意 dp 要开到 n 的两倍。

但是我还是搞不明白为什么每次要对 dp[i] 清 0。摆。

Codeforces Round 676 (Div. 2)

Written Time：2023年8月9日。

VP 了个三年前的场子。主要是看到 676 是个好数就打了，遗憾的是没有 Div.1，没有 F。

VP 顺利得流泪（10:10 分开打）；2 min 切 T1 很高兴很开心；做题的时候一半的时间都花在读懂题目，非常恼火。

还是一样懒得贴链接，直接找吧。All my submissions.

D. Hexagons

模拟题 / 最短路题。

赛时没过，谁让我打到一半去睡觉呢。有三种方法，其中每一种方法我都一定程度上想到了。这里都说说吧。

Useful Observations and Notice：首先因为要求代价最小，所以我们不会同时走相反的路径，比如右上和左下；这个六边形显然可以转化成网格，除了四联通之外加上右上左下两个方向；题目问题是在坐标系上进行的，所以上下左右不能直接从网格挪过来，会反；最终最佳方案一定最多只涉及两种方向。

Method 1：暴力直接贪心分讨。根据第一条性质，我们可以推断最终一定只使用了两种方向去走。比如说当 \(x\geq 0,y\geq 0\) 时，有且仅有三种可能产生贡献的方案：横纵各自单独增；横纵同时加到较小值，剩下那个自己加；横纵同时加到较大值，剩下那个自己减。所以直接分四种情况讨论最小值即可，总共 12 条式子，并不是很复杂。Code.

为什么我全部想到却没有去写这个简单分讨呢？我也不知道自己抽什么风想到了却不写。

Method 2：我们可以根据它在水平方向、竖直方向、斜线方向行走的路程（矢量）列出三者关于 \((x,y)\) 的等式。然后很重要我没想到的一点就是，费用是常量，路程是变量，总费用是三个费用乘以三个路程之和，而三个路程都可以转化成 一个变量 与 常量 运算的等式。所以，总费用的形式是三个一次函数之和，形如 \(k_1(a_1+c_1)+k_2(a_1+c_2)+k_3(a_1+c_3)\)，其中 \(a_1\) 是水平方向上的路程。因为 \(a\) 与不同参数运算的正负性可能随着 \(a\) 的取值发生改变，所以我们不妨理解为上面这个函数是一条由多个一次函数组合而成的折线。所以极值一定只在端点取到，我们枚举 \(a\) 的三个取值 \(-c_1,-c_2,-c_3\) 即可。Solution & Code.

为什么我很接近却棋差一招呢？因为我把它拆开来了，没有观察到极值一定出现在某一项为 0 的时候。主要还是写挂了没调出来。

Method 3：我一开始也观察出来对于每个方向，使用它是有条件的。比如说右上方向，我们选择它当且仅当其代价小于先右后上的代价和。所以我们可以联系最短路，对于每个方向，我们使用 Bellman-Ford 求最短路的过程让它们自行松弛对方，当次数大于总边数的时候能够保证都松弛到最多解（这里取 10 次）。这样每个方向的代价都是按这个方向走的最小代价。然后就可以直接无脑计算总花费了。Code.

为什么我想到方向代价之间的更新却没想到这么做呢？因为我基础不好脑子不好使感觉互相更新很复杂。

总而言之就是，这题并不难，我思维太分散导致这里一点那里一点，最后没有一条路是走通了的。还有一点就是，我前面很大部分时间都读错题了，把它转化到方格上就套了 dp 去思考，右上搞成右下，没发现方格和坐标系上横纵坐标的加减是不一样的。最后就是我做到一半困死了滚去睡觉了浪费了二三十分钟。

收获就是，自己深入思考过的题，重新订正收获确实很大，能够找到自己的思维误区和改进之处，对题目的思考也更加深入透彻。

E. Swedish Heroes

找规律 + 线性 dp。

本来不想做了，看到 jy 做了还水了篇题解，就看题解做掉了。

简化一下题目，把式子拆开来，就会发现它实际上就是给一个序列赋上正负号求值，符号顺序你定，使得最终值最大。这个很显然用 dp 做嘛。因为是合并相邻项所以使用经典的模型区间 dp 去做，转移式也很好推，问题就是复杂度飙到 n^3 跑不了。发现难点在于符号定序如果想要线性去做，我们就需要得到它的充要条件。

然后，人有多大胆，结论多好用。

你就枚举不同序列长度的情况下不同的正负号序列然后暴力找规律猜结论。然后得到：记负号数量为 \(p\)，正号数量为 \(q\)，那么一个必要条件是 \(2p+q\equiv 1\pmod 3\)。可以用数学归纳法去证，证明见最后 Solution 里面。然后考虑充分性，会发现有一个《corner case》是阿巴阿巴……，我也不知道怎么保证的充分性，结果就是要再考虑是否存在相邻同正负的情况，如果不存在即不合法。这个结论本身手玩小样例就可以得到，比较显然。

然后就可以用一个简单线性 dp 去做啦。

写的很糙，还是看比较严谨的 Solution 吧（虽然他也没说怎么保证的充分性）。

Codeforces Round 892 (Div. 2)

Written Time：2023年8月19日。

省流：赛时打的很满意。

好困啊，就跑过来补一下之前欠下的场子。洛谷的题解写的都很不错了。

All My Submissions.

D. Andrey and Escape from Capygrad

简单题。

比较 shaber 的一道题，也不能算贪心，顶多算个结论题。赛时没调一发过。我的评价是不如 C。

这就是西埃弗 *1800 吗。看到这个区间快乐跳，很显然就要分析它的用处和性质了。我们不妨把它分为三部分：左区间、中区间、右区间。最特殊的当然是右区间往左区间跳了。

不妨分析右区间的点 \(x\) 在什么情况下会选择跳到中区间。原因肯定是中区间的点 \(y\) 一定能够跳到一个大于 \(x\) 的位置 \(z\)。但是这个时候我们会发现，如果说 \(y\) 能够跳到 \(z\)，说明 \(z\) 最多就是某一个区间中区间的右端点。而我们又有：只有左区间和中区间的点能在当前区间往右跳，且最多跳到中区间的右端点。那么，如果 \(y\) 能到 \(z\)，\(x\) 一定也能到 \(z\)。所以，对于右端点的点，这个区间的快乐跳权力，对它们而言根本没必要。

所以题目就转化为给一堆区间，且这些区间里面的点都可以跳到这个区间的右端点。那么这个时候显然对于区间包含、区间相交而言，都是可以直接合并的。

那么做法就太显然了。区间排序然后区间合并，查询的时候直接二分一下最大合法右端点即可。如果没有被任何区间覆盖，就只能停留在原地咯。实现起来也根本没难度。

所以，官解的那个扫描线做法真的是认真的吗？雾。

E. Maximum Monogonosity

绝对值 dp。

要吃饭了，就草草写了吧，有一篇还不错的题解。

赛时想到了 dp 转移式，但是发现这个绝对值好恶心复杂度太高剩余时间不够就没写也没想优化了。转移式很显然啊，\(f_{i,j}\) 表示前 \(i\) 个总长度为 \(j\) 的最大贡献和。考虑这个绝对值怎么转移。发现绝对值一共有 2 x 2 = 4 中形态，每次只需要取最大值即可。考虑怎么维护每一种形态的转移。发现我们可以把所有的、可能转移点的贡献边扫边维护，然后就可以 \(O(1)\) 转移了。使用到了一个小 trick：不论怎么添加区间，\(i,j\) 的差一定是不变的。这样就可以维护合法转移点的贡献了。
哦对了我懒得写了直接交了一发 std。

总结一下绝对值问题的几个解题方向：

• 假定有序，正反做两次。
• 拆开几种情况分别统计，再取最大值。
• 平方后维护。
• 对于简单题，你当然可以选择直接使用 abs()。

其实本质思路都是一样的：转化成常见的四则运算再去直接维护，宁可多次，也不在过程中添麻烦。

写飘了，言语可能比较抽象，凑合吧。

Codeforces Round 807 (Div. 2)

Written Time：2023年11月7日。

出于对时间方面的考虑，只记录一些有意义的题目。

All My Submissions.

D. Mark and Lightbulbs

观察性质 + 模拟。

一眼读题，显然发现操作类似是两个相邻的、大小不为 1 的 01 块“吃对方的点”。然后我脑子抽风不知道怎么想歪的，没有从宏观角度观察序列变化。正解是考虑不论怎么变化，01 块的个数及排布方式是不变的，只有长度会变化，所以操作总次数就是每个块的变化长度之和。无解时当且仅当 \(a_1\ne b_1\) 或 \(a_n \ne b_n\)。

E. Mark and Professor Koro

线段树二分。

连最基本的类进位性质都没看出来，废了。发现可以直接对序列不断往上合并，满足合并之后 \(cnt_{a_i}\) 都满足不大于 \(1\)。然后考虑更改一个数，包括增加一个数和删除一个数。二者类似，此处只考虑增加一个数。若 \(cnt_x=0\)，表示有偶数个 \(x\)，那么直接 \(cnt_x=1\) 即可；否则会发生一系列“进位”，即记 \(x\) 之后第一个为 \(0\) 的值为 \(res\)，那么区间赋值 \(cnt[x,res-1]=0,cnt[res]=1\) 即可。关于找 \(res\)，线段树二分可做到 \(O(n\log n)\)，线段树优化二分可做到 \(O(n\log^2 n)\)。

关于线段树二分，有个结论是同一层访问的区间个数不超过 \(4\)。
实现方式理论正确，怎么都调不出来，极恼，直接交 std 了。

Codeforces Round 809 (Div. 2)

Written Time：2023年11月8日。

哈哈模拟赛结论签到题没做出来，2h 摆烂无果跑来 VP。

总结一下：A 无脑取 min，B 可爱线性 dp，C 可爱线性 dp，D1 经典确定左端点求最小右端点值。

All My Submissions.

D2. Chopping Carrots (Hard Version)

数论分块 + 双指针。

一眼数论分块，然后就啥也不知道了。根据 D1，知道对于一个合法的区间 \([l,r]\)，有 \(\forall b_i=\left\lfloor\frac{a_i}{p_i}\right\rfloor \in [l,r]\)。而等式右侧让我们想起整除分块 \(\sum \left\lfloor\frac{n}{i}\right\rfloor\) 的形式，所以一种暴力的做法是单次 \(O(\sqrt n)\) 求出 \(a_i\) 的所有可能 \(b_i\) 并存入 vector，\(O(n\sqrt n)\) 预处理，每次双指针扫判断是否每个 \(i\) 都有 \(b_i\in [l,r]\)，复杂度 \(O(n\log n)\)。

Note the unusual memory limit. 所以不能将 \(i\) 所有的 \(b_i\) 都存下来。但是根据整除分块的实现形式，\(b_i\) 是可以线性递推维护的。具体地，由于在整除分块中我们从小到大推得 \(l,r\) 的值，所以此时为了保证整除分块边界的递增性，考虑让双指针 \(L,R\) 倒序扫描。在移动左右指针时，同时维护 \(q[x]\) 存放所有满足存在 \(p_i\) 使得 \(b_i=x\) 的下标 \(i\)。增删的时候就把里面的 \(i\) 倒出来，找到它数论分块中的下一段，重新放到 \(q\) 中。然后因为 Note the unusual memory limit，需要对左右指针分别维护 \(ql,qr\)，每次用完一个立马 resize(3), shrink_to_fit()，或者可以使用你喜欢的 vector<int>().swap(V); 来释放内存。前者 push_back 的时候重新 resize() 有点麻烦。

Educational Codeforces Round 132 (Rated for Div. 2)

别骂了，本来是 noip 前过来找自信的，结果被虐到 remake。

C. Recover an RBS

存在性构造题。

果然，在看到问存在性的时候就应该意识到做法的。经典的括号序列，但问的是合法填写方案是否具有唯一性。如果问的是填写方案数，就是经典老题 CSP2021S 括号序列了，简洁做法可参见 这篇神仙题解。

但是这道题用不到 dp，只用括号序列的等价充要条件的性质——全局和为 0，且任意前缀和大于等于 0。因为是存在性问题，我们考虑构造最优方案，即极限情况，判断该方案的可行性及唯一性即可。具体地，左右括号的数量最终都是 \(\frac{n}{2}\)，所以问号中填的左右括号数量是确定的。贪心地，我们把左括号全部填左边，右括号全部填右边，这样能尽可能最大化任意前缀和。考虑求该方案的唯一性。显然，我们调换中间相邻那对左右括号的位置，满足调换后的方案是严格第二优的方案，此时直接判断该方案是否可行即可。

做法太神仙了。

E. XOR Tree

启发式合并。

前置结论：记 \(d_x\) 表示从 \(x\) 到根路径的异或和，那么路径 \((u,v)\) 的异或和为 \(d_u\ xor\ d_v\ xor\ a_{lca(u,v)}\)。

首先，因为题目没有限制更改后的数，所以可以随便改。以此为突破口，发现如果一个点更改成一个极大的 2 的次幂，那么经过它的所有路径都不可能为 0。考虑一个点在什么情况下会选择修改。最直观的原因是存在经过它的路径异或和为 0。考虑贪心。（说实话我不知道怎么自然地推到，直接上策略吧，可能需要头脑清醒才灵机一动推出来。）发现我们的贪心一定要和异或和为 0 的路径联系，不能直接按照深度或子树大小排。考虑对于一条异或和为 0 的路径，我们尽可能晚地去修改它。按深度从大到小遍历所有节点，如果在比它更深的节点都决定好是否修改之后，它的子树内还有异或和为 0 的路径，且路径的 lca 为它，说明它非改不可。
为什么一定要从深到浅？为什么一定要拖到 lca 才更改？假设当前路径为 (u,v)，存在另一条路径 (s,t) 满足和 (u,v) 有交且 lca(s,t) 比 lca(u,v) 浅，那么此时更改 lca(u,v) 一定能让 (s,t) 的异或和也不为 0。通过上述证明过程可知，若用调整法表述上述过程，即，考虑更改 (u,v) 上的点 x，使得 (u,v) 路径异或和不再为 0，且不存在比 (u,v) 深且与 (u,v) 有交的异或为 0 路径（否则 (u,v) 已经被影响到，成为合法的了），那么此时一定可以把 x 移到 lca(u,v) 满足结果一定不劣。

有了这个贪心之后，对于每个节点，只关心子树内当前是否存在异或和为 0 的、来自不同儿子的路径。用 map 维护是否需要更改当前节点，用 map 维护可达 \(O(n^2\log n)\)，用 unordered_map 维护可达 \(O(n^2)\)，外加喜闻乐见的 启发式合并 可达 \(O(n\log n)\)。

Codeforces Round 810 (Div. 2)

D. Rain

数形结合。

好题！这个递减加的之前洛谷某场比赛出过一道，那道正解拿二分做的，找了半天没找到题。话说这道题，如果有 \(x,p\leq 2e5\)，我想到了一个 \(O(n\log n)\) 的做法，算是弱化版解法吧：发现这个神奇的递减式加权值其实是在差分数组上给两段区间 区间加/减一。所以直接用线段树维护每个区间最大前缀和即可，判断是否有洪水直接判断 \(t_1.mx\) 和 \(m\) 的大小即可。

说回原题。我能说我做不出来是因为 mirror.codeforces.com 没有把样例解释的图给我放出来吗。根据样例解释，我们知道这道题用数形结合做很好做。发现，如果两个加区间叠加了，那么中间的重合的加区间的值是不变的，因为每往右移一位，一个少一，另一个加一，等于不变。如果把效果叠加在一起，体现为一个分段函数，每段都是一次函数，且斜率最多改变 \(O(n)\) 次。大概效果如下：

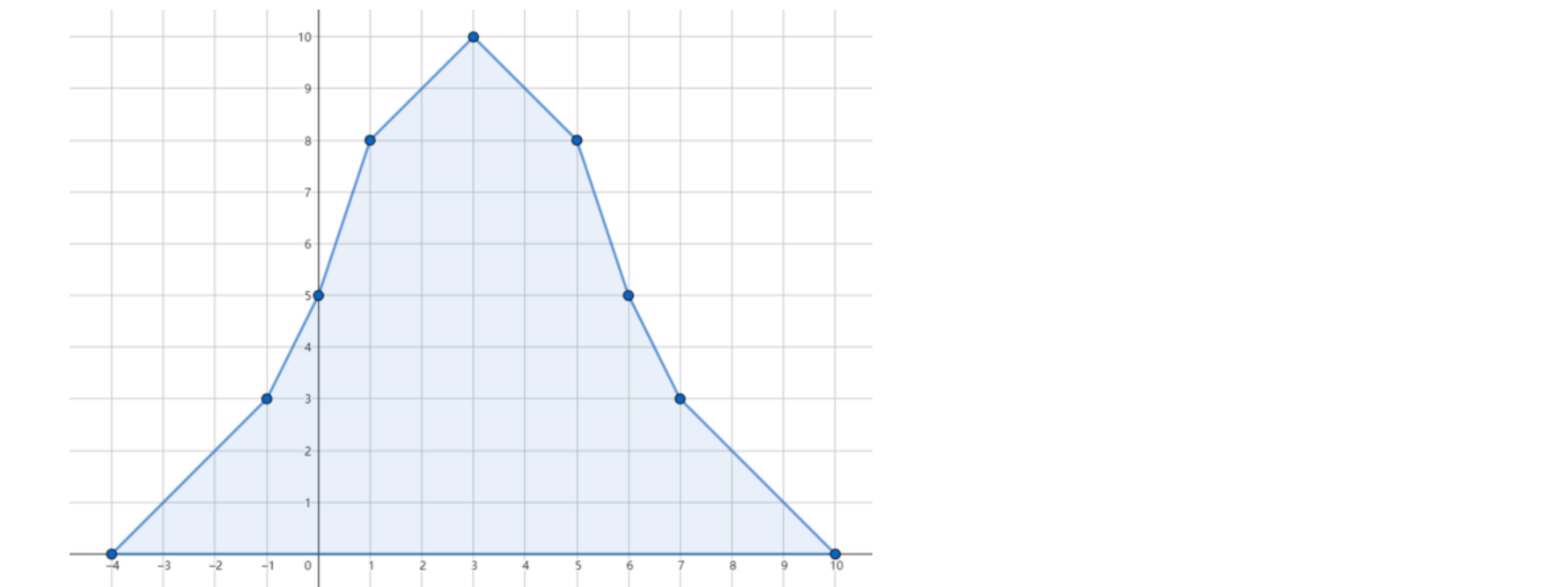
考虑求解问题。扒来 几个好图：
这个就是题目的问题，

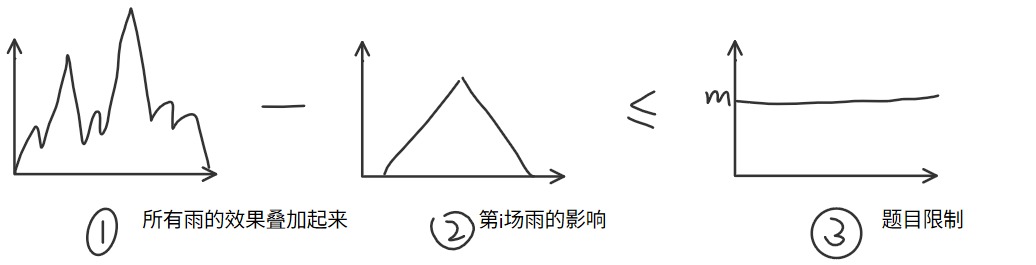
考虑转换验证方式，

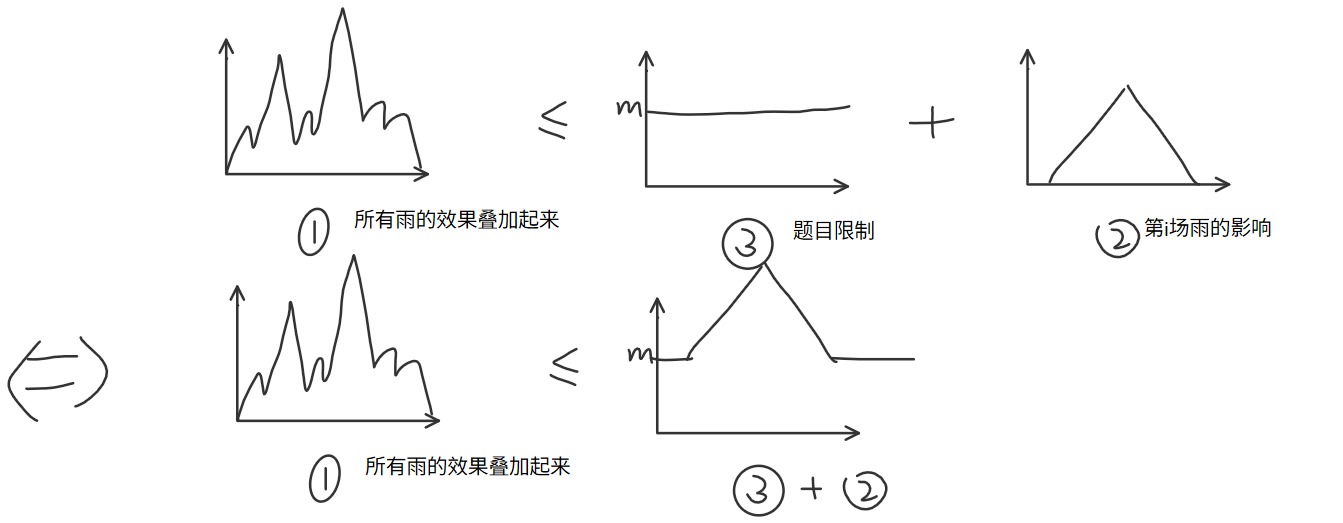
发现合法的情况就是所有的高峰都在红色部分之内，注意蓝色山顶的坐标为 \((x_i,p_i+m)\)。

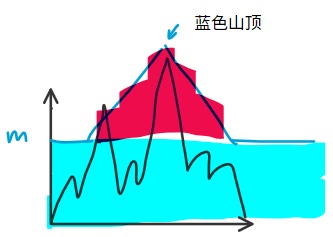
反过来，考虑每个高度 > m 的高峰，若它要被包含在红色部分，那么蓝色山顶必须落在它上方呈倒三角形的区域之中。最终蓝色山顶的合法区域就是所有红色部分的交。

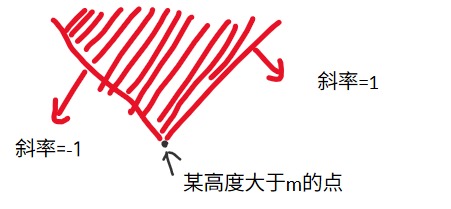
考虑如何求红色部分的交。发现倒三角的两边斜率绝对值都为 1，所以直接对截距取 max 即可。

实现的话直接维护二次差分数组即可。我们巧妙地使用 map 来巧妙地离散化，因为 map 内部有序且可以直接 for(auto it : mp) 直接有序访问内部的二元组。Code.

CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes!)

D. Magical Array

神仙构造题。

学到了，以后构造题想个二十分钟想不出来就不浪费时间了。看到题目第一反应肯定是去寻找所有序列操作后的共性，更具体地，找到剩下 n-1 个序列的共性。发现操作 1 中，下标一个左移一位，一个右移一位，增减的值相同，这启发我们寻找操作前后 \(\sum a_i\times i\) 的变化。然后你通过列式计算发现操作 1 前后这个值是没有变化的。同理，每做一次操作二，\(\sum a_i\times i\) 的值就会 +1。所以对于每个序列直接统计这个然后比较出现次数就能找到 k 了。