主席树(可持久化线段树)
前言
真不是有目的地学主席树的...(实在是因为它太上头了)
《关于我某天第二节晚修一直在看<进阶指南>可持久化数据结构这章然后学了主席树这件事》
update
- 2022-05-23:添加一些题型的整理。
主席树
也叫可持久化线段树、函数式线段树。其思想与可持久化 \(\mathtt{Trie}\) 相似。
其实,就是在普通线段树的基础上,修改了一下 \(\mathtt{update}\) 操作,使得它成为可持久化数据结构:
每次新建一个根节点,保存此次修改之后的状态。在遍历线段树的时候,对更改了的部分创建一个副本,然后直接将孩子指针指向上一个状态中没更改的部分。
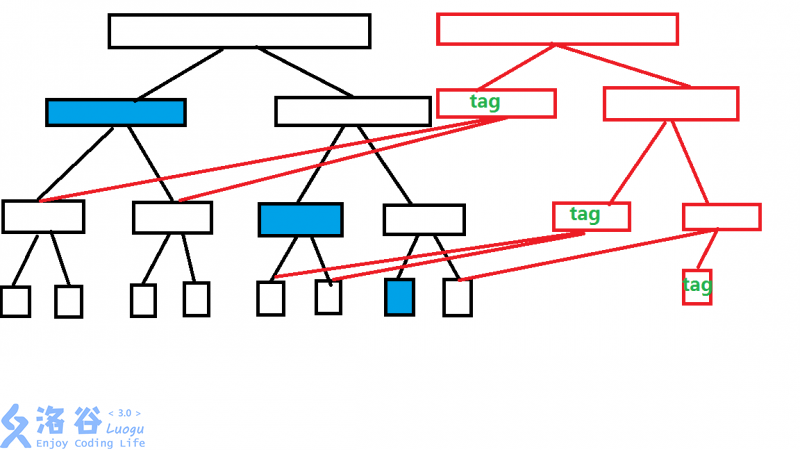
下面这张图展现了对 \([4,4]\) 修改后树的状态。

(注:图自此主席树博客)
不过主席树难以支持大部分的区间修改。原因是标记难以下传(后面有若干依赖此子树的树)。在一些特殊题目中,可以使用标记永久化代替标记的下传,例如:SP11470 TTM - To the moon。
对数组下标的划分
本质上就是用线段树实现可持久化数组。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
const int maxn = 1e6 + 5;
int n, m;
int a[maxn], rt[maxn];
struct node{
int l, r;
int val;
}t[maxn << 5];
int tot;
inline int build(int nw, int l, int r)
{
nw = ++tot;
if(l == r)
{
t[nw].val = a[l];
return nw;
}
int mid = (l + r) >> 1;
t[nw].l = build(t[nw].l, l, mid);
t[nw].r = build(t[nw].r, mid + 1, r);
return nw;
}
inline int cpy(int x)
{
int nw = ++tot;
t[nw] = t[x];
return nw;
}
inline int update(int lst, int l, int r, int k, int d)
{
int nw = cpy(lst), mid = (l + r) >> 1;
if(l == r)
t[nw].val = d;
else
{
if(k <= mid)
t[nw].l = update(t[nw].l, l, mid, k, d);
else t[nw].r = update(t[nw].r, mid + 1, r, k, d);
}
return nw;
}
inline int query(int nw, int l, int r, int k)
{
if(l == r)
return t[nw].val;
else
{
int mid = (l + r) >> 1;
if(k <= mid)
return query(t[nw].l, l, mid, k);
else return query(t[nw].r, mid + 1, r, k);
}
}
int main()
{
scanf("%d%d", &n, &m);
rep(i, 1, n) scanf("%d", &a[i]);
rt[0] = build(531, 1, n);
rep(i, 1, m)
{
int v, opt, loc, d;
scanf("%d%d%d", &v, &opt, &loc);
if(opt == 1)
{
scanf("%d", &d);
rt[i] = update(rt[v], 1, n, loc, d);
}
else
printf("%d\n", query(rt[v], 1, n, loc)),
rt[i] = rt[v];
}
return 0;
}
对值域的划分
离散化,然后对于每个根节点 \(root_i\),它维护的是数组从 \(a_1\) 到 \(a_i\) 中每个数的出现次数。
该算法时间复杂度为 \(O((N+M)logN)\),空间复杂度 \(O(NlogN)\)。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
const int maxn = 2e5 + 5;
int n, m;
struct node{
int ls, rs;
int sum;
}t[maxn << 5];
int a[maxn], b[maxn];
int q;
int dt, tot;
int rt[maxn];
inline void build(int &nw, int l, int r)
{
nw = ++tot;
if(l == r) return;
int mid = (l + r) >> 1;
build(t[nw].ls, l, mid), build(t[nw].rs, mid + 1, r);
}
inline int addt(int lst, int l, int r)
{
int nw = ++tot;
t[nw] = t[lst], t[nw].sum += 1;
if(l == r) return nw;
int mid = (l + r) >> 1;
if(dt <= mid) t[nw].ls = addt(t[nw].ls, l, mid);
else t[nw].rs = addt(t[nw].rs, mid + 1, r);
return nw;
}
inline int query(int pl, int pr, int l, int r, int k)
{
if(l == r) return l;
int mid = (l + r) >> 1, lcnt = t[t[pr].ls].sum - t[t[pl].ls].sum;
if(k <= lcnt)
return query(t[pl].ls, t[pr].ls, l, mid, k);
else return query(t[pl].rs, t[pr].rs, mid + 1, r, k - lcnt);
}
int main()
{
scanf("%d%d", &n, &m);
rep(i, 1, n)
scanf("%d", &a[i]), b[i] = a[i];
sort(b + 1, b + n + 1);
q = unique(b + 1, b + n + 1) - b - 1;
build(rt[0], 1, q);
rep(i, 1, n)
{
dt = lower_bound(b + 1, b + q + 1, a[i]) - b;
rt[i] = addt(rt[i - 1], 1, q);
}
rep(i, 1, m)
{
int lt, rtm, kt;
scanf("%d%d%d", <, &rtm, &kt);
int ans = query(rt[lt - 1], rt[rtm], 1, q, kt);
printf("%d\n", b[ans]);
}
return 0;
}
\(Emmm...\) 更有意思的是,这道题也可以使用线段树套平衡树的树套树做法,因为平衡树具有添加和删除的功能,所以这个做法支持动态修改。具体地...没写
关于对值域的划分,P4587 [FJOI2016]神秘数(题解)是道综合性较强的例题。
其他有趣的题型
1. 树状数组套主席树
此题先是运用了纯树状数组求逆序对的方法求出不带删去的逆序对个数(此方法《Tricks 整理》中有收录)。
其他细节见此篇题解。
每一次删除了一个数之后,我们要减去它和其它数组成的逆序对个数,加回和已经删除的数构成的逆序对的个数(前面统计过了)。
所以每次在加回的过程中,就变成在已删除的元素中,下表在 \([L,R]\) 中,大小在 \([l,r]\) 范围内的数的个数。
乍一看好像套一个值域上的主席树就可以了,但是在具体实现的过程中发现对于当前新添加的一个数,它的树根是 \(rt[p]\),但是它要在之前哪棵树的基础上建树呢?发现这是一个非常棘手的问题。
再加上我们要访问一个连续区间,单单用主席树去维护似乎变得不可行了。
所以此时我们要在主席树上套一个树状数组,用前缀和的思想去解决。
具体实现就是每次 \(update\) 时不仅仅在 \(rt[p]\) 上修改,还要在多个 \(rt[i]\) 上修改,查询就类似树状数组,区间和由前缀和相减得到。更多见代码。
但是!!这样我们会发现对于每一个 \(rt[i]\),都没有指向其他树以节省空间,只是能省空间则省空间(尽量少建节点),不过此题题目的空间限制也比一般题要大。
2. 按照 dfs 序建立主席树
对于每次询问,分两类情况讨论,要么 \(b\) 在 \(a\) 的子树内,要么 \(b\) 在 \(a\) 到根节点的路径上,两者都要满足 \(b\) 与 \(a\) 的距离小于等于 \(k\)。
后者显然容易处理,\(c\) 即为 \(a\) 子树中任意一点,这种情况的实现可直接间代码。
前者相对困难。发现 \(c\) 此时在 \(b\) 的子树内。所以这种情况的答案就是 \(\sum_b siz_b\)。而 \(siz_b\) 我们可以先 dfs 出来。
考虑如何求出合法的 \(b\)。我们要求的是:在 \(a\) 的子树中,与 \(a\) 这个节点的距离在 \([1,k]\) 的节点的 \(siz\) 之和。
依靠这个,我们可以建立一个主席树:
对于每一个节点,有 \(far_i\) 表示它到根节点 1 的距离。那么此时,“与 \(a\) 这个节点的距离在 \([1,k]\)”这个限制就变为 \(far[i] \in [far_a+1,far_a+k]\)。
那“a 的子树”这个限制如何转化?打破定式思维,我们在 dfs 的过程中给每个点一个 dfs 序,然后按照这个 dfs 序去建树,所以,此时我们询问的范围就变成了 \([rt[id_a],rt[id_a+siz_a-1]]\)。
此时也不难想到对于主席树内的节点的权值就设为其对应点的 \(siz\) 值了。
3. 主席树在值域上维护求中位数
这个相对于前两种就简单多了,不过此题的重点在与求解不定区间的中位数。
在主席树这方面特别要注意的是,对于一棵根为 \(rt_i\) 的树,我们对它的两个子树都各要有一个标记,记录着这个子树是不是一个新建的节点。如果它不是一个新建的节点(即直接指向前面的树的对应子树),后续要在这棵树上修改时,就不能直接修改,影响前面的子树,而要新建节点再修改。
需要这个标记的前提是主席树内的一棵树 \(rt[i]\),它的子树可能会被多次修改。
其他细节见【LG-P2839 [国家集训队]】middle 题解
4. 可持久化并查集
辛酸血泪史, 说白了就是 可持久化数组 + 并查集。
注意此处的并查集不需要路径压缩,因为主席上进行更改的复杂度是 \(O(logn)\) 的。
此外还要注意的就是对于一个节点 \(i\),既要对其父亲单独建立一棵树,也要对其深度单独建立一棵树。
具体见代码。
5. 标记永久化
回过头去做标记永久化,发现比想象中要简单。
标记永久化,顾名思义,标记不需要下传,主要用于主席树上的区间修改。
对被修改区间覆盖的节点打上标记,其左右子节点继承上个版本的左右子节点。
(图自此博客)
这样可以保证修改不影响公共节点了。具体看代码。
这里放一些重点:
- 区间修改:
inline void update(int &x, int lst, int l, int r, int L, int R, int d){
if(!x) x = ++tot;
t[x] = t[lst], t[x].sum += d * (min(R, r) - max(l, L) + 1);
if(l >= L and r <= R){
t[x].tag += d;
return;
}
int mid = l + r >> 1;
if(L <= mid) ls = 0, update(ls, t[lst].l, l, mid, L, R, d);
if(R > mid) rs = 0, update(rs, t[lst].r, mid + 1, r, L, R, d);
}
- 区间查询:
inline int query(int x, int ln, int rn, int L, int R){
if(ln >= L and rn <= R)
return t[x].sum;
int mid = ln + rn >> 1, s = 0;
if(L <= mid) s += query(ls, ln, mid, L, R);
if(R > mid) s += query(rs, mid + 1, rn, L, R);
return s + t[x].tag * (min(R, rn) - max(ln, L) + 1);
}
——\(\mathfrak{End}\)——




 浙公网安备 33010602011771号
浙公网安备 33010602011771号