[来源不详]gentree 奇技淫巧法with图论

Description

给你一个有向连通图G，每点有个权值D_i（0<D_i），要求生成一棵树根为1号节点的有根树T。对于树中边E，E的代价为所有从根出发的且包含E的路径的终点权值的和。现求生成树T，使得边的代价总和最小。

Input

第一行N,M分别为点数，边数。（0<=N <= 20000；0<=M <= 200000）

接下来M行，每行两个数U，V描述边的两个端点，即从U到V有一条有向边。

最后一行N个数，顺次给出每个点的权值。

Output

一个数，最小代价。

Sample Input

5 4

1 2

1 3

3 4

3 5

1 2 3 4 5

Sample Output

23

Hint

样例解释：

如图只有一种生成树的方法，求得代价为23。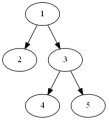

数据规模：

所有数据保证不会超过长整型（C++中的int）。

---

一开始做这道题的时候呢，我完美地理解错了题意，我tm以为每个节点的位置是固定的，所以我直接dfs一遍把所有的边权都求了出来，然后做最小生成树（好傻逼的做法）。

这是错的代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define ll long long
#define il inline
#define db double
using namespace std;
il int gi()
{
    int x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
il ll gl()
{
    ll x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
int head[200045],cnt;
struct edge
{
    int lon,next,to,from;
}e[200045];
il void add(int from,int to)
{
    e[++cnt].to=to;
    e[cnt].from=from;
    e[cnt].next=head[from];
    head[from]=cnt;
}
int point[20045];
int dfs(int x)
{
    int r=head[x],sum=0;
    while(r!=-1)
    {
        e[r].lon+=dfs(e[r].to)+point[e[r].to];
        sum+=point[e[r].to];
        r=e[r].next;
    }
    return sum;
}
bool cmp(edge a,edge b)
{
    return a.lon<b.lon;
}
int fa[20045];
int find(int x)
{
    if(fa[x]!=x)
    fa[x]=find(fa[x]);
    return fa[x];
}
int main()
{
    freopen("gentree.in","r",stdin);
    freopen("gentree.out","w",stdout);
    memset(head,-1,sizeof(head));
    int n=gi(),m=gi(),x,y;
    for(int i=1;i<=n;i++)
    fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        x=gi(),y=gi();
        add(x,y);
    }
    for(int i=1;i<=n;i++)
    point[i]=gi();
    dfs(1);
    sort(e+1,e+1+cnt,cmp);
    int num=0,ans=0;
    for(int i=1;i<=cnt;i++)
    {
        if(num>n)
        break;
        int r1=find(e[i].from),r2=find(e[i].to);
        if(r1!=r2)
        {
            num++;
            fa[r2]=r1;
            ans+=e[i].lon;
        }
    }
    printf("%d\n",ans);
    return 0;
}

后来，看了题解后， 光 然大悟。

首先，我们其实可以简化一下题目。

我们知道每条边的边权都是它的子树的点的权值和，那么我们就可以把边权和看成所有点的点权*该点对应的深度。

这样一来就好做了许多。

所以我们以1为起点跑一遍最短路，然后把每个点到1的距离乘以点权就是答案。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define ll long long
#define il inline
#define db double
using namespace std;
il int gi()
{
    int x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
il ll gl()
{
    ll x=0,y=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
        y=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*y;
}
int head[200045],cnt;
struct edge
{
    int to,next;
}e[200045];
il void add(int from,int to)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    head[from]=cnt;
}
int t[20045];
int headd,tail=1;
int dist[20045];
bool vis[20045];
il void spfa()
{
    printf("wdadw");
    t[0]=1;
    dist[1]=0;
    vis[1]=1;
    while(headd!=tail)
    {
        printf("headd=%d tail=%d\n",headd,tail);
        int r=head[t[headd]];
        while(r!=-1)
        {
            if(dist[e[r].to]>1+dist[t[headd]])
            {
                dist[e[r].to]=1+dist[t[headd]];
                if(!vis[e[r].to])
                {
                    vis[e[r].to]=1;
                    t[tail++]=e[r].to;
                }
            }
            r=e[r].next;
        }
        vis[t[headd]]=0; 
        headd++;
    }
}
int point[200045];
int main()
{
    freopen("gentree.in","r",stdin);
    freopen("gentree.out","w",stdout);
    memset(head,-1,sizeof(head));
    memset(dist,127/3,sizeof(dist));
    int n=gi(),m=gi(),x,y;
    for(int i=1;i<=m;i++)
    {
        x=gi(),y=gi();
        add(x,y);
    }
    for(int i=1;i<=n;i++)
    point[i]=gi();
    spfa();
    int ans=0;
    for(int i=1;i<=n;i++)
    ans+=point[i]*dist[i];
    printf("%d\n",ans);
    return 0;
}