最大正方形问题

最大正方形问题

作者：Grey

原文地址：

博客园：最大正方形问题

CSDN：最大正方形问题

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

题目链接见：LeetCode 221. Maximal Square

主要思路

本题思路比较简单，可以定义一个二维数组dp，二维数组dp的规模和原始矩阵的规模一样。

int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m][n];

其中dp[i][j]表示正方形必须以 i, j 作为右下角的情况下，哪个正方形内部都是 1 且最大。

有一个很显而易见的结论，如果matrix[i][j] == '0'，则dp[i][j] = 0，接下来是 base case，

第一行和第一列的值很容易可以得到

  for (int i = 0; i < m; i++) {
    dp[i][0] = matrix[i][0] == '1' ? 1 : 0;
    max = Math.max(dp[i][0], max);
}
for (int i = 0; i < n; i++) {
    dp[0][i] = matrix[0][i] == '1' ? 1 : 0;
     max = Math.max(dp[0][i], max);
}

注：max变量用于记录全局最大值。

考虑普遍位置，如下图

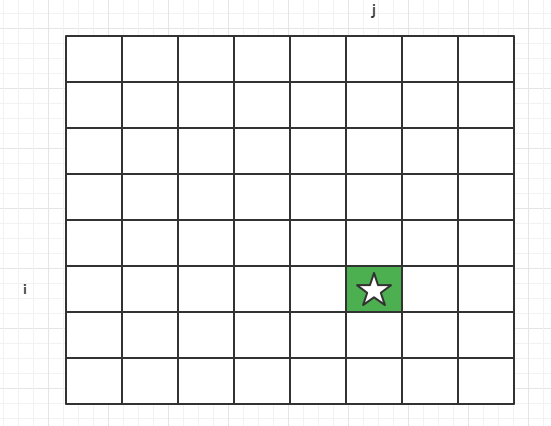
观察dp[i][j]周围的位置依赖，有如下两种情况

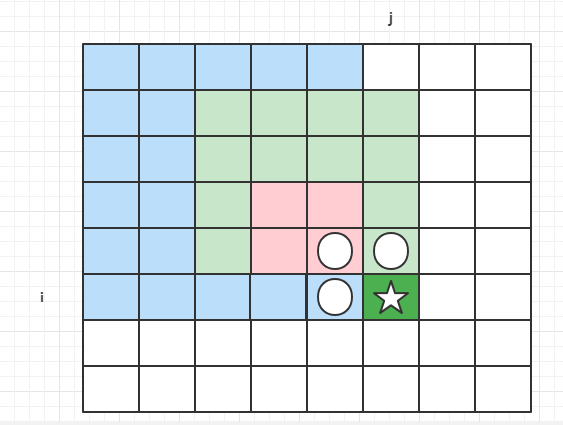
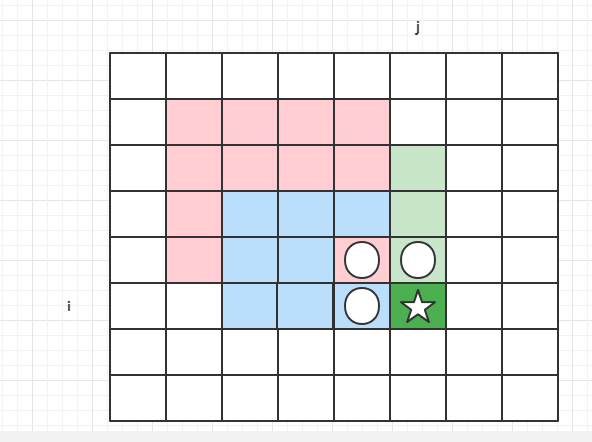
其中dp[i-1][j]表示的区域是绿色部分的正方形，dp[i-1][j-1]表示的区域是红色部分的正方形，dp[i][j-1]表示蓝色区域部分的正方形，基于上述上个位置的值，可以得到dp[i][j]的值，即dp[i][j]依赖其左边一个位置，上面一个位置，左上角位置。

代码如下

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = matrix[i][j] == '1' ? Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1 : 0;
                max = Math.max(dp[i][j], max);
            }
        }

完整代码见

class Solution {
    public int maximalSquare(char[][] matrix) {
        if (null == matrix || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int max = 0;
        // tips 正方形必须以i,j作为右下角情况，哪个正方形内部都是1且最大
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = matrix[i][0] == '1' ? 1 : 0;
            max = Math.max(dp[i][0], max);
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = matrix[0][i] == '1' ? 1 : 0;
            max = Math.max(dp[0][i], max);
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = matrix[i][j] == '1' ? Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1 : 0;
                max = Math.max(dp[i][j], max);
            }
        }
        return max * max;
    }
}

更多

算法和数据结构笔记