前缀树的设计与实现

前缀树的设计与实现

作者：Grey

原文地址：

博客园：前缀树的设计与实现

CSDN：前缀树的设计与实现

前缀树即字典树，可以利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较。

我们使用搜索引擎的时候，输入 test，后面会自动显示一堆前缀是 test 的东西。这就利用了前缀树结构来实现。

比如我们有一堆字符串

["Trie","apple", "insert","apple", "search", "app","search", "startsWith", "insert", "search"]

问题1.查询字符串列表里面是否有以app，apx为前缀的字符串。

问题2.查询字符串列表里面有没有insert和serac这两个字符串。

我们可以把字符串列表构造成一棵前缀树，如下图

头节点是空串，路径表示字符，节点表示一个字符串的前缀（简称 p 节点），黑色节点表示一个字符串的结尾位置（简称 e 节点）。

有了如上结构，针对问题1，判断是否存在app前缀的字符串，流程如下

头节点开始，先看有没有走向a的路径，有，则移动指针往a的路径走，
然后判断是否有走向p的路径，有，则移动指针往p的路径走，
然后判断是否有走向p的路径，有，则移动指针往p的路径走，

则存在以app为前缀的字符串。

同理，回到头节点，继续判断apx，发现到没有到x的路径，则直接返回不存在以apx为前缀的字符串。

针对问题2，判断是否有insert这个字符串，流程和判断前缀的流程一样，只不过到了末尾位置，判断是否是黑色节点，如果是黑色节点，说明存在这样的字符串，否则不存在。

更进一步，前缀树也可以支持加入元素和删除元素，此时，我们需要在 p 节点和 e 节点记录一个出现次数的信息，如上例，记录次数后，前缀树如下图

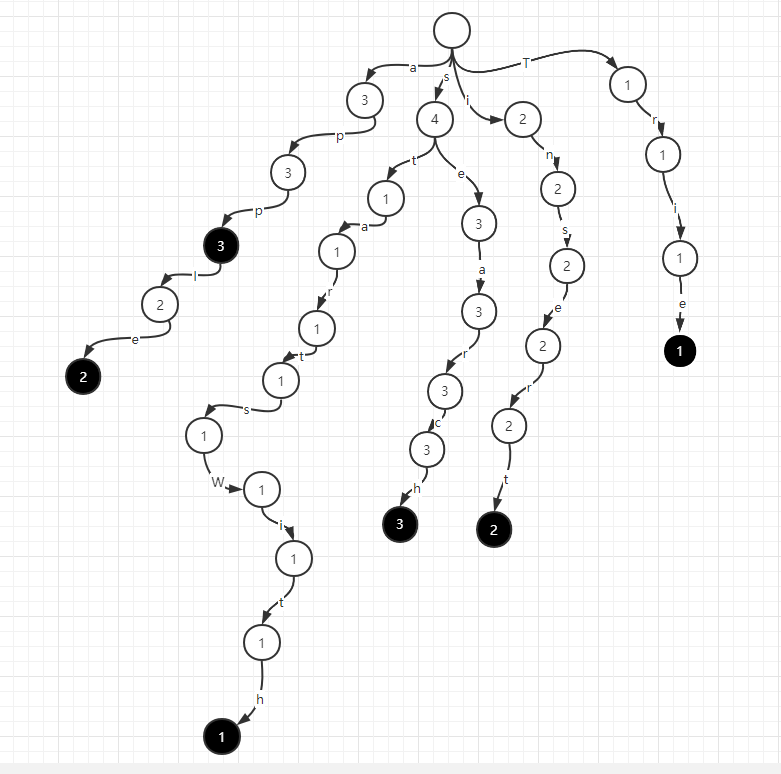
如果要删除一个apple字符串，前缀树在apple的路径上依次减一即可

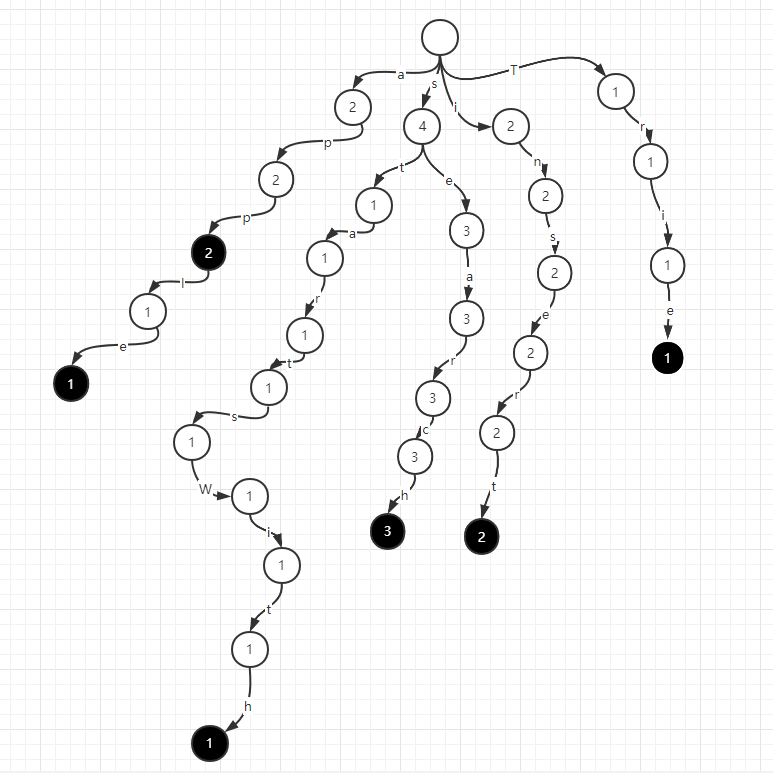
如果要继续增加一个apx字符串，前缀树继续建出apx的路径即可。

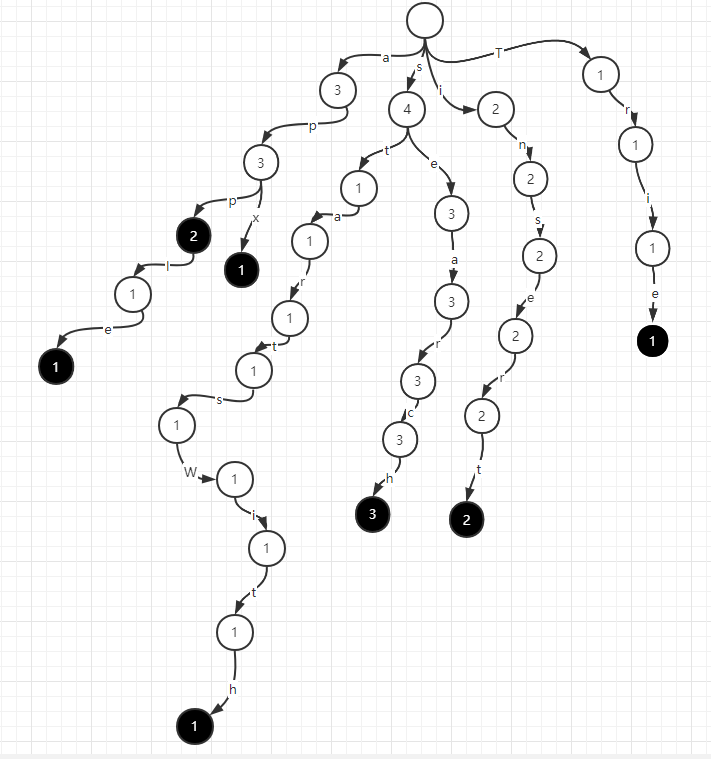
依据上述流程，我们可以用 Hash 表实现前缀树，代码如下

import java.util.HashMap;

public static class Node2 {
    public int pass;
    public int end;
    public HashMap<Integer, Node2> nexts;

    public Node2() {
        pass = 0;
        end = 0;
        nexts = new HashMap<>();
    }
}

public static class Trie2 {
    private final Node2 root;

    public Trie2() {
        root = new Node2();
    }

    public void insert(String word) {
        if (word == null || word.isEmpty()) {
            return;
        }
        char[] str = word.toCharArray();
        Node2 cur = root;
        cur.pass++;
        int n = 0;
        for (char v : str) {
            n = v;
            if (!cur.nexts.containsKey(n)) {
                cur.nexts.put(n, new Node2());
            }
            cur.nexts.get(n).pass++;
            cur = cur.nexts.get(n);
        }
        cur.end++;
    }

    public void delete(String word) {
        if (search(word) == 0) {
            return;
        }
        char[] str = word.toCharArray();
        Node2 cur = root;
        cur.pass--;
        for (char v : str) {
            int n = v;
            if (--cur.nexts.get(n).pass == 0) {
                cur.nexts.remove(n);
                return;
            }
            cur = cur.nexts.get(n);
        }
        cur.end--;
    }

    // word这个单词之前加入过几次
    public int search(String word) {
        if (word == null || word.isEmpty()) {
            return 0;
        }
        char[] str = word.toCharArray();
        Node2 cur = root;
        for (char v : str) {
            if (!cur.nexts.containsKey((int) v)) {
                return 0;
            }
            cur = cur.nexts.get((int) v);
        }
        return cur.end;
    }

    // 所有加入的字符串中，有几个是以pre这个字符串作为前缀的
    public int prefixNumber(String pre) {
        if (pre == null || pre.isEmpty()) {
            return 0;
        }
        char[] str = pre.toCharArray();
        Node2 cur = root;
        for (char v : str) {
            if (!cur.nexts.containsKey((int) v)) {
                return 0;
            }
            cur = cur.nexts.get((int) v);
        }
        return cur.pass;
    }
}

如果字符串只由 26 个英文字母组成，那么可以用一个包含 26 个字符的数组来替代上述前缀树中的哈希表，Node节点的数据结构可以优化成

class Node {
    int p;
    int e;
    Node[] nodes = new Node[26];
}

判断流程调整为：

nodes[0] != null：表示有走向a的路，否则则没有走向a的路;

nodes[1] != null：表示有走向b的路，否则则没有走向b的路;

nodes[2] != null：表示有走向c的路，否则则没有走向c的路;

...

nodes[25] != null：表示有走向z的路，否则则没有走向z的路;

LeetCode 有对应的题目链接：见：LeetCode 208. Implement Trie (Prefix Tree)

完整代码如下

class Trie {
    class Node {
        int p;
        int e;
        Node[] nodes = new Node[26];
    }

    Node root;

    public Trie() {
        root = new Node();
    }

    public void insert(String word) {
        char[] str = word.toCharArray();
        Node cur = root;
        for (char c : str) {
            cur.p++;
            if (cur.nodes[c - 'a'] == null) {
                cur.nodes[c - 'a'] = new Node();
            }
            cur = cur.nodes[c - 'a'];
        }
        cur.e++;
    }

    public boolean search(String word) {
        char[] str = word.toCharArray();
        Node cur = root;
        for (char c : str) {
            if (cur.nodes[c - 'a'] == null) {
                return false;
            }
            cur = cur.nodes[c - 'a'];
        }
        return cur.e != 0;
    }

    public boolean startsWith(String prefix) {
        char[] str = prefix.toCharArray();
        Node cur = root;
        for (char c : str) {
            if (cur.nodes[c - 'a'] == null) {
                return false;
            }
            cur = cur.nodes[c - 'a'];
        }
        return true;
    }
}

本文的所有图例见: processon:前缀树的设计和实现

更多

算法和数据结构学习笔记

算法和数据结构学习代码