跳表的设计和实现
跳表的设计和实现
作者:Grey
原文地址:
说明
数组的查询速度很快O(1), 但是插入的速度比较慢O(N), 链表的插入速度快O(1), 但是链表的查询速度比较慢O(N)。 而跳表的平均查找和插入时间复杂度都是O(logN),空间复杂度O(N)
流程
题目中规定了节点值的数据范围
[0,20000]
假设要加入的数据依次是:
[5, 43, 6, 1, 3, 8, 5]
现在要把这些数据组织成跳表
首先,设计跳表节点的数据结构,为了便于跳表节点可以上下左右寻找到对应节点,我们设计跳表节点的结构如下:
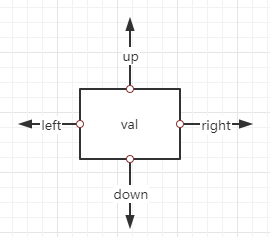
首先,我们需要先准备一个头节点,这个头节点是整个跳表的最小值,可以根据节点值的范围来确定,因为节点值都大于等于0,所以,头节点的值我准备一个-1即可。

准备好头节点以后,我们开始放入第一个元素:5
放入元素之前,我们需要做两件事:
第一件事: 找到目前小于等于5的最大的元素,假设是a,把5这个元素连到a的后面,如果a的下一个元素是c,那么连好后应该是
a -> 5 -> c
第二件事: 通过掷色子的方式(简单理解成随机生成一个整数值),随机给5这个元素增加层数,并逐层连好。
上述两点说的比较抽象,如果用图示来表达的话,在现在跳表只有-1这个节点的情况下,
经历了第一件事之后,跳表结构应该是这样的:

经历了第二件事以后(假设生成的随机层数是3),跳表的结构会变成:
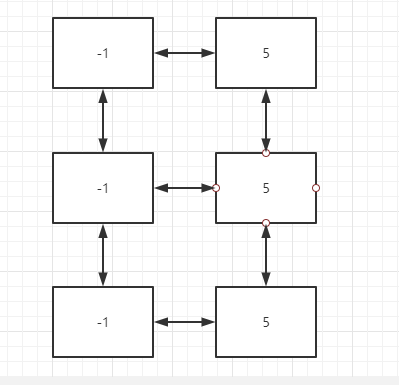
此时,第一个元素5,就安排好了,接下来安排第二个元素:43,假设43生成的随机层数是:2,那么做完上述两件事后,跳表的样子会变成如下:

注:此时,跳表的最高层数是3,我们有一个规定:头节点链表的长度一定和最大层数要保持一致
接下来处理6这个元素,假设6对应获取到的层数是:4
4已经超过了目前的最大层数3,所以,要扩充头节点链表,且6必须插在5和43之间,所以,6这个元素加入到跳表后,跳表的样子如下:
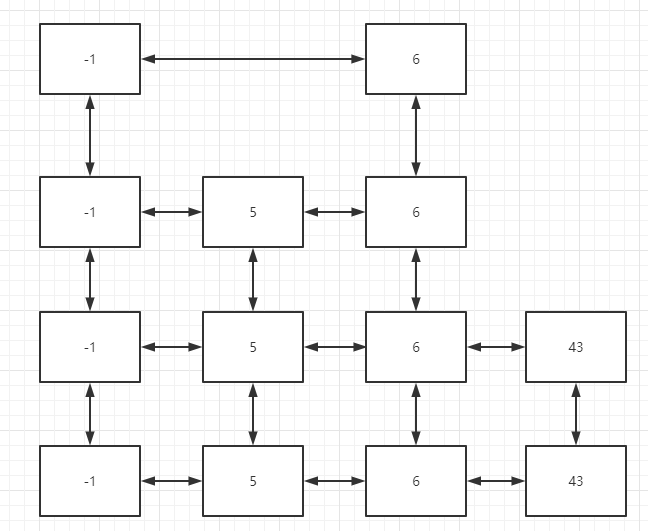
同理,假设1,3,8对应的层数分别是2,4,1,那么经历过上述处理后,跳表变成了这个样子:
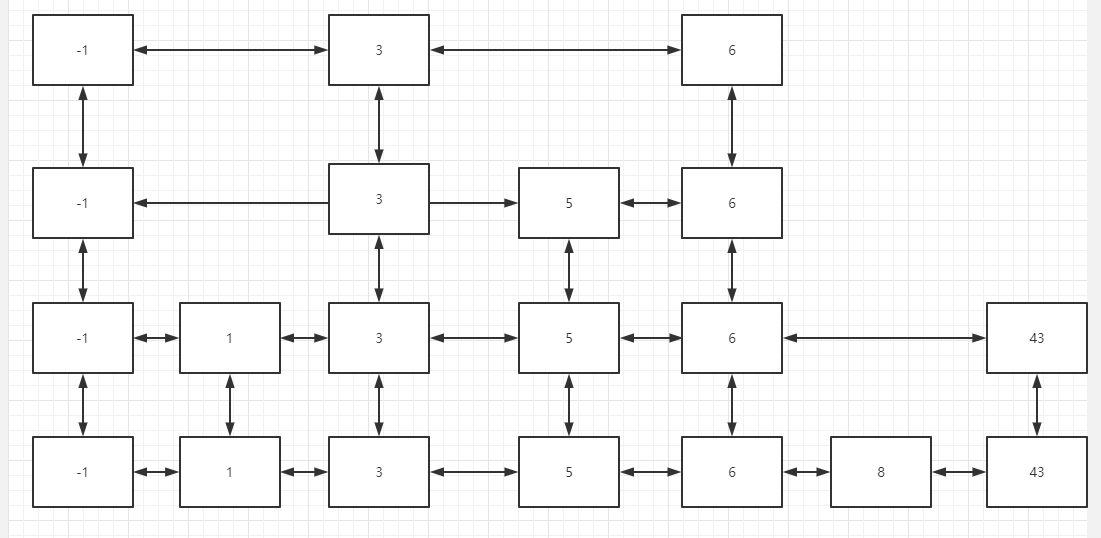
最后一个元素5,假设对应的层数是1,因为题目说需要支持重复值,那么把这个5放到原有跳表的下一个位置即可(如下图中绿色的点),最后生成的跳表格式为:

如图可知,最底层有所有的元素值,每次查询的时候,是从头节点的最高层开始,比如,我们要查询8这个元素,那么整个跳表会历经如下蓝色的点:
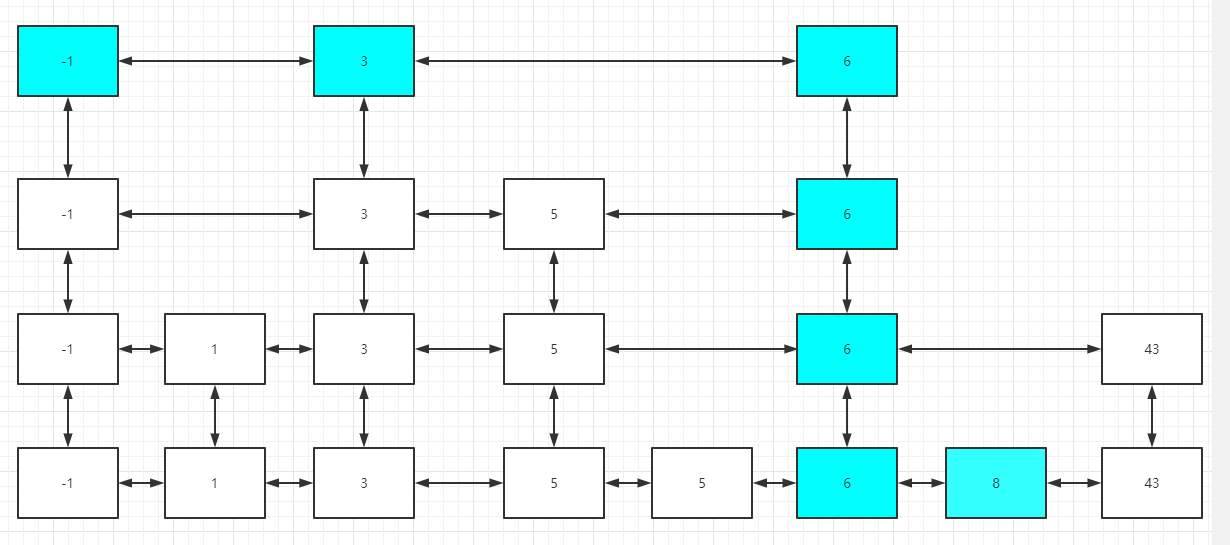
这样的查询,每次高层走一步,其实底层会直接过滤掉一批节点,提高了查询的效率。
如果要删除一个节点,其实我们只需要在还有这个节点的每一层做单链表的删除元素操作即可,比如,我们需要删除a这个元素,我们需要做两件事:
-
找到a这个节点最底层的位置,如果找不到,直接不需要操作删除。
-
找到a这个节点在的底层位置,依次往上(node = node.up),删掉每一个元素,直到不能往上为止。
假设,我们要删除3这个元素。
我们首先找到了3这个元素,所在的最底层位置,如下图:
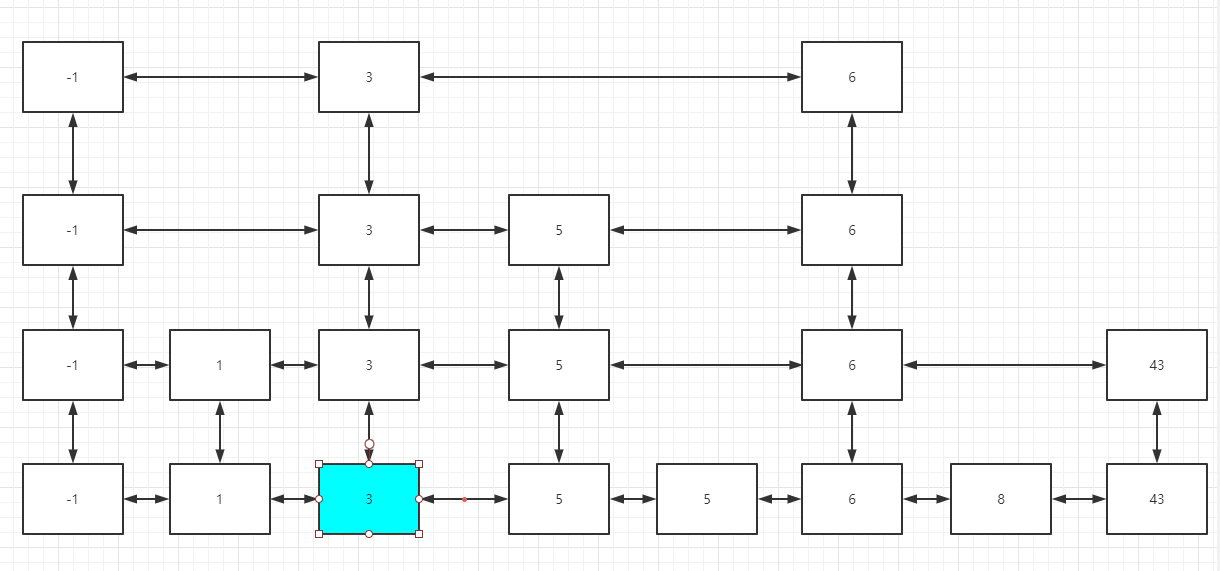
然后删掉这个元素,并来到3所在的第二层位置:
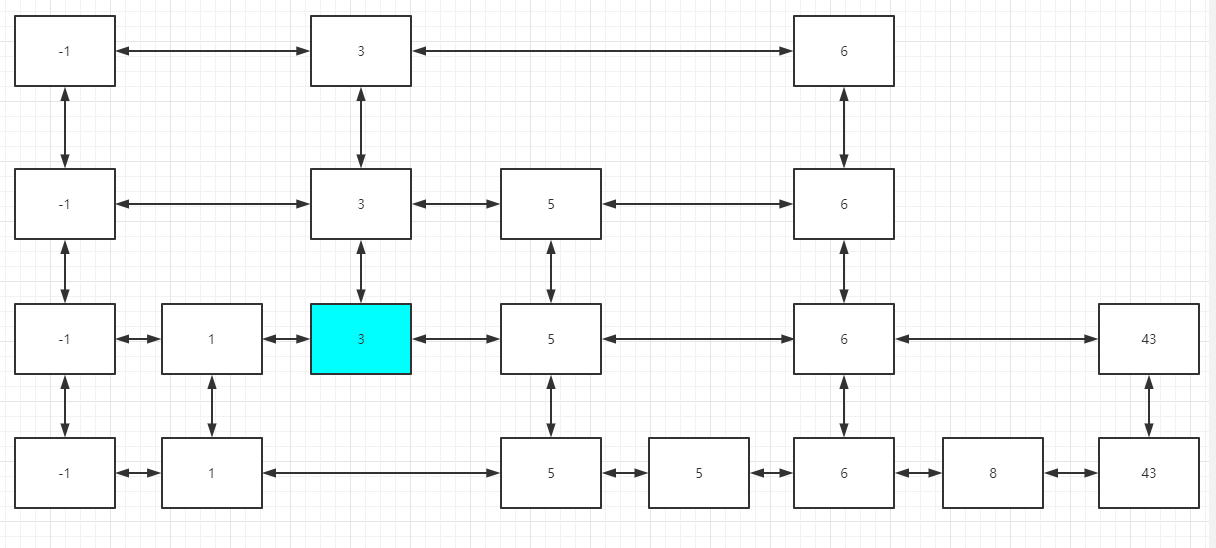
继续删除
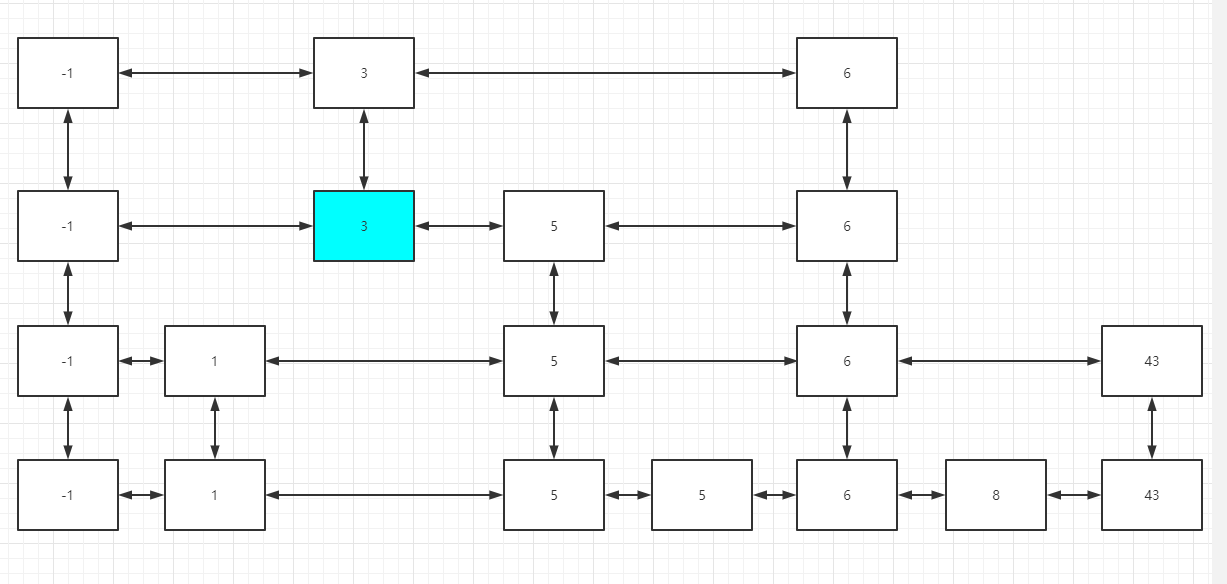
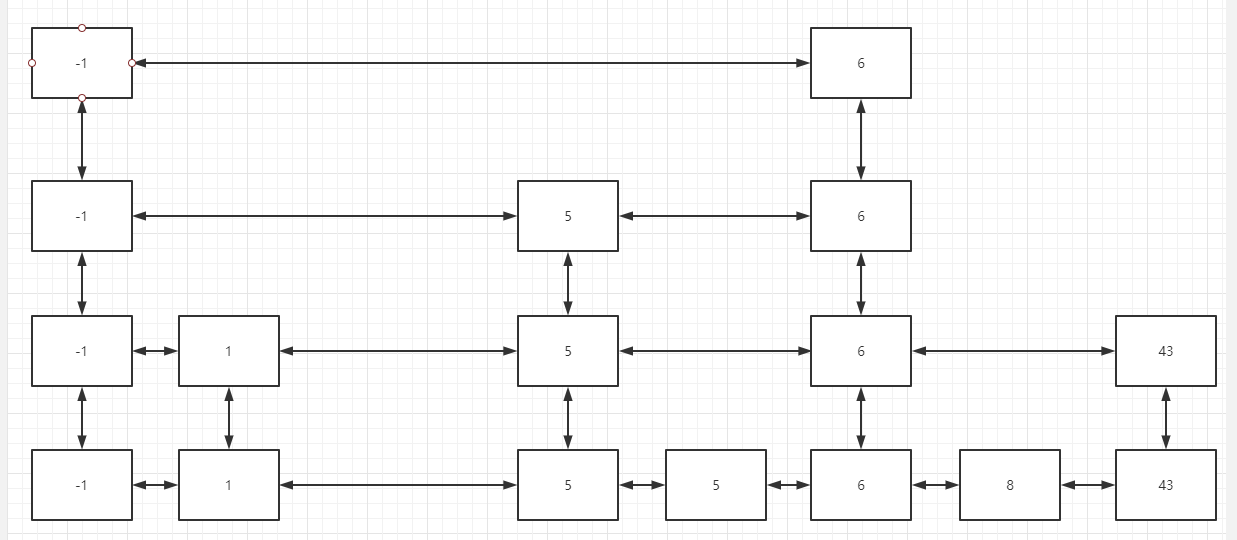
最后,删除所有的3以后,跳表如下:
细节
通过如上流程,我们需要实现跳表的初始化,增加元素,删除元素,至少需要实现如下的一些方法:
随机生成层数
如下代码
// < 0.5 : 增加一层,
// >= 0.5 :不再增加
public boolean roll() {
return Math.random() < 0.5d;
}
获取跳表中小于或某个元素的最右位置的元素
public Node getLessOrEqual(int target) {
// 获取头节点的最顶端的位置的那个元素
Node cur = heads.get(heads.size() - 1);
while (cur != null) {
// 如果比目标值小,就一直向右边移动(在右边不为空的情况下),如果右边为空了,继续向下移动,直到移动到最底端。
if (cur.right == null || cur.right.val > target) {
if (cur.val <= target) {
if (cur.down != null) {
cur = cur.down;
} else {
break;
}
}
} else {
cur = cur.right;
}
}
return cur;
}
有了这两个功能函数,其他的实现,就是利用这两个函数做一些双向链表的节点操作,只不过这个双向链表的节点还保存了其上一层位置的节点指针和下一层位置的节点指针。
完整代码
class Skiplist {
private final ArrayList<Node> heads;
private final static double POSSIBLE = 0.5d;
public Skiplist() {
heads = new ArrayList<>();
heads.add(new Node(-1));
}
public static class Node {
private int val;
private Node up, down, left, right;
public Node(int val) {
this.val = val;
}
}
public Node getLessOrEqual(int target) {
Node cur = heads.get(heads.size() - 1);
while (cur != null) {
if (cur.right == null || cur.right.val > target) {
if (cur.val <= target) {
if (cur.down != null) {
cur = cur.down;
} else {
break;
}
}
} else {
cur = cur.right;
}
}
return cur;
}
public boolean search(int target) {
return getLessOrEqual(target).val == target;
}
public boolean roll() {
return Math.random() < POSSIBLE;
}
public void add(int num) {
// 如果节点存在则不增加
Node lessOrEqual = getLessOrEqual(num);
// 支持重复数据插入,所以这里不能直接判断存在就退出
/* if (lessOrEqual.val == num) {
return;
}*/
// 到这里说明节点不存在,先建出节点
Node newNode = new Node(num);
// 无论如何,最底层都要连起来的
Node right = lessOrEqual.right;
lessOrEqual.right = newNode;
newNode.left = lessOrEqual;
if (right != null) {
// lessOrEqual不是最后一个节点
newNode.right = right;
right.left = newNode;
}
// 掷骰子随机确定其他的层数
Node pre = lessOrEqual;
Node cur = newNode;
while (roll()) {
while (pre.left != null && pre.up == null) {
pre = pre.left;
}
if (pre.left == null) {
// 到达heads节点
final Node head = new Node(-1);
pre.up = head;
head.down = pre;
heads.add(head);
}
pre = pre.up;
Node toInsert = new Node(num);
cur.up = toInsert;
toInsert.down = cur;
cur = cur.up;
pre.right = toInsert;
cur.left = pre;
}
}
public boolean erase(int num) {
Node lessOrEqual = getLessOrEqual(num);
if (lessOrEqual.val != num) {
return false;
}
Node cur = lessOrEqual;
while (cur != null) {
Node pre = cur.left;
Node after = cur.right;
pre.right = after;
if (after != null) {
after.left = pre;
}
cur = cur.up;
}
return true;
}
}
跳表的应用
Redis底层使用了跳表,为什么选跳表而不是AVL树或者SBT红黑树来实现,因为跳表方便序列化。
更多
参考资料
本文来自博客园,作者:Grey Zeng,转载请注明原文链接:https://www.cnblogs.com/greyzeng/p/14429103.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号