力扣 leetcode 1091. 二进制矩阵中的最短路径

问题描述

给你一个 n * n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

• 路径途经的所有单元格都的值都是 0 。
• 路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
• 畅通路径的长度 是该路径途经的单元格总数。

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 为 0 或 1

示例

示例 1：

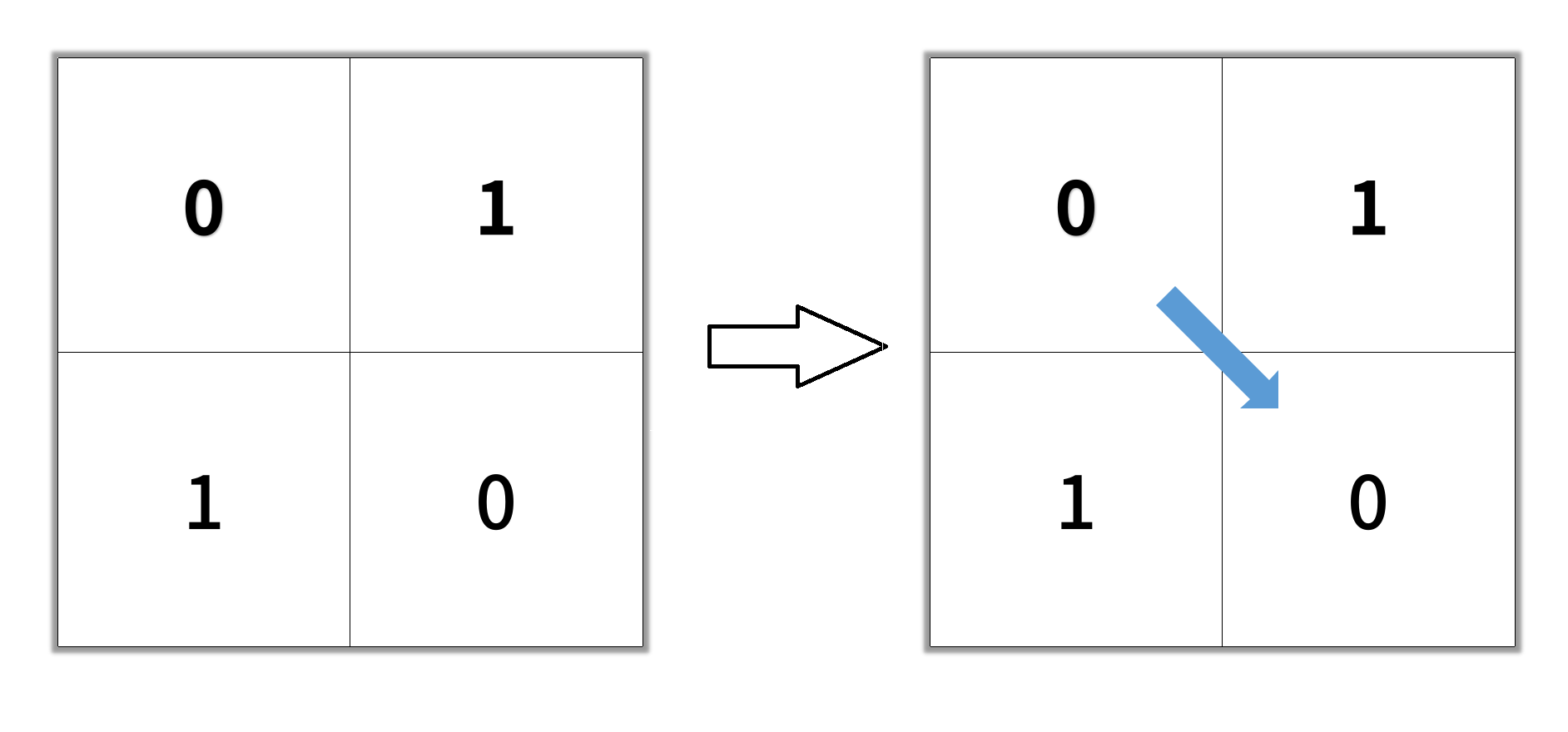
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

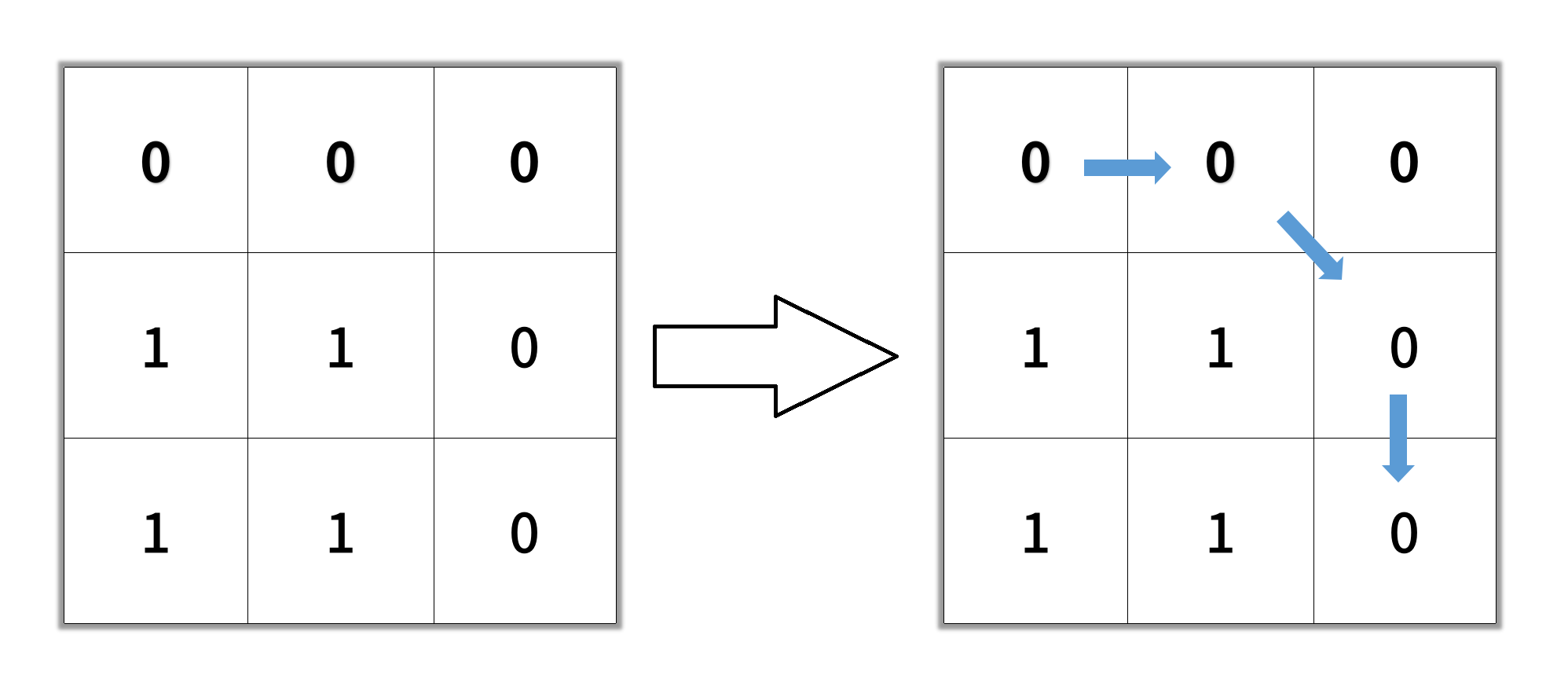
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

解题思路

本题实际上要求从一个点到另一个点的最短路径，我们可以用 BFS 来搜索，判断是否存在一条路径，以及计算路径的最短距离。这里如果使用 DFS 来求解的话，很容易超时，因为 DFS 更新距离时，可能会要更新之前遍历过的节点，为了保证结果的可靠性，又要重新遍历一次，这导致了很多重复的计算开销。而 BFS 中不存在这样的问题。

class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        const int n = grid.size();
        if(grid[0][0] || grid[ n - 1][n - 1]){
            return -1;
        }
        if(n < 3){
            return n;
        }
        vector<vector<int>> steps(n, vector<int>(n, -1));
        queue<pair<int, int>> s;
        s.emplace(0, 0);
        steps[0][0] = 1;
        pair<int, int> tmp;
        int x, y;
        while(!s.empty()){
            tmp = s.front();
            x = tmp.first;
            y = tmp.second;
            s.pop();
            if(x > 0){
                if(y > 0){
                    if(!grid[x - 1][y - 1] && steps[x - 1][y - 1] < 0){
                        s.emplace(x - 1, y - 1);
                        steps[x - 1][y - 1] = steps[x][y] + 1;
                    }
                }
                if(!grid[x - 1][y] && steps[x - 1][y] < 0){
                    s.emplace(x - 1, y);
                    steps[x - 1][y] = steps[x][y] + 1;
                }
                if(y < (n - 1)){
                    if(!grid[x - 1][y + 1] && steps[x - 1][y + 1] < 0){
                        s.emplace(x - 1, y + 1);
                        steps[x - 1][y + 1] = steps[x][y] + 1;
                    }
                }
            }
            if(y > 0 && !grid[x][y - 1] && steps[x][y - 1] < 0){
                s.emplace(x, y - 1);
                steps[x][y - 1] = steps[x][y] + 1;
            }
            if((y < (n - 1)) && !grid[x][y + 1] && steps[x][y + 1] < 0){
                s.emplace(x, y + 1);
                steps[x][y + 1] = steps[x][y] + 1;
            }
            if(x < (n - 1)){
                if(y > 0 && !grid[x + 1][y - 1] && steps[x + 1][y - 1] < 0){
                    s.emplace(x + 1, y - 1);
                    steps[x + 1][y - 1] = steps[x][y] + 1;
                }
                if(!grid[x + 1][y] && steps[x + 1][y] < 0){
                    s.emplace(x + 1, y);
                    steps[x + 1][y] = steps[x][y] + 1;
                }
                if((y < n - 1) && !grid[x + 1][y + 1] && steps[x + 1][y + 1] < 0){
                    s.emplace(x + 1, y + 1);
                    steps[x + 1][y + 1] = steps[x][y] + 1;
                }
            }
        }
        return steps[n - 1][n - 1];
    }
};

这里的 steps 数组可以完全不需要。