[LeetCode] Single Number 单独的数字

 

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

Input: [2,2,1]
Output: 1

Example 2:

Input: [4,1,2,1,2]
Output: 4

 

这道题给了我们一个非空的整数数组，说是除了一个数字之外所有的数字都正好出现了两次，让我们找出这个只出现一次的数字。题目中让我们在线性的时间复杂度内求解，那么一个非常直接的思路就是使用 HashSet，利用其常数级的查找速度。遍历数组中的每个数字，若当前数字已经在 HashSet 中了，则将 HashSet 中的该数字移除，否则就加入 HashSet。这相当于两两抵消了，最终凡事出现两次的数字都被移除了 HashSet，唯一剩下的那个就是单独数字了，参见代码如下：

 

C++ 解法一：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        unordered_set<int> st;
        for (int num : nums) {
            if (st.count(num)) st.erase(num);
            else st.insert(num);
        }
        return *st.begin();
    }
};

 

Java 解法一：

class Solution {
    public int singleNumber(int[] nums) {
        Set<Integer> st = new HashSet<>();
        for (int num : nums) {
            if (!st.add(num)) st.remove(num);
        }
        return st.iterator().next();
    }
}

 

题目中让我们不使用额外空间来做，本来是一道非常简单的题，但是由于加上了时间复杂度必须是 O(n)，并且空间复杂度为 O(1)，使得不能用排序方法，也不能使用 HashSet 数据结构。那么只能另辟蹊径，需要用位操作 Bit Operation 来解此题，这个解法如果让我想，肯定想不出来，因为谁会想到用逻辑异或来解题呢。逻辑异或的真值表为：

 异或运算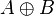的真值表如下：

A	B	⊕
F	F	F
F	T	T
T	F	T
T	T	F

由于数字在计算机是以二进制存储的，每位上都是0或1，如果我们把两个相同的数字异或，0与0 '异或' 是0，1与1 '异或' 也是0，那么我们会得到0。根据这个特点，我们把数组中所有的数字都 '异或' 起来，则每对相同的数字都会得0，然后最后剩下来的数字就是那个只有1次的数字。这个方法确实很赞，但是感觉一般人不会往 '异或' 上想，绝对是为CS专业的同学设计的好题呀，赞一个~~ 

 

C++ 解法二：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = 0;
        for (auto num : nums) res ^= num;
        return res;
    }
};

 

Java 解法二：

class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for (int num : nums) res ^= num;
        return res;
    }
}

 

类似题目：

Single Number III

Single Number II

Missing Number

Find the Difference

Find the Duplicate Number

 

参考资料：

https://leetcode.com/problems/single-number/

https://leetcode.com/problems/single-number/discuss/42997/My-O(n)-solution-using-XOR

 

LeetCode All in One 题目讲解汇总(持续更新中...)