【机器人学：运动规划】快速搜索随机树（RRT---Rapidly-exploring Random Trees）入门及在Matlab中演示

  快速搜索随机树（RRT -Rapidly-ExploringRandom Trees），是一种常见的用于机器人路径（运动）规划的方法，它本质上是一种随机生成的数据结构—树，这种思想自从LaValle在[1]中提出以后已经得到了极大的发展，到现在依然有改进的RRT不断地被提出来。

  机器人的路径（运动）规划的问题被定义为：给定机器人在运动区域的初始位姿 qinit <script type="math/tex" id="MathJax-Element-1921">q_{init} </script>和终点位姿 qgoal <script type="math/tex" id="MathJax-Element-1922">q_{goal}</script>找到一条路径，即一个位姿的连续序列，使得机器人沿该路径能够从初始位姿运动到终点，且不与障碍物发生碰撞。

  对于机械臂来说，一般的运动规划是在大于等于2的多维构型空间（C-Space）中进行的，然而对于初学者来说，可以首先以2维空间中的路径规划为例（例如图1所示的迷宫），掌握一个初步的概念。

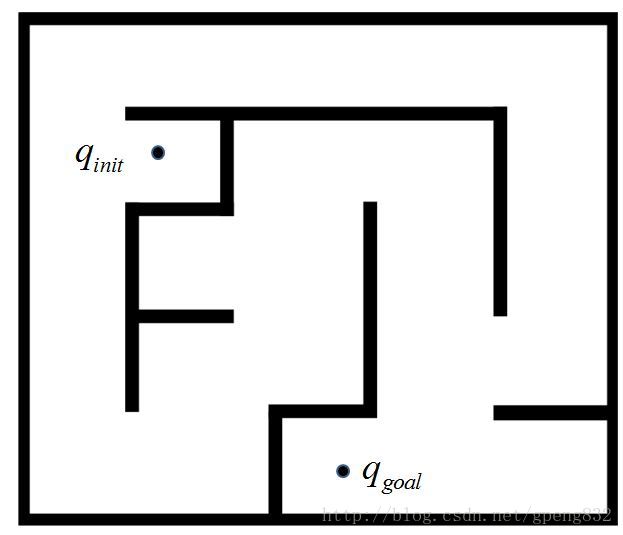
图1 在一个迷宫中设置起点 qinit <script type="math/tex" id="MathJax-Element-1923">q_{init} </script>和终点 qgoal <script type="math/tex" id="MathJax-Element-1924">q_{goal}</script>

  对于机器人运动规划问题，现在有很多开源的代码可供选择学习，例如OMPL，在CSDN上也有人上传了一些RRT的代码，但是大部分是需要积分下载的。为了更加便捷地入门学习RRT的思路，我从Github上找到了一个在Matlab里编写和仿真的代码（源码连接），因为在Matlab中运行程序和可视化相对来说比较简单，所以现在简单介绍一下这个程序，算作是对RRT的初步入门学习。 它的伪代码可以表示成下表：

• 算法：构建RRT
  ————————————————————
• 输入：
  map: 机器人所处环境的信息；
  qinit <script type="math/tex" id="MathJax-Element-1925">q_{init}</script>：机器人的起始位置;
  qgoal <script type="math/tex" id="MathJax-Element-1926">q_{goal}</script>：机器人的终点位置；
  k <script type="math/tex" id="MathJax-Element-1927">k</script>：尝试生成树节点的次数；
  deltaq<script type="math/tex" id="MathJax-Element-1928">deltaq</script>： qnear <script type="math/tex" id="MathJax-Element-1929">q_{near}</script>和 qnew <script type="math/tex" id="MathJax-Element-1930">q_{new}</script>的距离；
  ————————————————————
• 输出
  Vertices <script type="math/tex" id="MathJax-Element-1931">Vertices</script>：RRT的顶点；
  Edges <script type="math/tex" id="MathJax-Element-1932">Edges</script>：RRT的边；
  Path <script type="math/tex" id="MathJax-Element-1933">Path</script>：从 qinit <script type="math/tex" id="MathJax-Element-1934">q_{init}</script>到 qgoal <script type="math/tex" id="MathJax-Element-1935">q_{goal}</script>的原始路径；
  T <script type="math/tex" id="MathJax-Element-1936">T</script>：连接qinit<script type="math/tex" id="MathJax-Element-1937">q_{init}</script>和 qgoal <script type="math/tex" id="MathJax-Element-1938">q_{goal}</script>的树;
  PathSmooth <script type="math/tex" id="MathJax-Element-1939">PathSmooth</script>：连接 qinit <script type="math/tex" id="MathJax-Element-1940">q_{init}</script>和 qgoal <script type="math/tex" id="MathJax-Element-1941">q_{goal}</script>的缩短后的路径；
  ————————————————————
• 1： qrand,qnear,qnew←∅ <script type="math/tex" id="MathJax-Element-1942">q_{rand},q_{near},q_{new}←∅</script>；
  2：for i=1 to k
  3：按一定的概率设置 qrand←qgoal <script type="math/tex" id="MathJax-Element-1943">q_{rand}←q_{goal}</script>或在map中随机生成 qrand <script type="math/tex" id="MathJax-Element-1944">q_{rand}</script>;
  4： qnear←findQNear(qrand,vertices); <script type="math/tex" id="MathJax-Element-1945">q_{near}←findQNear(q_{rand}, vertices);</script>//在 qrand <script type="math/tex" id="MathJax-Element-1946">q_{rand}</script>附近找到距离其最近的 qnear <script type="math/tex" id="MathJax-Element-1947">q_{near}</script>.
  5： qnew←findQNew(qnear,qrand,deltaq); <script type="math/tex" id="MathJax-Element-1948">q_{new}←findQNew(q_{near}, q_{rand}, deltaq);</script>//生成沿 qnear <script type="math/tex" id="MathJax-Element-1949">q_{near}</script>和 qrand <script type="math/tex" id="MathJax-Element-1950">q_{rand}</script>方向上，距 qnear <script type="math/tex" id="MathJax-Element-1951">q_{near}</script>为 deltaq <script type="math/tex" id="MathJax-Element-1952">deltaq</script>的 qnew <script type="math/tex" id="MathJax-Element-1953">q_{new}</script>；
  6：对 qnew <script type="math/tex" id="MathJax-Element-1954">q_{new}</script>到 qnear <script type="math/tex" id="MathJax-Element-1955">q_{near}</script>做碰撞检测；
  7：if 没有碰撞
  8： Vertices←Vertices∪ <script type="math/tex" id="MathJax-Element-1956">Vertices←Vertices∪</script>{ qnew <script type="math/tex" id="MathJax-Element-1957">q_{new}</script>}；
  9： Edges←Edges∪ <script type="math/tex" id="MathJax-Element-1958">Edges←Edges∪</script>{ qnew,qnear <script type="math/tex" id="MathJax-Element-1959">q_{new},q_{near}</script>}；
  10：if qnew <script type="math/tex" id="MathJax-Element-1960">q_{new}</script>= qgoal <script type="math/tex" id="MathJax-Element-1961">q_{goal}</script> or qnew <script type="math/tex" id="MathJax-Element-1962">q_{new}</script>和 qnear <script type="math/tex" id="MathJax-Element-1963">q_{near}</script>将 qgoal <script type="math/tex" id="MathJax-Element-1964">q_{goal}</script>包围
  11： path←fillSolutionPath(edges,vertices); <script type="math/tex" id="MathJax-Element-1965">path←fillSolutionPath(edges, vertices);</script>//将Edges连接起来，即为生成的路径。
  12：endif
  13：endif
  14：endfor
  15： pathSmooth←smooth(map,path,vertices,delta); <script type="math/tex" id="MathJax-Element-1966">pathSmooth ← smooth(map, path, vertices, delta);</script>//使用贪心算法提取缩短后的路径。
  16：Return T；

  需要注意的是在步骤3中该程序使用的方法是以一定的概率将 qgoal <script type="math/tex" id="MathJax-Element-1967">q_{goal}</script>作为 qrand <script type="math/tex" id="MathJax-Element-1968">q_{rand}</script>，这样可以使树的生长方向偏向终点，这与RRT的原始文献[1]是不同的。步骤5生成 qnew <script type="math/tex" id="MathJax-Element-1969">q_{new}</script>示意图如图2所示。

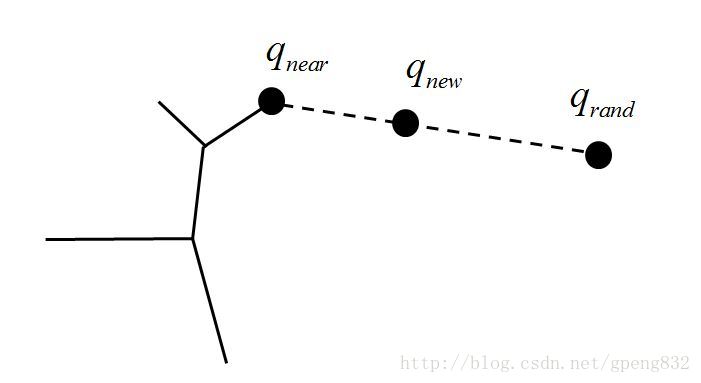
图2 生成 qnew <script type="math/tex" id="MathJax-Element-1970">q_{new}</script>

  对于步骤6的碰撞检测，可将 qnew <script type="math/tex" id="MathJax-Element-1971">q_{new}</script>到 qnear <script type="math/tex" id="MathJax-Element-1972">q_{near}</script>之间的连线插值出若干个点，如图3，对每个点做检测，如果所有的点都不在障碍区域，那么说明两点之间无障碍。

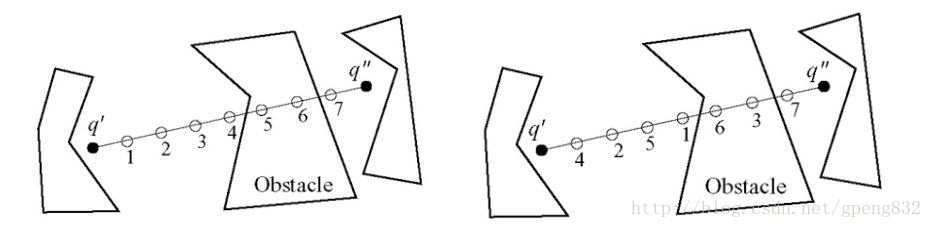
图3 碰撞检测原理

关于最后的一个缩短路径的步骤15（smooth），原理可见下图4，从起点 qinit <script type="math/tex" id="MathJax-Element-1973">q_{init}</script>开始，依次寻找能够能够无碰撞连接终点 qgoal <script type="math/tex" id="MathJax-Element-1974">q_{goal}</script>的顶点，记录此点 q′ <script type="math/tex" id="MathJax-Element-1975">q'</script>，再从起点 qinit <script type="math/tex" id="MathJax-Element-1976">q_{init}</script>开始，以 q′ <script type="math/tex" id="MathJax-Element-1977">q'</script>为终点寻找，直至起点 qinit <script type="math/tex" id="MathJax-Element-1978">q_{init}</script>和 q′ <script type="math/tex" id="MathJax-Element-1979">q'</script>能够无碰撞连接，将所有的 q′ <script type="math/tex" id="MathJax-Element-1980">q'</script>点连接后就得出了缩短后的路径（PathSmooth）。

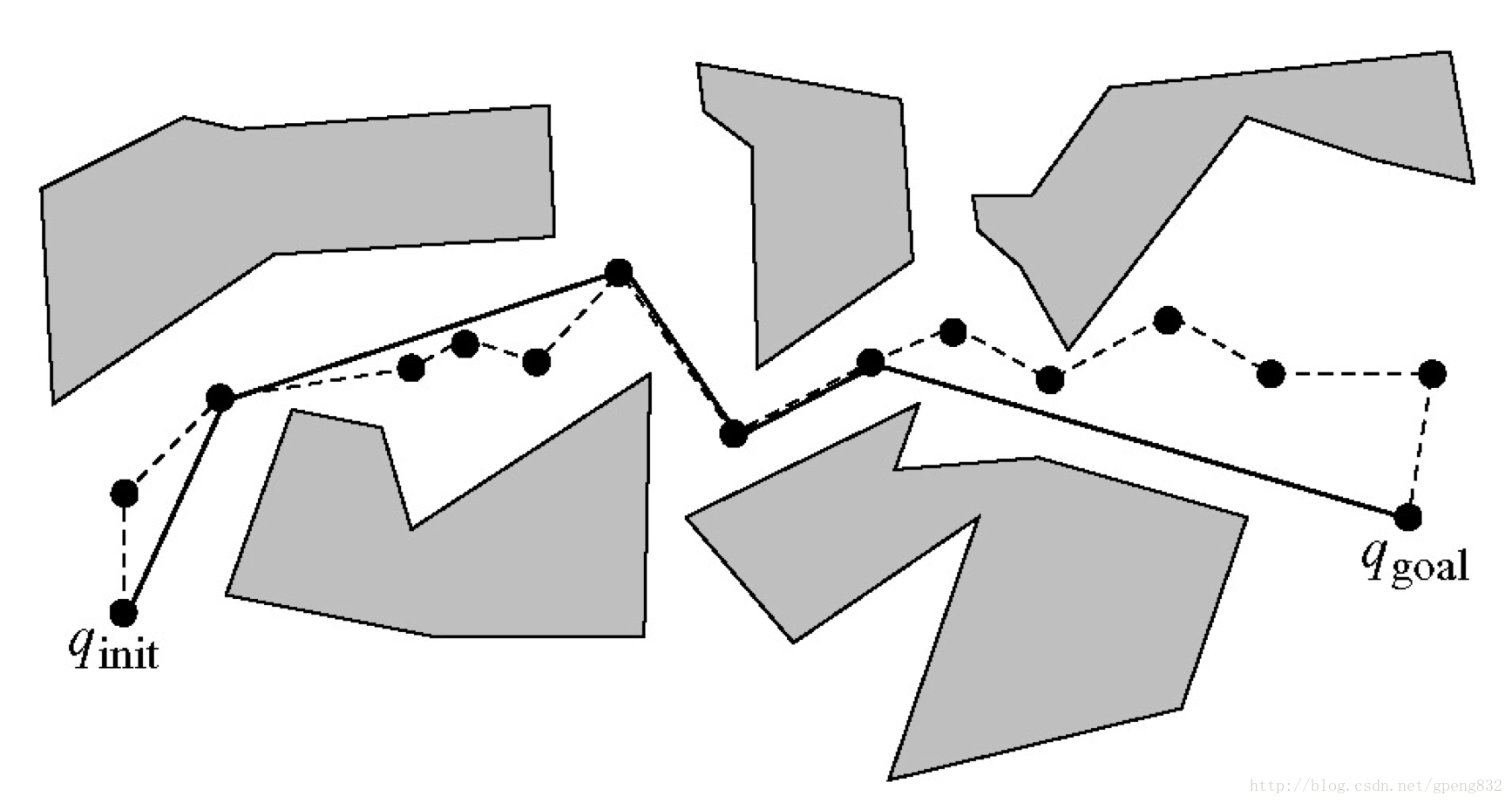
图4 缩短路径的原理

  运行程序之后得到的效果如图5所示，其中红色的路径为原始路径，黑色的路径为缩短（Smooth）后的路径。

图5 运动规划效果

[1]LaValle, S.M., Rapidly-exploring random trees: A new tool for path planning. 1998.
[2]https://github.com/emreozanalkan/RRT