浅谈 fhq-treap —— 或是 Splay 的不二选择?
本文章同步发布至 浅谈 fhq-treap —— 或是 Splay 的不二选择?
参考文献
一、从 BST 谈起
BST 的意思是二叉搜索树,它满足对于所有子树的根节点 \(x\),满足 \(v_{rson} > v_x > v_{lson}\),也就是说,它的中序遍历为一个有序的序列。
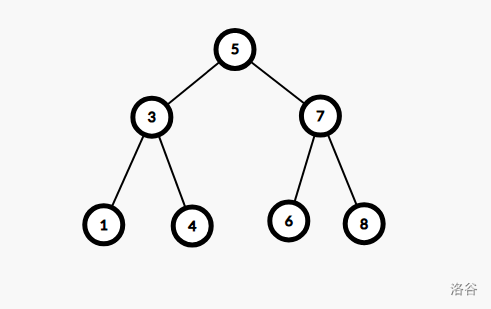
这就是一个 BST,其的中序遍历为 1 3 4 5 6 7 8。
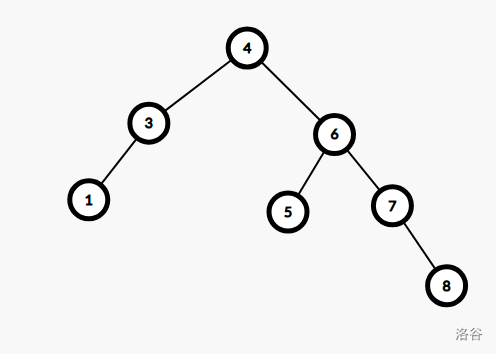
BST 的实现很简单,但由于它的结构不稳定,如上面两张图都是同一个中序遍历,所以会被构造数据卡到 \(O(n)\),但随机数据下仍然为 \(O(\log_2n)\)。
二、关于 treap
treap 上的每一个点有两个值:权值和键值。
- 权值:我们采用 BST 进行维护,使得 \(v_{rson} > v_x > v_{lson}\)。
- 键值:我们随机化键值,然后采用小根堆维护键值,使得 \(g_x < g_{lson},g_{rson}\)。
为什么这棵树的结构是一定的?我们发现 treap 的根节点的键值一定最小,也就是我们的根节点确定了。
此时我们左右两棵子树的权值范围确定了,再根据键值的限制,左右儿子也会确定下来,同理,这颗树也会确定下来。
确定好结构后,我们的 treap 就很好实现了,treap 分为有旋和无旋两种,有旋就是 Splay 等,这里我们将以 fhq-treap 代表的无旋树。
二-ex、关于复杂度
对于权值我们是无法控制的,但对于键值,根据随机化我们的 Heap 高度是 \(\log_2n\),也就是这颗树的高度被 Heap 所限,为 \(\log_2n\),此时的操作复杂度就为 \(O(\log_2n)\)。
三、分裂与合并
fhq-treap 的优点是编写简单,可以实现很多操作,但缺点是需要利用多次分裂与合并操作来进行维护,常数大。
1. 分裂
我们的分裂操作是将权值小于等于 \(x\) 的树从原树上分裂下来,将一颗 \([l,r]\) 范围内的树变为 \([l,x]\) 与 \([x+1,r]\),将一颗 treap 分裂为两颗 treap。
由于 treap 的性质,我们发现分裂后的两颗 treap 的结构也是一定的!
我们来思考如何分裂:
-
对于一棵以 \(u\) 为根的子树,根据 BST 的特点,我们发现若 \(u\) 的左儿子 \(u_{lson}\) 权值 \(val \le x\),那么它的左子树一定也小于 x,此时我们可以把这颗树先分离出来(以 \(x \le 5\) 为例):
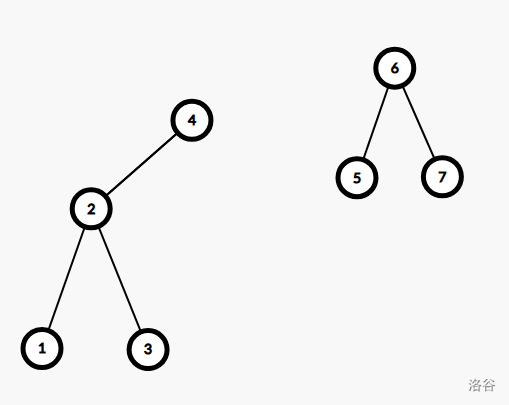
-
对于右子树的操作和左子树一样,但是对于右儿子的权值 \(\le x\),我们只将右儿子与其的左子树加入新树,而右儿子的右子树需要再次递归判断。
-
对于左儿子的权值 \(\ge x\),我们需要递归它左儿子的左子树,对于右儿子也一样。
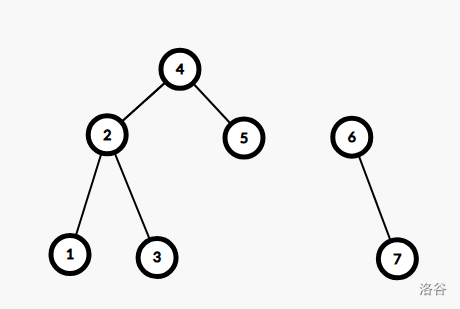
代码实现:
void split(int x,int k,int &l,int &r) {//x 为根,k 为分裂的范围,l 为分裂的左子树,r 为分裂的右子树
if(x == 0) { //树为空
l = r = 0;
return ;
}
if(a[x].val <= k) { //情况 1,左子树已经枚举完了,递归右子树
l = x;
split(a[x].r,k,a[x].r,r);
}
else {//情况 2,左儿子的权值 > k,需要递归左儿子的左子树
r = x;
split(a[x].l,k,l,a[x].l);
}
pushdown(x);//需要更新深度,为 a[x].siz = a[a[x].l].siz + a[a[x].r].siz + 1;
return ;
}
放一个图,帮助大家理解(版权:万万没想到)
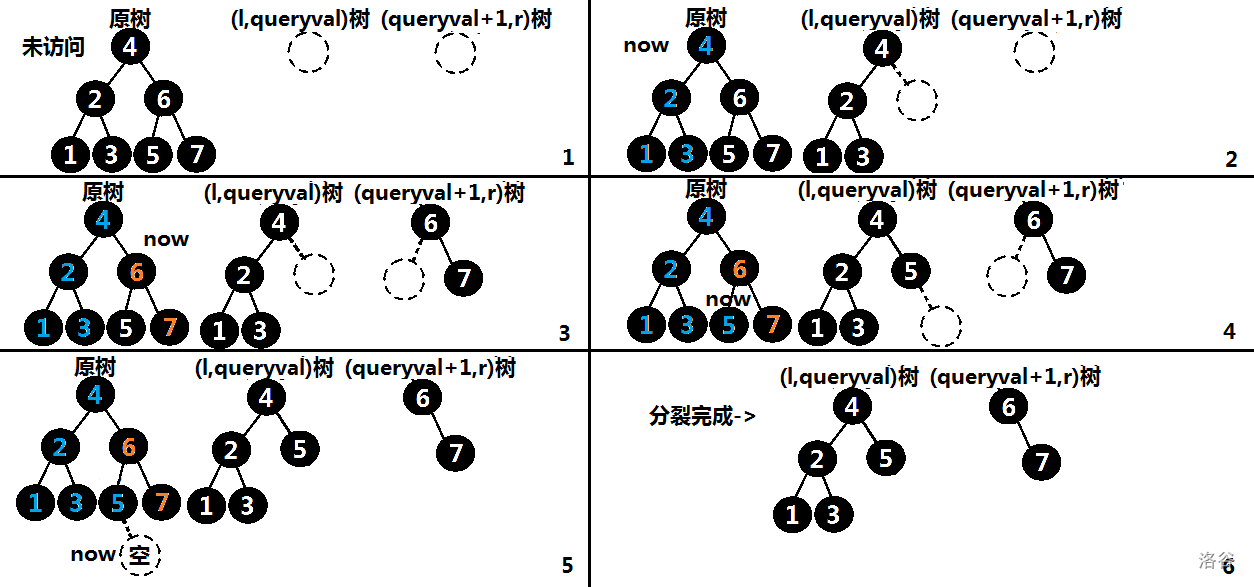
2. 合并
我们合并 \(x\) 和 \(y\) 两棵子树需要用键值,根据 Treap 的特点,我们需要保证根节点的键值最小,故我们需要比较 \(g_x\) 与 \(g_y\),若 \(g_x < g_y\),则递归将 \(x_{rson}\) 与 \(y\) 合并,否则将 \(x\) 与 \(y_{lson}\) 合并。
注意:我们在合并时需要使用 Treap 的特点,所以必须要保证左右两棵子树为 Treap,\(\color{red}{且左子树的权值必须小于右子树!}\)
代码实现:
int merge(int l,int r) {
if(l == 0 || r == 0) return l + r;
if(a[l].key < a[r].key) {
a[l].r = merge(a[l].r,r);
pushdown(l);
return l;
}
else {
a[r].l = merge(l,a[r].l);
pushdown(r);
return r;
}
}
放一个图,帮助大家理解(版权:万万没想到)
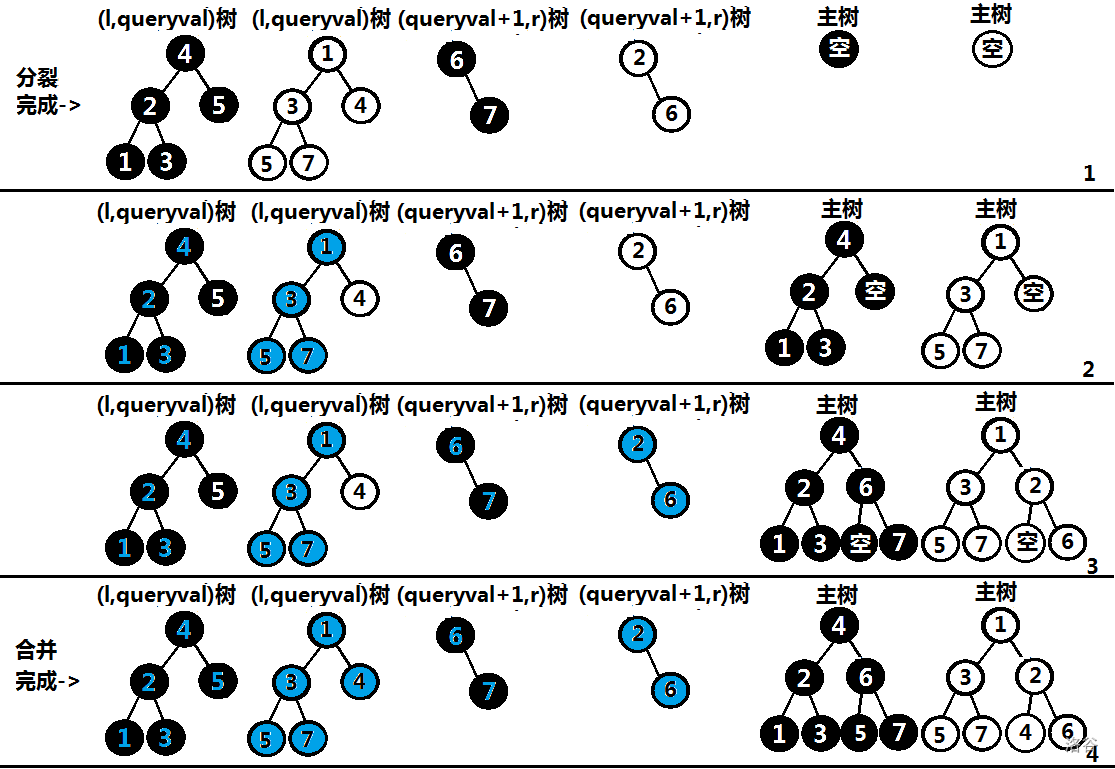
四、插入删除
利用分裂合并我们可以做些什么呢?我们可以维护一个有序序列并支持插入、删除,这是平衡树的基本结构。
1. 插入
-
将 \(\le x\) 的元素分裂;
-
添加新元素 \(x\);
-
先合并权值较小的子树与 \(x\),在合并剩下的子树。
由于合并只能把左子树权值小于右子树的合并,所以只能按这样的顺序排列。
代码实现:
int insert(int x) {
int l,r;
split(root,x,l,r);
newnode(x);
root = merge(merge(l,siz),r);
return siz;
}
2. 删除
I.全部删除
先使用分裂,将所有 \(=x\) 的数找出来,将它分成 \([l,x_l-1],[x_l,x_r],[x_r+1,r]\),然后合并 \([l,x_l-1],[x_r+1,r]\),即可删除
代码实现:
int del_all(int x) {
int l,r,m;
split(root,x,l,r);//先分离 1~x
split(l,x - 1,l,m);//在分离 1~x-1,剩下的为x区间
root = merge(l,r);
return root;
}
II.单个删除
注意到我们需要删除 \([x_l,x_r]\) 中的一个元素,我们只需要把这棵树的左右儿子合并,此时根节点就没有了。
int delone(int x) {
int l,r,m;
split(root,x,l,r);
split(l,x - 1,l,m);
m = merge(a[m].l,a[m].r);//找到 [x_l,x_r]
root = merge(merge(l,m),r);//合并
return root;
}
五、询问排名
1.查找权值为 \(x\) 的排名
很简单,我们分裂所有 \(< x\),将子树 \(+1\) 即为排名。
int getrank(int x) {
int l,r,res;
split(root,x - 1,l,r);
res = a[l].siz + 1;
root = merge(l,r);
return res;
}
2.查找排名为 \(k\) 的数。
我们进行递归操作:
-
若左子树的大小为 \(x+1\),则返回左儿子。
-
若左子树的大小大于 \(x\),则递归左子树。
-
若左子树的大小小于 \(x\),递归右子树中排名为 \(k-x-1\) 的数。
代码实现
int kth(int u,int x) {
if(x == a[a[u].l].siz + 1) return u;
if(x <= a[a[u].l].siz) return kth(a[u].l,x);
else return kth(a[u].r,x - a[a[u].l].siz - 1);
}
六、查询 \(x\) 的前驱后继
1.前驱
我们将 \(1\sim x-1\) 的分离为子树 \(y\),然后找这棵树中排名为 \(y_{siz}\) 的就行了。
2.后继
我们将 \(1\sim x\) 的分离为子树 \(y\),剩下的树为 \(z\),然后找 \(z\) 树中排名为 \(1\) 的就行了。
代码实现:
int pre(int x) {
int l,r,res;
split(root,x - 1,l,r);
res = a[kth(l,a[l].siz)].val;
root = merge(l,r);
return res;
}
int nex(int x) {
int l,r,res;
split(root,x,l,r);
res = a[kth(r,1)].val;
root = merge(l,r);
return res;
}
七、例题
P3369
没什么好说的,直接写代码就可以了。
P6136
同上。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号