DeepSeek-DSA讲解

 1. MQA: Multi-Query Attention

多查询注意力机制 (MQA) 是 Transformer 中使用的传统多头自注意力机制(MHA)的一种变体。在传统的多头注意力机制中，每个注意力头都使用自己的一组查询、键和值，这可能需要大量计算，尤其是在注意力头数量增加的情况下。MQA 通过在多个注意力头之间共享同一组键和值，同时为每个注意力头维护不同的查询，简化了这一过程。这种方法减少了计算和内存开销，而不会显著影响模型的性能。

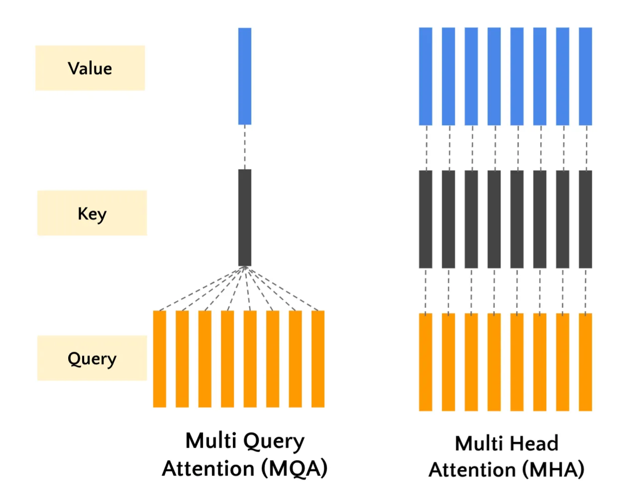
多查询注意力机制的关键概念:

1. 共享键和值：与传统的多头注意力（其中每个头都有自己的键和值）不同，MQA 对所有注意力头使用相同的键和值。
2. 不同查询：MQA 中的每个注意力头仍然使用自己的一组查询，从而允许它从不同方面关注输入序列。
3. 效率：通过共享键和值，MQA 减少了所需的计算量和内存，使其比传统的多头注意力更高效。

多查询注意力机制的好处:

1. 降低计算复杂度：通过共享键和值，MQA 显著减少了所需的操作数量，使其比传统的多头注意力更高效。
2. 更低的内存使用率：MQA 通过存储更少的键和值矩阵来减少内存使用率，这对于处理长序列特别有益。
3. 保持性能：尽管效率有所提高，MQA 仍保持与传统多头注意力机制相媲美的竞争性能，使其成为大规模 NLP 任务的可行选择。

代码实现

import torch
from torch import nn
class MultiQueryAttention(nn.Module):
   def __init__(self, hidden_size, num_heads):
       super(MultiQueryAttention, self).__init__()
       self.num_heads = num_heads
       self.head_dim = hidden_size // num_heads
       self.q_linear = nn.Linear(hidden_size, hidden_size)
       self.k_linear = nn.Linear(hidden_size, self.head_dim)
       self.v_linear = nn.Linear(hidden_size, self.head_dim)
       self.o_linear = nn.Linear(hidden_size, hidden_size)
   def forward(self, hidden_state, attention_mask=None):
       batch_size = hidden_state.size()[0]
       query = self.q_linear(hidden_state)
       key = self.k_linear(hidden_state)
       value = self.v_linear(hidden_state)
       query = self.split_head(query)
       key = self.split_head(key, 1)
       value = self.split_head(value, 1)
       attention_scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim))
       if attention_mask is not None:
           attention_scores += attention_mask * -1e-9
       attention_probs = torch.softmax(attention_scores, dim=-1)
       output = torch.matmul(attention_probs, value)
       output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)
       output = self.o_linear(output)
       return output
   def split_head(self, x, head_num=None):
       batch_size = x.size()[0]
       if head_num is None:
           return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
       else:
           return x.view(batch_size, -1, head_num, self.head_dim).transpose(1, 2)
# 使用示例
hidden_state = torch.rand(32, 10, 512) # 假设输入维度为 (batch_size=32, seq_len=10, hidden_size=512)
attention_mask = None # 可选的注意力掩码
mqa_layer = MultiQueryAttention(hidden_size=512, num_heads=8)
output = mqa_layer(hidden_state, attention_mask)
print(output.shape) # 输出形状应为 (32, 10, 512)

2. GQA：Group Query Attention

组查询注意力 (GQA) 是对 Transformer 中使用的传统多头自注意力机制和多查询注意力机制的折中。在标准多头自注意力中，每个注意力头独立处理整个序列。这种方法虽然功能强大，但计算成本高昂，尤其是对于长序列。而MQA虽然通过在多个注意力头之间共享同一组键和值简化了这一过程，但其简化也不可避免的带来了一些精度的损失。GQA 通过将查询分组在一起来解决此问题，从而降低了计算复杂性，而不会显著影响性能。

组查询注意力机制的关键概念:

1. 分组查询：在 GQA 中，查询根据其相似性或其他标准分组。这允许模型在类似的查询之间共享计算，从而减少所需的总体操作数量。
2. 共享键和值表示：GQA 不会为每个查询计算单独的键和值表示，而是为每个组计算共享键和值表示。这进一步减少了计算负载和内存使用量。
3. 高效计算：通过分组查询和共享计算，GQA 可以更高效地处理更长的序列，使其适合需要处理大量文本或数据的任务。

实际上，MHA和MQA都可以看作是GQA的特殊情况：

• 当组数 g 与 头数 head 相等时，GQA = MHA。
• 当组数 g 为 1 时，GQA = MQA。

大家如果对卷积算法比较熟悉的话，MHA, MQA, GQA 的关系与卷积，逐通道卷积，组卷积的关系是一致的。

代码实现

import torch
import torch.nn as nn
class GroupedQueryAttention(nn.Module):
   def __init__(self, hidden_size, num_heads, group_num):
       super(GroupedQueryAttention, self).__init__()
       self.num_heads = num_heads
       self.head_dim = hidden_size // num_heads
       self.group_num = group_num
       self.q_linear = nn.Linear(hidden_size, hidden_size)
       self.k_linear = nn.Linear(hidden_size, self.group_num * self.head_dim)
       self.v_linear = nn.Linear(hidden_size, self.group_num * self.head_dim)
       self.o_linear = nn.Linear(hidden_size, hidden_size)
   def forward(self, hidden_state, attention_mask=None):
       batch_size = hidden_state.size()[0]
       query = self.q_linear(hidden_state)
       key = self.k_linear(hidden_state)
       value = self.v_linear(hidden_state)
       query = self.split_head(query)
       key = self.split_head(key, self.group_num)
       value = self.split_head(value, self.group_num)
       attention_scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim))
       if attention_mask is not None:
           attention_scores += attention_mask * -1e-9
       attention_probs = torch.softmax(attention_scores, dim=-1)
       output = torch.matmul(attention_probs, value)
       output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)
       output = self.o_linear(output)
       return output
   def split_head(self, x, group_num=None):
       batch_size = x.size()[0]
       if group_num is None:
           return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
       x = x.view(batch_size, -1, group_num, self.head_dim).transpose(1, 2)
       x = x[:, :, None, :, :].expand(batch_size, group_num, self.num_heads // group_num, -1, -1).reshape(batch_size, -1, -1)
       return x

3. MLA： Multi Head Latent Attention

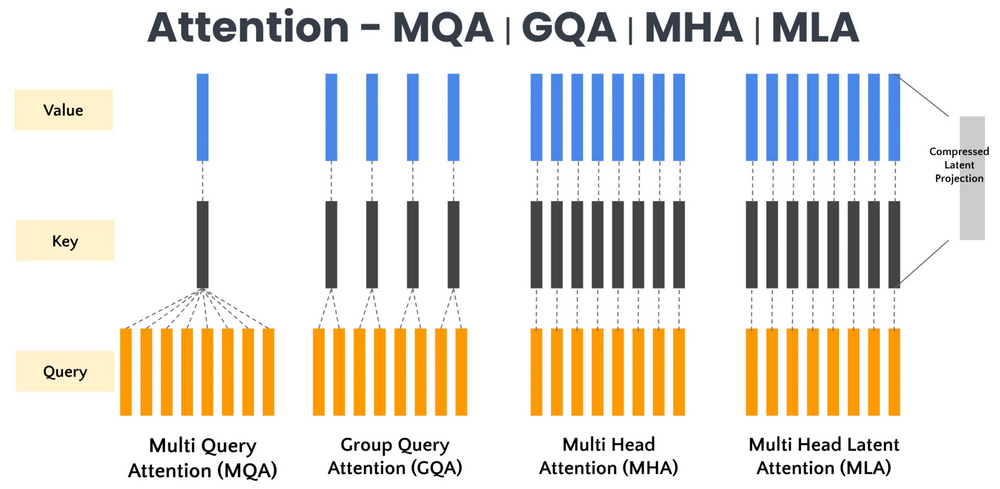
多头潜在注意力 (MLA) 将潜在特征表示纳入注意力机制，以降低计算复杂度并改善上下文表示。MLA的核心是对KV进行压缩后，再送入标准的MHA算法中，用一个更短的k，v向量来进行计算，进而减少KV Cache的大小。

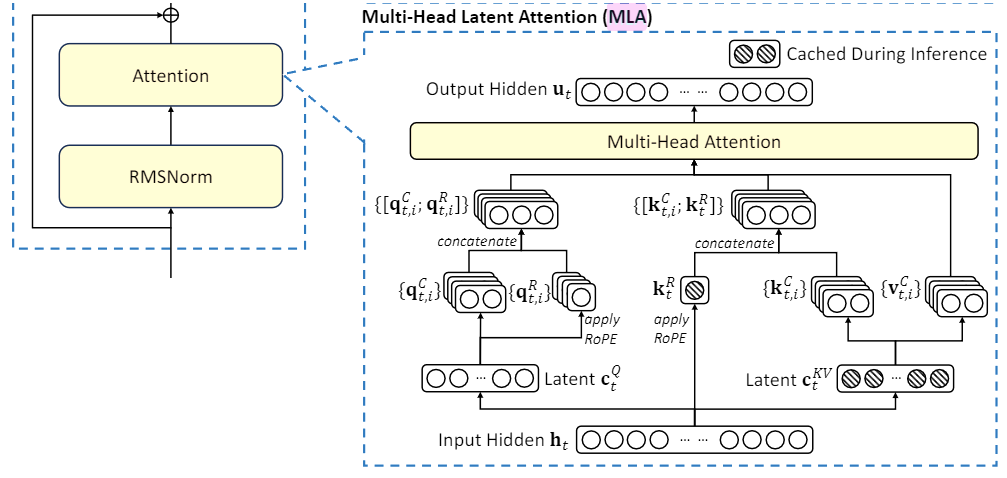
上图中的公式描述了多头注意力机制（Multi-Head Attention, MHA）中潜在向量（latent vectors）的计算过程。以下是对这些公式的逐步解读：

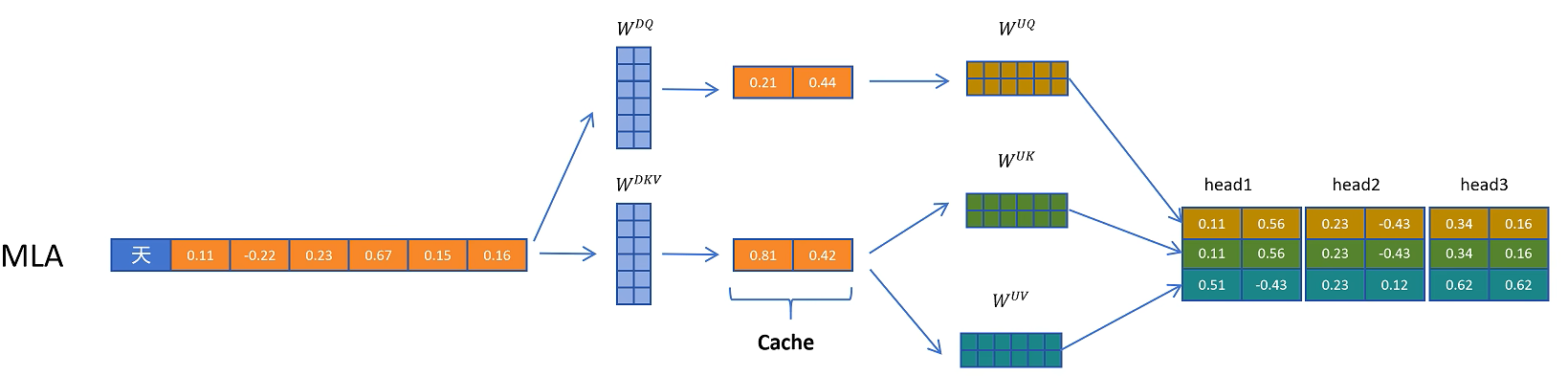
它的原理也很简单，就是对token的特征向量，通过一个参数矩阵进行压缩转换，这个参数我们把它叫做W_dkv，d就是down的意思，表示向下压缩，kv就是K和V向量的意思。比如这里原来的特征维度是6，经过W_dkv压缩到了2维，然后我们只需要缓存这个2维的KV向量，在进行计算时需要用到真实的K和V向量，再从KV压缩向量，通过2个解压矩阵转换为原来的维度就可以了。

把KV压缩向量进行解压，投影到实际K向量的参数矩阵叫做W_uk,u是up的意思，表示向上升维，k表示K向量。同理对V向量进行解压的升维的参数矩阵叫做W_uv.

这时我们可以比较一下原始MHA的KV Cache的缓存量以及MQA的缓存量

 

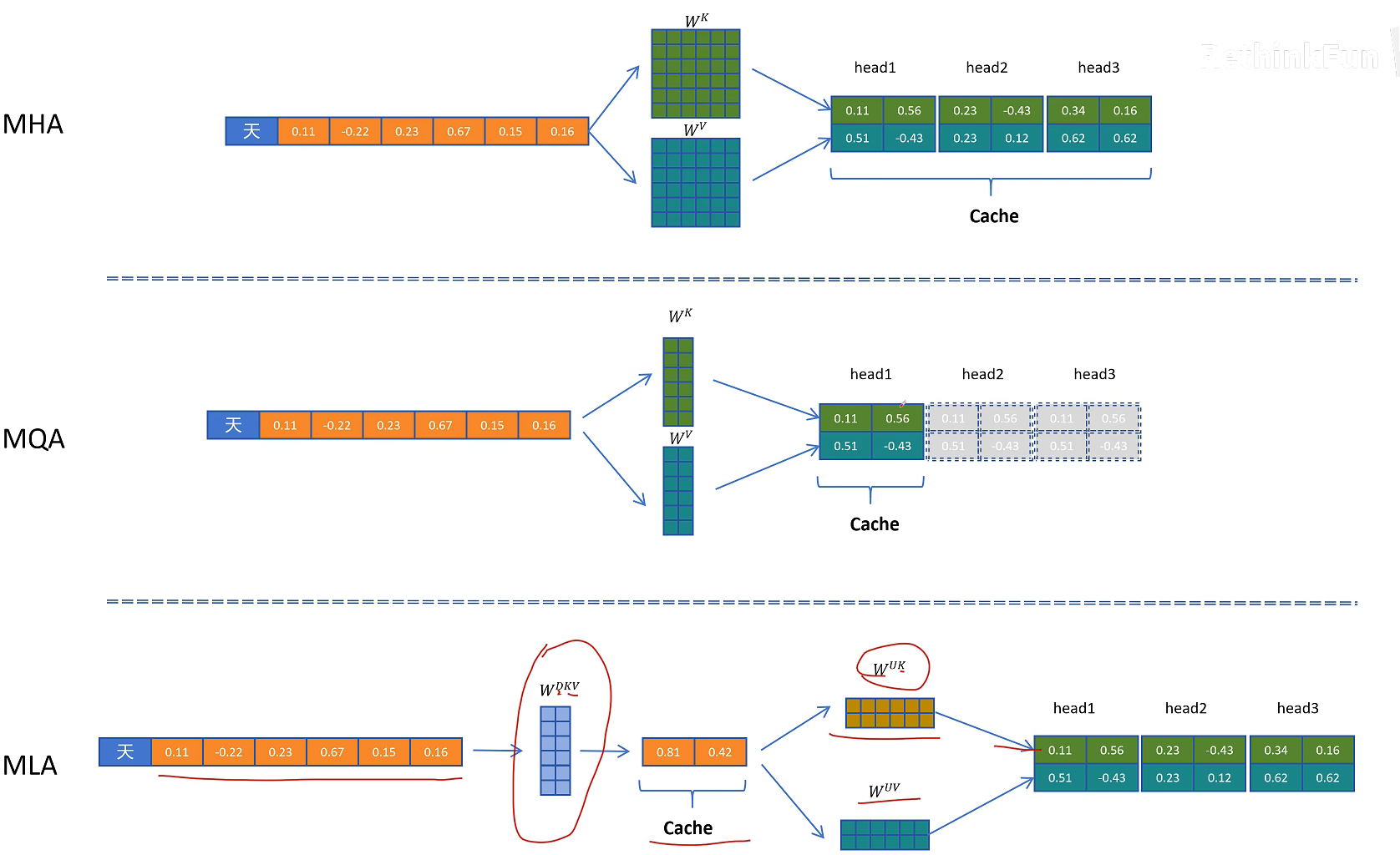
 MLA确实能减少KV Cacha的缓存量，但是会影响模型的效果吗？DeepSeek同样进行了实验来验证。结果惊喜的发现，MLA的模型效果比MHA还要好。所以MLA相比标准的MHA不仅KV Cacha大幅减小，而且意想不到的是模型效果还有提升。

 这一切都非常不错，但是KV Cache的本意是什么呢？它是为了减少推理时对之前token的KV向量的计算而产生的，MLA因为缓存了压缩的KV Cache而减小了显存占用，但是在取出缓存后K和V不能直接使用，还是要经过解压计算才可以，这不是在推理时又引入了解压这个额外的计算吗？这和KV Cache的初衷是相悖的。

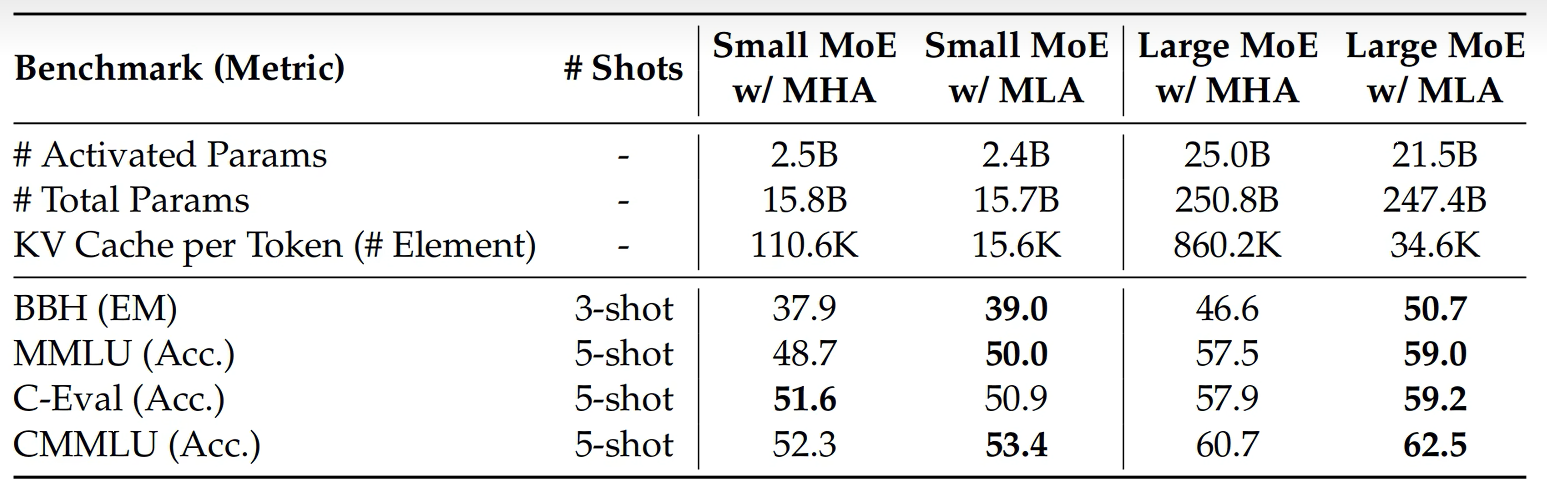
我们看一下KV Cache的推理过程，标准的MHA对于当前的token计算QKV，然后缓存K和V向量，对于之前的token，直接从缓存中取出K和V向量就可以，然后进行Attention的计算。

但是MLA对于当前token的计算，Q的计算不变，但是在K和V的计算时，先通过W_dkv参数矩阵进行压缩，然后生成压缩的KV的隐特征C_kv,并将C_kv缓存在KV Cache里。KV向量通过将KV的压缩隐特征C_kv分别与解压参数矩阵W_uk和W_uv进行相乘，得到当前token的K和V向量。对于之前的token，则从KV Cache里取出压缩的隐特征向量C_kv，然后经过K和V向量的解压参数矩阵投影，得到可以计算的K和V向量。

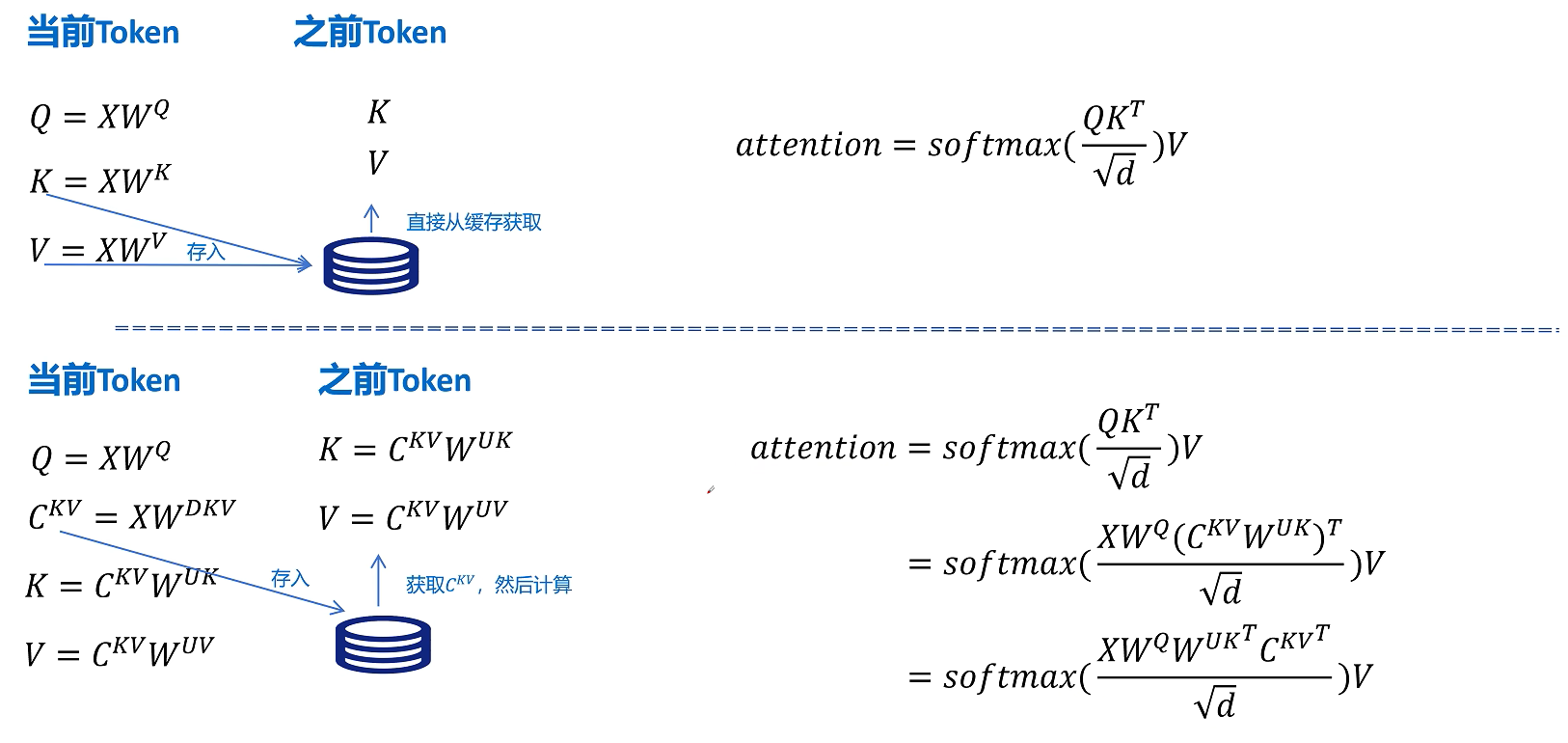
 所以进行注意力计算时它的公式是这样的，我们主要关注的是这里的Q和K_T,代入Q=X*W_q, K=C_kv * W_uk,其中W_q * W_uk可以进行融合，这个融合可以在推理之前计算好，这样在推理时就不用额外对K的解压计算了，这样我们通过矩阵相乘的结合律对矩阵进行提前的融合，就可以规避MLA引入推理时因解压隐特征带来的额外计算了

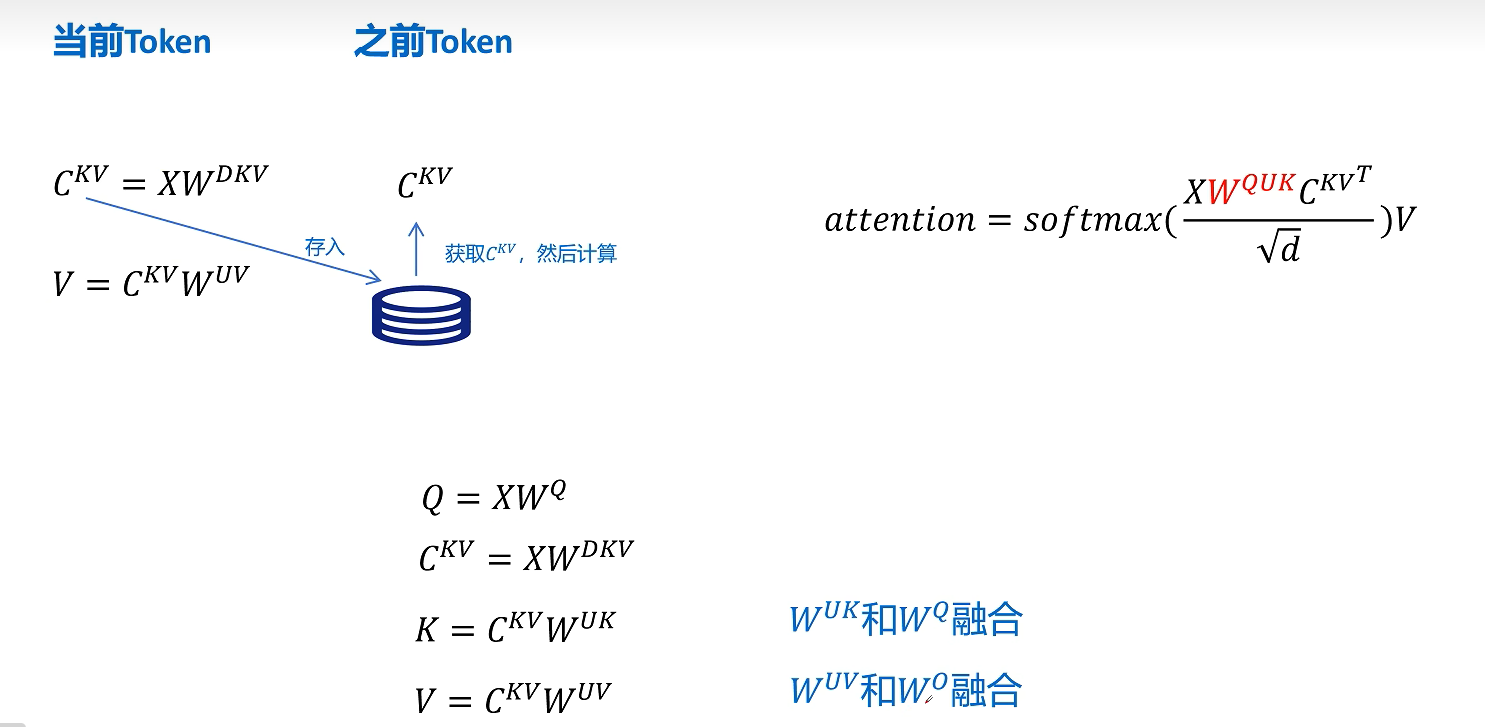
 刚才我们详细看了W_uk可以和W_q进行融合，同样对于V向量进行解压的W_uv也可以和W_o进行融合。

 MLA除了对K和V向量进行压缩外，对Q向量也进行了压缩，这样的好处是降低了参数量，而且可以提高模型的性能，可以看到这里通过W_dq对Q向量进行了压缩，通过W_uq对Q向量进行解压，但是Q的隐向量不需要缓存，只需要缓存KV公用的KV压缩隐向量即可。

 刚才我们一直没有讨论为止编码，确切的说是旋转位置编码RoPE，现在旋转位置编码RoPE已经是大模型默认的位置编码方式了，我们知道旋转位置编码需要对每一层的Q和K向量进行旋转。而且根据token位置的不同，旋转矩阵的参数也不同，这里以第i个token的Q向量和第j个token的K向量进行点积运算为例。如果不考虑旋转位置编码，就是之前所说的W_uk可以和W_q进行融合。但是如果考虑旋转矩阵呢？因为不同位置的旋转矩阵不同，这里我们用R_i和R_j表示，可以发现如果增加了旋转矩阵，它就出现在了W_q和W_uk之间，而且因为R_i和R_j和位置相关，它不能和这两个矩阵进行融合，所以它破坏了之前想到的推理时矩阵提前融合的方案。

 DeepSeek最终想到了一个解决方案，就是给Q和K向量额外增加一些维度来表示位置信息。对于Q向量，它通过W_qr为每一个头生成一些原始特征，这里q代表Q向量，r代表旋转位置编码。

 然后通过旋转位置编码增加位置信息。

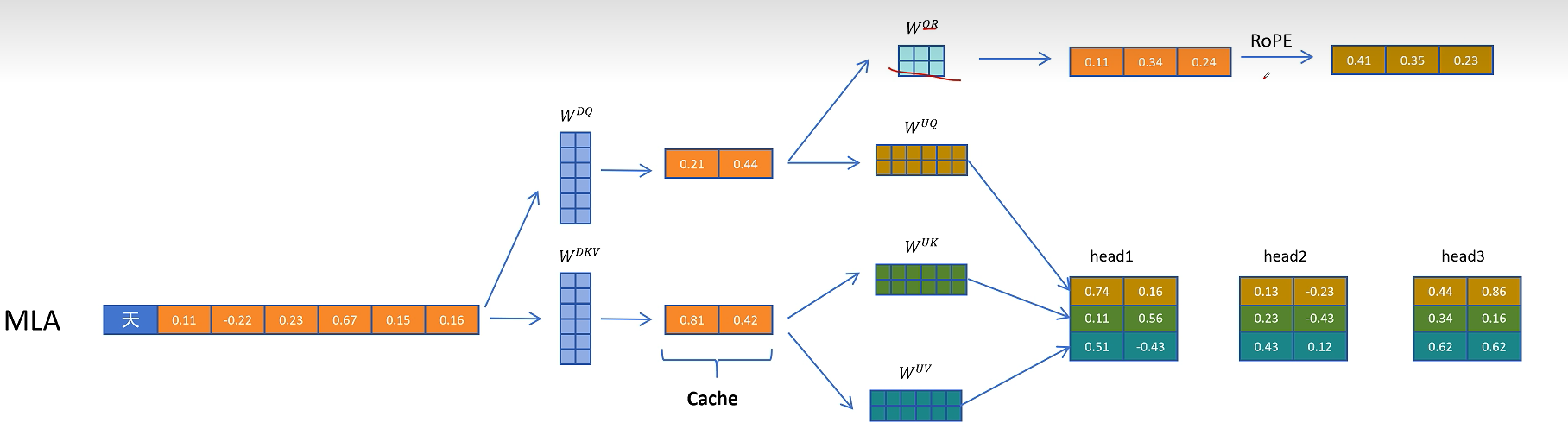
 再把生成带有位置信息的特征拼接到每个注意力头的Q向量。

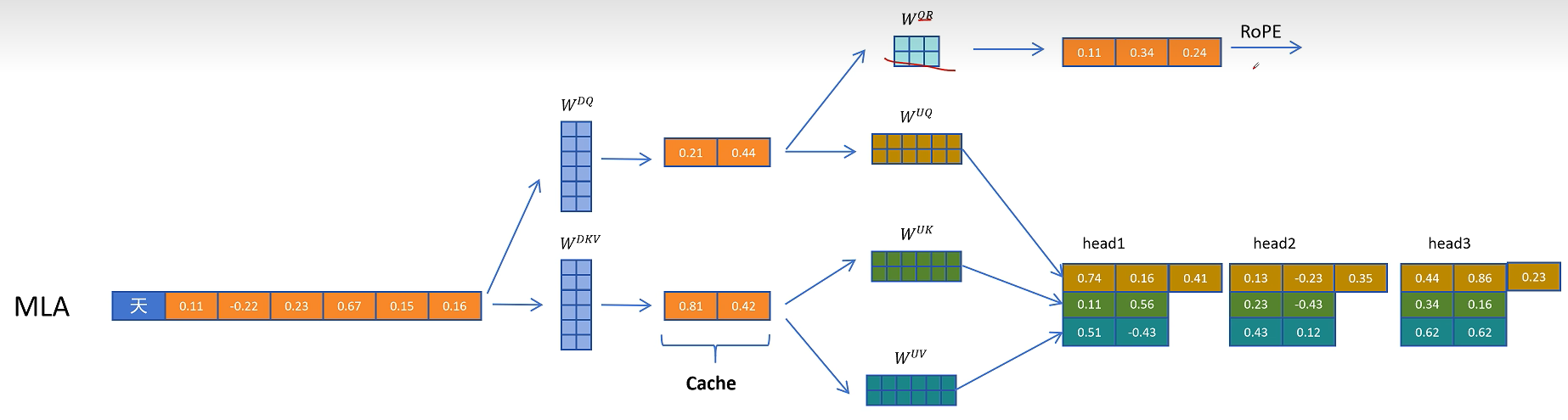
 对于K向量，通过W_kr矩阵生成一个头的共享特征，通过旋转位置编码增加位置信息。

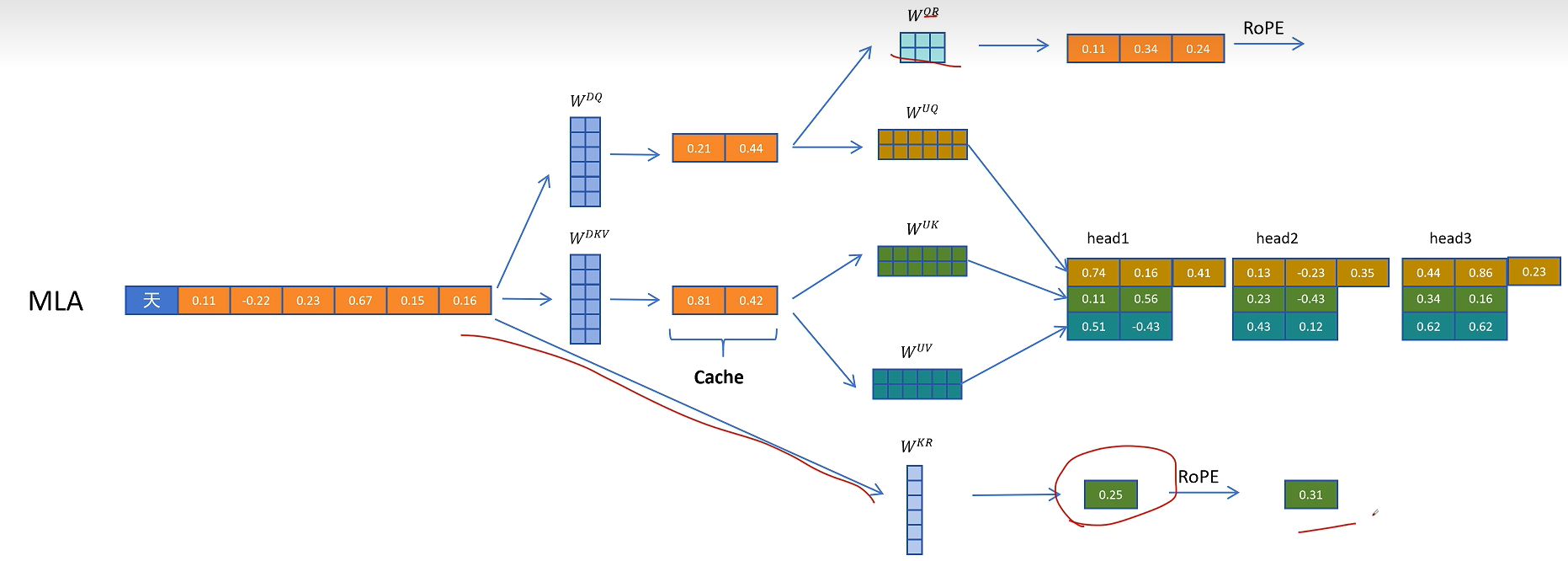
 然后复制到多个头共享位置信息。

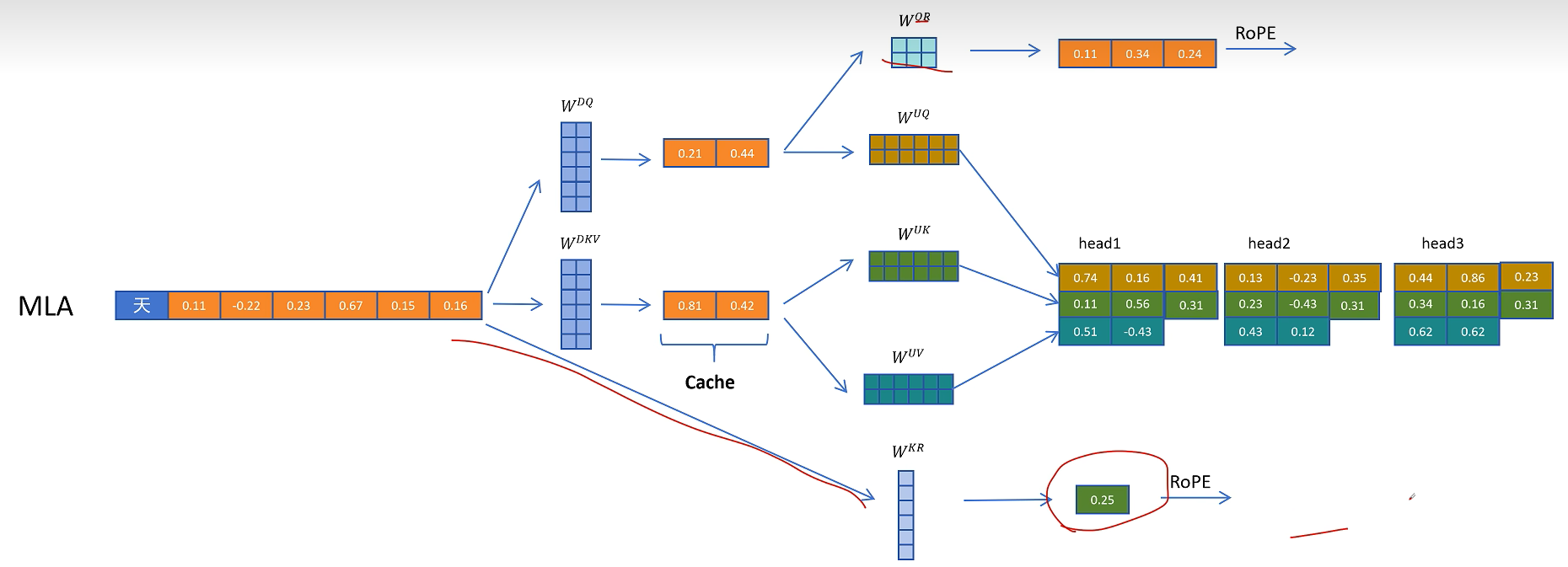
 这里多头共享带位置编码的K向量也需要被缓存，以便在生成带位置信息的K向量时用到。

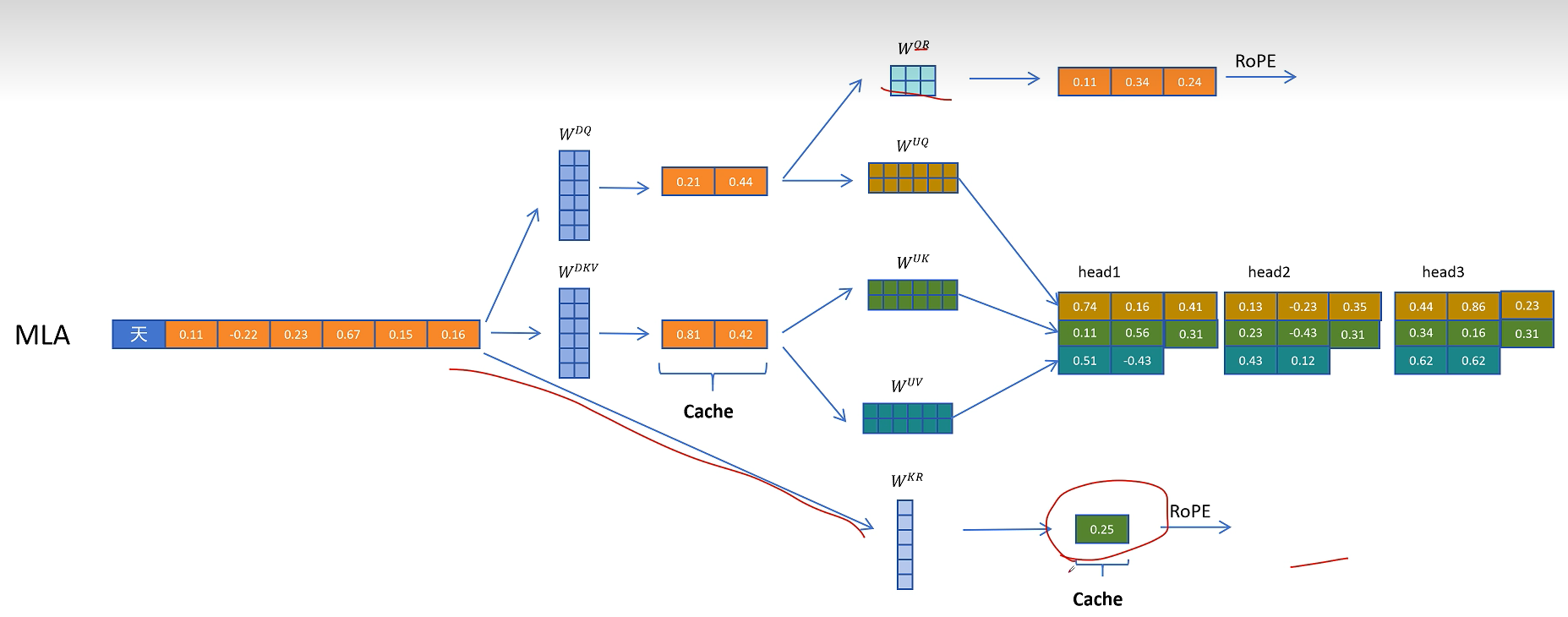
 在推理时不带旋转位置编码的Q和K进行点积运算，这里的计算可以用融合的矩阵来消除解压操作。带旋转位置编码的部分进行点积计算，然后得到的两个值相加，就相当于对拼接了位置信息的完整的Q和K向量进行点积操作的值。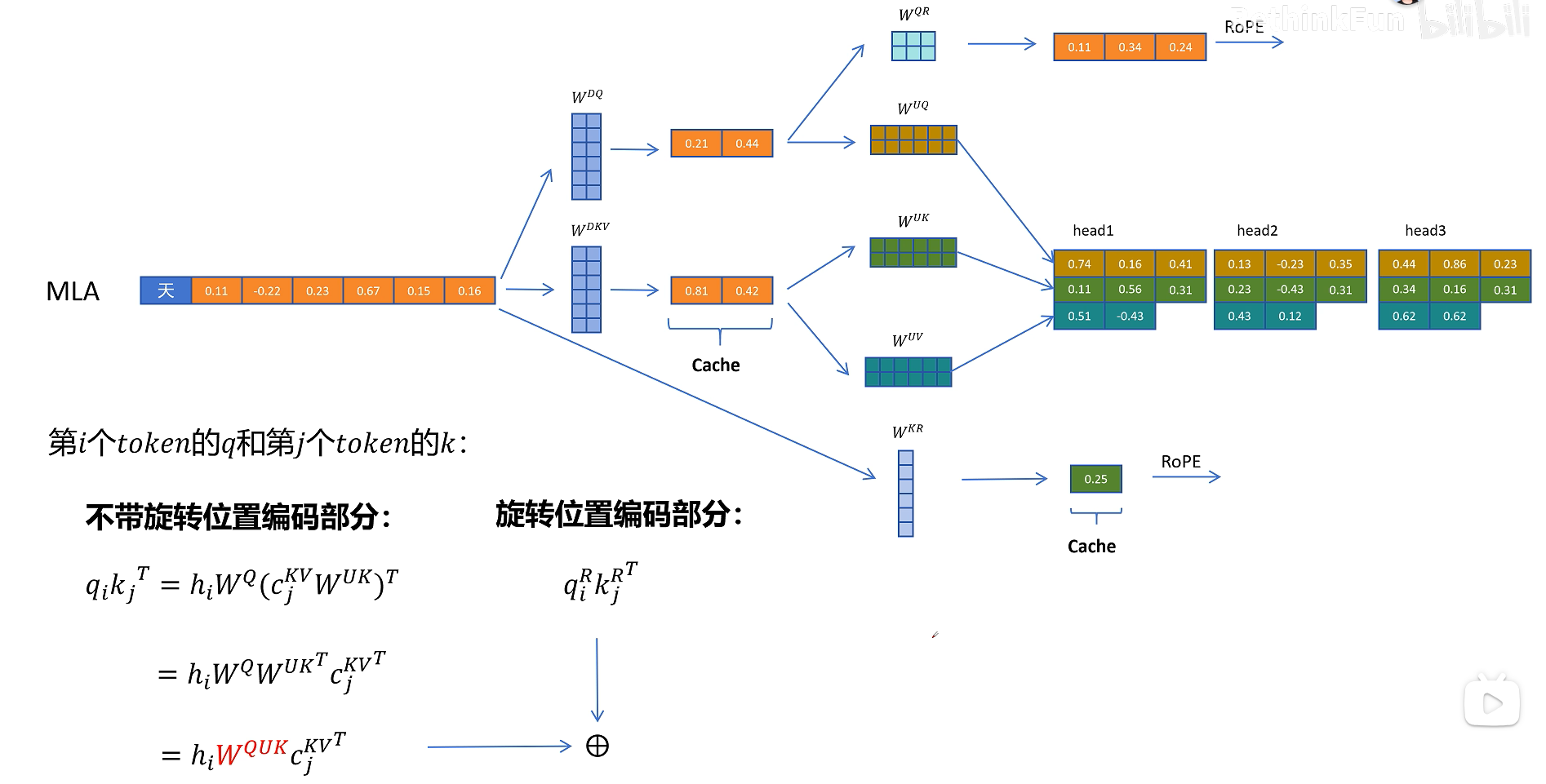 

 到这里终于得到了最终的解决方案，得到了一个既兼容旋转位置编码的压缩KV Cache的方案，同时也可以提升模型的性能。

最后我们来回顾一下论文里面的MLA的图，首先是输入的token特征H，通过它生成压缩的KV特征和压缩的Q向量，然后压缩的KV特征解压为多头的K和V特征，从输入特征H生成多头共享的带旋转位置编码的K_r,再把K_c和K_r合并形成最终带位置编码的K向量。

在看Q向量这边，通过解压生成多头的Q向量，然后从压缩的Q向量生成多头带位置编码的Q_r,然后合并Q_c和Q_r生成最终带位置编码的Q向量。

接着QKV向量进行多头注意力计算。注意图中阴影部分为需要缓存的中间变量。其中只有KV公用的压缩隐特征和K的多头共享的带位置编码的向量需要缓存。

代码实现

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class RMSNorm(nn.Module):
    """Root Mean Square Layer Normalization"""
    def __init__(self, dim, eps=1e-6):
        super().__init__()
        self.dim = dim
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))
        
    def forward(self, x):
        # 计算RMS Norm
        variance = x.pow(2).mean(-1, keepdim=True)
        x = x * torch.rsqrt(variance + self.eps)
        return x * self.weight

def precompute_freqs_cis(dim, max_seq_len, theta=10000.0):
    """预计算位置编码的复数表示"""
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2).float() / dim))
    t = torch.arange(max_seq_len).float()
    freqs = torch.outer(t, freqs)
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
    return freqs_cis

def apply_rotary_emb(x, freqs_cis):
    """应用旋转位置编码"""
    x_complex = torch.view_as_complex(x.float().reshape(*x.shape[:-1], -1, 2))
    freqs_cis = freqs_cis.view(1, x_complex.size(1), 1, x_complex.size(-1))
    x_rotated = torch.view_as_real(x_complex * freqs_cis).flatten(3)
    return x_rotated.type_as(x)

class MLA(nn.Module):
    """多头潜在注意力（Multi-head Latent Attention）"""
    def __init__(self, 
                 dim, 
                 n_heads, 
                 qk_nope_head_dim=128,  # 非位置编码部分的头维度
                 qk_rope_head_dim=64,   # 位置编码部分的头维度
                 v_head_dim=128,        # 值的头维度
                 q_lora_rank=0,         # 查询的低秩投影维度
                 kv_lora_rank=512,      # 键值的低秩投影维度
                 dropout=0.0,
                 attn_impl="naive"):    # 注意力实现方式：naive或absorb
        super().__init__()
        self.dim = dim
        self.n_heads = n_heads
        self.qk_nope_head_dim = qk_nope_head_dim
        self.qk_rope_head_dim = qk_rope_head_dim
        self.qk_head_dim = qk_nope_head_dim + qk_rope_head_dim
        self.v_head_dim = v_head_dim
        self.q_lora_rank = q_lora_rank
        self.kv_lora_rank = kv_lora_rank
        self.attn_impl = attn_impl
        
        # 计算注意力缩放因子
        self.softmax_scale = self.qk_head_dim ** -0.5
        
        # 针对查询的投影层 - 可选使用低秩投影
        if self.q_lora_rank == 0:
            # 直接投影
            self.wq = nn.Linear(dim, n_heads * self.qk_head_dim)
        else:
            # 使用低秩投影 (LoRA)
            self.wq_a = nn.Linear(dim, self.q_lora_rank)
            self.q_norm = RMSNorm(self.q_lora_rank)
            self.wq_b = nn.Linear(self.q_lora_rank, n_heads * self.qk_head_dim)
        
        # 键值使用低秩投影
        self.wkv_a = nn.Linear(dim, self.kv_lora_rank + self.qk_rope_head_dim)
        self.kv_norm = RMSNorm(self.kv_lora_rank)
        self.wkv_b = nn.Linear(self.kv_lora_rank, n_heads * (self.qk_nope_head_dim + self.v_head_dim))
        
        # 输出投影
        self.wo = nn.Linear(n_heads * self.v_head_dim, dim)
        
        # dropout层
        self.dropout = nn.Dropout(dropout)
    
    def forward(self, x, start_pos, freqs_cis, attention_mask=None, max_seq_len=4096):
        batch_size, seq_len, _ = x.shape
        end_pos = start_pos + seq_len
        
        # 生成q向量 - 可选使用低秩投影
        if self.q_lora_rank == 0:
            q = self.wq(x)
        else:
            q = self.wq_b(self.q_norm(self.wq_a(x)))
        
        # 将q分为非位置编码部分和位置编码部分
        q = q.view(batch_size, seq_len, self.n_heads, self.qk_head_dim)
        q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
        
        # 应用旋转位置编码到q_pe
        q_pe = apply_rotary_emb(q_pe, freqs_cis)
        
        # 生成kv向量 - 使用低秩投影
        kv = self.wkv_a(x)
        kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
        k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
        
        # 使用naive方式实现注意力
        if self.attn_impl == "naive":
            # 完整的query向量
            q = torch.cat([q_nope, q_pe], dim=-1)
            
            # 通过低秩投影生成键值
            kv = self.wkv_b(self.kv_norm(kv))
            kv = kv.view(batch_size, seq_len, self.n_heads, self.qk_nope_head_dim + self.v_head_dim)
            k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
            
            # 完整的key向量
            k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_heads, -1)], dim=-1)
            
            # 创建KV缓存
            k_cache = torch.zeros(batch_size, max_seq_len, self.n_heads, self.qk_head_dim, device=x.device, dtype=x.dtype)
            v_cache = torch.zeros(batch_size, max_seq_len, self.n_heads, self.v_head_dim, device=x.device, dtype=x.dtype)
            
            # 更新KV缓存
            k_cache[:, start_pos:end_pos] = k
            v_cache[:, start_pos:end_pos] = v
            
            # 计算注意力分数
            scores = torch.einsum("bshd,bthd->bsht", q, k_cache[:, :end_pos]) * self.softmax_scale
            
        else:  # absorb方式实现注意力
            # 获取wkv_b权重
            wkv_b = self.wkv_b.weight.view(self.n_heads, -1, self.kv_lora_rank)
            
            # 计算q_nope与权重的点积
            q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim])
            
            # 创建KV缓存
            kv_cache = torch.zeros(batch_size, max_seq_len, self.kv_lora_rank, device=x.device, dtype=x.dtype)
            pe_cache = torch.zeros(batch_size, max_seq_len, self.qk_rope_head_dim, device=x.device, dtype=x.dtype)
            
            # 更新KV缓存
            kv_cache[:, start_pos:end_pos] = self.kv_norm(kv)
            pe_cache[:, start_pos:end_pos] = k_pe.squeeze(2)
            
            # 计算注意力分数 - 分别计算非位置编码部分和位置编码部分
            scores = (torch.einsum("bshc,btc->bsht", q_nope, kv_cache[:, :end_pos]) + 
                     torch.einsum("bshr,btr->bsht", q_pe, pe_cache[:, :end_pos])) * self.softmax_scale
        
        # 应用注意力掩码
        if attention_mask is not None:
            scores += attention_mask.unsqueeze(1)
        
        # 注意力权重计算
        attn_weights = F.softmax(scores, dim=-1, dtype=torch.float32).type_as(x)
        attn_weights = self.dropout(attn_weights)
        
        # 计算输出
        if self.attn_impl == "naive":
            output = torch.einsum("bsht,bthd->bshd", attn_weights, v_cache[:, :end_pos])
        else:
            # 先与kv_cache相乘
            output = torch.einsum("bsht,btc->bshc", attn_weights, kv_cache[:, :end_pos])
            # 再与权重相乘生成最终输出
            output = torch.einsum("bshc,hdc->bshd", output, wkv_b[:, -self.v_head_dim:])
        
        # 重塑并投影到原始维度
        output = output.reshape(batch_size, seq_len, -1)
        return self.wo(output)

class MLABlock(nn.Module):
    """包含MLA注意力机制的Transformer块"""
    def __init__(self, 
                 dim=768, 
                 n_heads=12, 
                 qk_nope_head_dim=128, 
                 qk_rope_head_dim=64, 
                 v_head_dim=128,
                 q_lora_rank=0, 
                 kv_lora_rank=512, 
                 mlp_ratio=4, 
                 dropout=0.1, 
                 attn_impl="naive"):
        super().__init__()
        
        # 注意力层
        self.attention = MLA(
            dim=dim,
            n_heads=n_heads,
            qk_nope_head_dim=qk_nope_head_dim,
            qk_rope_head_dim=qk_rope_head_dim,
            v_head_dim=v_head_dim,
            q_lora_rank=q_lora_rank,
            kv_lora_rank=kv_lora_rank,
            dropout=dropout,
            attn_impl=attn_impl
        )
        
        # 前馈网络
        self.mlp = nn.Sequential(
            nn.Linear(dim, int(dim * mlp_ratio)),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(int(dim * mlp_ratio), dim),
            nn.Dropout(dropout)
        )
        
        # 层归一化
        self.norm1 = RMSNorm(dim)
        self.norm2 = RMSNorm(dim)
        
    def forward(self, x, start_pos, freqs_cis, attention_mask=None):
        # 残差连接 + 注意力层
        x = x + self.attention(self.norm1(x), start_pos, freqs_cis, attention_mask)
        # 残差连接 + 前馈网络
        x = x + self.mlp(self.norm2(x))
        return x

 

4. DSA: DeepSeek稀疏注意力机制（ DeepSeek Sparse Attention）

DeepSeek-V3.2-Exp 与上一版本DeepSeek-V3.1-Terminus相比，核心创新在于引入了DeepSeek 稀疏注意力（DSA）。DSA 通过筛选与当前任务高度相关的文本，而非对全部历史 token 进行全量注意力计算，从而显著提升运算效率。

DSA 主要包含两项关键技术：闪电索引器（Lightning Indexer）和细粒度稀疏注意力（Fine-grained Sparse Attention）。整体实现基于 MLA 架构，主要流程可参考 Fig.1:

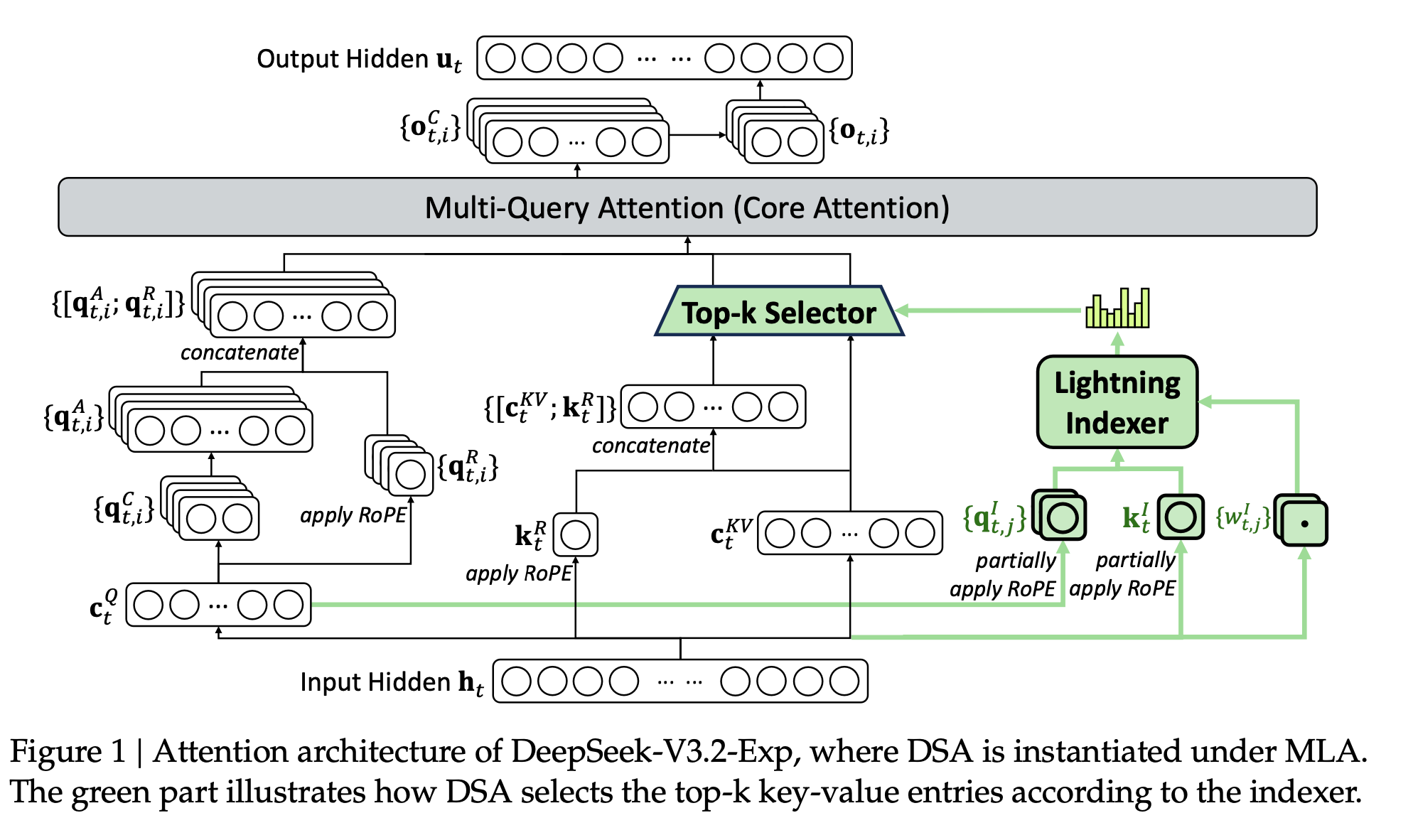
Fig.1 DeepSeek-V3.2-Exp 基于MLA的注意力架构图，其中绿色部分显示了DSA如何根据索引器选择top-k键值条目

1.3 DSA两大核心组件

1.闪电索引器（Lightning Indexer）

闪电索引器负责快速、高效地为每个查询（Query）从海量候选的键（Key）中，识别出最可能相关的 Top-k 个键。闪电索引器的核心目标是以极低的计算开销完成相关键的「海选」。其实现方式如下：

低维投影：将原始高维度的 Query 和 Key 向量，通过一个独立的、可学习的线性层投影到极低的维度（例如128维）。这使得后续的相似度计算变得异常高效。

高效相似度计算：使用低维投影后的向量 qI 和 kI 计算索引分数，这也是索引器的核心作用，也即为每个查询 token（query token）计算「与前文每个 token 的相关性得分」，即索引得分 Iₜ,ₛ，公式如下:

论文指出：选择 ReLU 激活函数的主要考量是其计算上的高吞吐量（throughput），因为与 Softmax 等需要全局归一化的函数相比，ReLU 仅需进行一次简单的阈值操作，计算成本低。

2.细粒度稀疏注意力（Fine-grained Sparse Attention）

基于索引器输出的分数，token选择机制仅保留 Top-k 索引分数对应的键值对（KV），再通过注意力机制计算最终输出 uₜ（仅基于这些筛选后的「关键键值对」计算注意力）。具体工作流程为：

1). 为每个查询token ht计算索引分数{𝐼𝑡,𝑠}

2). 选择 Top-k 索引分数对应的键值条目{𝑐𝑠}

3). 在稀疏选择的键值条目上应用注意力机制，公式如下：

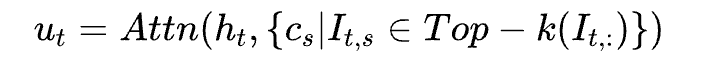
复杂度降低：通过这一机制，核心注意力的计算复杂度从 O(L²) 成功降至 O(L*k)（其中 k 远小于 L），实现了计算量和内存访问的巨大节省。在 DeepSeek-V3.2-Exp 的训练中，k 值设为 2048；也就是说即使处理 128K 长度的文本，每个查询 token 也只需与 2048 个最相似的 token 计算注意力。

这种两阶段设计，既保证了筛选过程的高效率，又确保了最终注意力计算的高精度。

参考: https://www.gnn.club/?p=2729

参考: https://www.bilibili.com/video/BV1BYXRYWEMj

参考: https://www.cnblogs.com/CLTech/p/19134374