为什么词嵌入可以和位置编码相加
一、引言
一个非常朴素的直觉是:
词嵌入是语义,位置编码是词的位置。这两者本身是不同的量纲,就跟身高和体重一样,他们之间有关系,而且我们可以找到他们之间的关系,比如BMI,但是直接把身高(cm)和体重(kg)加起来,就很奇怪了。
所以在回答这个问题之前,我们必须先看看‘位置’这个信息是如何被编码的。
我们要找一个位置信息,要保证两个点
- 位置唯一,这样不会混淆
- 不能过大,不然位置的数值会把词嵌入的信息给淹没或者毫无贡献
二、正余弦编码
$$PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$ $$PE_{(pos,2i + 1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$
- $pos$:词的绝对位置,表示第几个词。
- $i$:代表编码向量的维度索引。这意味着一个位置编码向量 $PE$ 的不同维度上,应用着不同的计算方式。范围是 $d_{\text{model}}/2$ 到 $0$ 之间。
- $d_{\text{model}}$:词嵌入的维度,例如512维。
这个公式的意思可以概括为:用两个有界的函数,通过控制token在不同维度的波长,从而实现高中低维度的数值变化快慢,进而实现向量的不同维度上编码从细到粗粒度的位置信息,共同构成完整的位置表示
三、正余弦编码的特性
3.1 有界性
如果我们直接0,1,2,3,...这样持续的表示位置,很快就会出现位置的值和向量的值差距过大而失去信息。所以我们的位置必须有边界,但是又能同时表示足够的长度。
正弦和余弦函数的值域永远被限制在 [-1, 1] 之间。这就保证了位置编码永远不会因为数值过大而‘淹没’语义信息。它从数学上保证了‘位置’这个信息的‘体重’不会无限增长。
3.2 唯一性和周期性
绝对位置信息
for i in range(8): print(f'{i}的二进制是:{i:>03b}')
0的二进制是:000 1的二进制是:001 2的二进制是:010 3的二进制是:011 4的二进制是:100 5的二进制是:101 6的二进制是:110 7的二进制是:111
P = P[0, :, :].unsqueeze(0).unsqueeze(0) d2l.show_heatmaps(P, xlabel="Col (encoding dim)", ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

3.3 相对位置的表示能力
为什么需要cos,这涉及到这个公式的另一个特性,就是相对位置的表示能力。
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移\(\delta\),位置\(i + \delta\)处的位置编码可以线性投影位置\(i\)处的位置编码来表示。
这种投影的数学解释是,令\(\omega_j = 1/10000^{2j/d}\),对于任何确定的位置偏移\(\delta\),公式中的任何一对\((p_{i,2j}, p_{i,2j+1})\)都可以线性投影到$(p_{i+\delta,2j}, p_{i+\delta,2j+1})$:
$ \begin{bmatrix} \cos(\delta\omega_j) & \sin(\delta\omega_j) \\ -\sin(\delta\omega_j) & \cos(\delta\omega_j) \end{bmatrix} \begin{bmatrix} p_{i,2j} \\ p_{i,2j+1} \end{bmatrix} $
$ = \begin{bmatrix} \cos(\delta\omega_j)\sin(i\omega_j) + \sin(\delta\omega_j)\cos(i\omega_j) \\ -\sin(\delta\omega_j)\sin(i\omega_j) + \cos(\delta\omega_j)\cos(i\omega_j) \end{bmatrix} $
$ = \begin{bmatrix} \sin((i + \delta)\omega_j) \\ \cos((i + \delta)\omega_j) \end{bmatrix} $
$ = \begin{bmatrix} p_{i+\delta,2j} \\ p_{i+\delta,2j+1} \end{bmatrix}, $
\(2 \times 2\)投影矩阵不依赖于任何位置的索引\(i\)。
从一个位置到另一个相对偏移为\(\delta\)的位置,其位置编码向量的变化规律是固定的,与初始绝对位置\((p_{i,2j}, p_{i,2j+1})\)无关。更进一步说,模型已经不需要学习绝对位置\((p_{i,2j}, p_{i,2j+1})\)和\((p_{i+\delta,2j}, p_{i+\delta,2j+1})\)的复杂映射,而只需学习一个统一的、线性的变换规则来识别“相距\(\delta\)个单位”这一相对概念。
四、高维空间和向量特性
从一个简单的例子来看,如果我们有一个数 100。单纯给我100,我是无法知道这个100是从何而来的,就算我知道他只会是2个数相加,那我也无法区分是哪两个数。这两个数可以是1和99,也可以是50和50。这种我们称为标量,是无法严格区分开来的。
但是我们是在高维空间下,每一个token的含义都被分解为了512(或者更高)维度下的向量。向量是有方向的,也就说我们可以分解回去。什么意思呢。比如我有向量[4,3],4表示的是语义,它原始的向量应该是[4,0],3表示的是位置那就是[0,3],这样我们拿到[3,4]的时候,可以轻易的分离语义和位置信息。
也就是说:高维空间提供了信息分离的基础
这可以说的通了。但是这里有两个前提。
- 位置信息有自己的空间
- 位置信息所在的空间和语义空间是近似正交的。
怎么去理解这两个点呢?
语义不是均匀分布在欧式空间中的。也就是说即使我们有一个token叫“人工智能”,它被分解为一个512维度的向量。这个512个维度上的值,也不是均匀分布的。一定有一部分是语义的富集,一些值的语义是稀疏的。这就给了我们的位置信息嵌入到这些为止的可能。
正交就更好理解了。我们能分离语义的前提是,语义和位置的向量应该在不同的方向上的。也就是他们之间本身是互不干扰的。这很好理解,本来就是两个不同的东西。我们唯一需要确认的就是他们是不是近似正交。
训练初期,他们确实不是近似正交的。词嵌入和位置编码在训练阶段初期,必然是会出现混淆,也破坏了语义
我们是通过损失函数和反向传播,不断的去迫使模型把位置的信息放到语义稀疏的维度上。迫使模型逐渐学会分离信息。
但是注意,在训练后的,模型会逐步学会分离两者的关系,在高维空间中形成正交。所以正交性是通过训练实现的。
我们直接看一个辅助性的结论。
4.1 在BERT上测试语义和位置的夹角
上面说的都是理论,如果说的成立,那么我们应该是可以去计算这个结果的。在bert里试一下。
import torch import numpy as np from transformers import BertModel from sklearn.metrics.pairwise import cosine_similarity # 1. 加载模型并提取嵌入向量 model = BertModel.from_pretrained('bert-base-uncased') word_embeddings = model.embeddings.word_embeddings.weight.data.cpu().numpy() pos_embeddings = model.embeddings.position_embeddings.weight.data.cpu().numpy() # 2. 选取部分词向量用于计算 sampled_word_embeddings = word_embeddings[100:1100, :] # 共1000个词向量(1100-100) # 3. 计算余弦相似度矩阵(shape: [1000, 512],1000个词 × 512个位置) similarity_matrix = cosine_similarity(sampled_word_embeddings, pos_embeddings) # 4. angle_matrix:每个词-位置对的夹角(角度),shape与similarity_matrix一致 [1000, 512] # 步骤:先通过反余弦算弧度,再转角度(×180/π) angle_matrix = np.arccos(similarity_matrix) * (180 / np.pi) # 5. all_similarities:所有词-位置对的余弦相似度,展平为1维数组(1000×512=512000个元素) all_similarities = similarity_matrix.flatten() # 6. all_angles:所有词-位置对的夹角(角度),展平为1维数组(与all_similarities长度一致) all_angles = angle_matrix.flatten() # ------------------------------------------------------------------------------ # 后续打印代码可正常运行 print(f"\n========== 相似度统计 ==========") print(f" 均值: {np.mean(all_similarities):.6f}") print(f" 标准差: {np.std(all_similarities):.6f}") print(f" 绝对值均值: {np.mean(np.abs(all_similarities)):.6f}") print(f"\n========== 角度统计 ==========") print(f" 平均夹角: {np.mean(all_angles):.2f}°") print(f" 夹角标准差: {np.std(all_angles):.2f}°") print(f" 夹角范围: [{np.min(all_angles):.2f}°, {np.max(all_angles):.2f}°]") print(f"\n========== 具体示例分析 ==========") print(f" 第一个词与第一个位置:") print(f" - 相似度: {similarity_matrix[0, 0]:.6f}") print(f" - 夹角: {angle_matrix[0, 0]:.2f}°") print(f"\n 第一个词与第二个位置:") print(f" - 相似度: {similarity_matrix[0, 1]:.6f}") print(f" - 夹角: {angle_matrix[0, 1]:.2f}°") word_idx = 10 pos_idx = 5 print(f"\n 词{word_idx}与位置{pos_idx}:") print(f" - 相似度: {similarity_matrix[word_idx, pos_idx]:.6f}") print(f" - 夹角: {angle_matrix[word_idx, pos_idx]:.2f}°") word_similarities = similarity_matrix[word_idx, :] word_angles = angle_matrix[word_idx, :] print(f"\n 词{word_idx}与所有位置:") print(f" - 相似度范围: {word_similarities.min():.6f} ~ {word_similarities.max():.6f}") print(f" - 夹角范围: {word_angles.min():.2f}° ~ {word_angles.max():.2f}°") pos_similarities = similarity_matrix[:, pos_idx] pos_angles = angle_matrix[:, pos_idx] print(f"\n 位置{pos_idx}与所有词:") print(f" - 相似度范围: {pos_similarities.min():.6f} ~ {pos_similarities.max():.6f}") print(f" - 夹角范围: {pos_angles.min():.2f}° ~ {pos_angles.max():.2f}°")
结果如下:
========== 相似度统计 ========== 均值: -0.009876 标准差: 0.035428 绝对值均值: 0.028139 ========== 角度统计 ========== 平均夹角: 90.57° 夹角标准差: 2.03° 夹角范围: [7.72°, 98.00°] ========== 具体示例分析 ========== 第一个词与第一个位置: - 相似度: 0.018469 - 夹角: 88.94° 第一个词与第二个位置: - 相似度: -0.074933 - 夹角: 94.30° 词10与位置5: - 相似度: -0.025367 - 夹角: 91.45° 词10与所有位置: - 相似度范围: -0.114627 ~ 0.145001 - 夹角范围: 81.66° ~ 96.58° 位置5与所有词: - 相似度范围: -0.082197 ~ 0.070120 - 夹角范围: 85.98° ~ 94.71°
很好,可以说随机取一下,他们都是几乎正交的。可以说实践和理论对上了。
五、Attention和FFN视角下的可解释性
仅仅证明输入端可以相加并且理论上可分是不够的。Transformer的核心是自注意力(Self-Attention)和前馈网络(Feed-Forward Network, FFN)。我们需要理解这两个模块是如何与这些“混合向量”协同工作的。
5.1 Position-wise FFN:位置无关的前馈神经网络
首先看FFN,它的全称是 Position-wise Feed-Forward Network。这里的“Position-wise”是一个关键线索。它意味着同一个FFN(即同一组权重W1, b1, W2, b2)被独立地应用到序列中每一个位置(Position)的向量上。
这说明什么?FFN本身是一个“位置盲”的模块。它不知道自己正在处理的是第3个词的向量还是第30个词的向量。它所做的,只是对输入的单个向量进行一次复杂的非线性变换。
这就带来了一个重要的推论:如果模型需要区分不同位置的词,那么这种区分能力必须来自于输入给FFN的向量本身。因为FFN对所有位置一视同仁,所以向量 H_pos = E_token + P_pos 必须在变换后依然保留着可以区分的语义和位置信息。这从侧面印证了,模型必须在向量内部维持这种信息的正交性或可分离性,否则经过FFN这个“盲处理”后,信息就会彻底混淆。
5.2 Attention 机制:理论上的信息分离能力
之前也写过多头注意力,我们知道多头注意力可以学到不同的内容。那么是否存在一个或者多个头是对位置关系侧重的呢?
针对多头注意力的研究中,论文《Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting》是通过”剪枝“来分析哪些头重要,其中明确功能的就包括:“位置头”。(其他关键头还有句法头和罕见词头)。
Note
虽然许多头表现出明显的专业化倾向,但它们的功能并非绝对单一。一个头可能主要关注位置,但同时也编码了部分语义或句法信息。专业化是一种显著趋势。也就说一个头虽然被称为”位置头“但是依然可能有语法或者句法的部分信息在里面。
当然除了这一个佐证以外,我们还能从数学公式上去进一步论证。
Attention机制是信息交互的核心。一个词的最终表示,是序列中所有其他词表示的加权和。这里的权重,即注意力分数在公式上的表现是这样的:
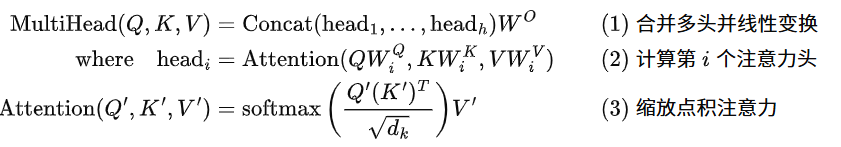
现在,聚焦于注意力分数的核心计算,即 Q'K'^T 这一步,来探究一个头(Head)内部是如何区分语义信息和位置信息的。
我们知道,输入给Transformer的词表示 H 是由词嵌入 E 和位置编码 P 相加得到的(H_i = E_i + P_i)。那么,对于某个特定的头(我们省略头的下标 i 以简化表示),其查询向量 Q_i 和键向量 K_j 的计算如下:
让我们展开这个计算过程:
$$Q_i = H_i * W^Q = (E_i + P_i) * W^Q$$ $$K_j = H_j * W^K = (E_j + P_j) * W^K$$
那么,$Q\_i * K\_j^\intercal$ 就可以分解为四个部分的和:
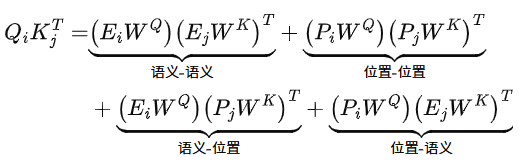
1. 语义-语义:$\left(E_i * W_Q\right) * \left(E_j * W_K\right)$。这部分捕捉纯粹的词义相关性。比如,"苹果"这个词对"公司"和"水果"的注意力就源于此。
2. 位置-位置:$\left(P_i * W_Q\right) * \left(P_j * W_K\right)$。这部分捕捉纯粹的位置关系。例如,模型可能会学到让一个词更关注它前面或后面的词。正余弦编码的线性特性使得 $P_{\text{pos}+k}$ 可以由 $P_{\text{pos}}$ 线性表示,这让模型可以学习相对位置关系。
3. 语义-位置:$\left(E_i * W_Q\right) * \left(P_j * W_K\right)$。这部分捕捉"某个特定词"对"某个特定位置"的偏好。虽然比较少见,但理论上是存在的。
4. 位置-语义:$\left(P_i * W_Q\right) * \left(E_j * W_K\right)$。这部分捕捉"某个特定位置"对"某个特定词"的偏好。例如,在某些任务中,句首的词可能更倾向于关注序列中的动词。
所以这也从数学上部分的回答了,Attention的头,到底在学习什么?是不是能够提取位置关系?
有的头可能主要关注“语义-语义”,成为语义专家;有的头可能主要关注“位置-位置”,成为位置专家
六、结论
到现在,我们可以给出一个结论了,在Transformer架构中,将词嵌入向量与位置编码向量进行逐元素相加是理论上可行的。
核心原因在于高维向量空间的几何特性以及深度学习模型的优化过程。经过训练,模型会学习到将词嵌入所代表的语义信息和位置编码所代表的序列顺序信息,分别映射到高维空间中两个近似正交的子空间内。
这就保证了语义信息和位置信息的可分离。后续的模块中,不论是Attention还是FFN都能正确的提取到给定向量中的语义和位置信息。保证了近乎独立地处理和加权。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号